信息论与编码技术之无失真信源编码小结

目录

前言：

一．信源编码的概念（基本概念，分类，要求，目的）

1.对信源编码的要求：

2.分类

3.信源编码的目的：减小冗余，提高效率

二．定长码

1.信源存在唯一可译定长码的条件

2.定长编码定理（重点：叙述，含义，公式，计算）

四．变长码（重点：特点，树图构造即时码，kraft不等式的证明，变长编码定理的叙述和意义）

1.特点

2.要求

3.kraft不等式

4.变长编码定理

5.变长无失真信源编码定理（香农第一定理）（重点：叙述，含义）

五．哈夫曼编码（重点，简单信源（N次扩展信源）编码，计算​)

1.二元huffman编码

2.n元huffman编码：

六．香农编码，费诺编码（重点：编码，特点）

前言：

四个基本概念：

一个图：维拉图

一个基本原则：获取信息的过程就是减小不确定性的过程

一．信源编码的概念（基本概念，分类，要求，目的）

1.对信源编码的要求：

①非奇异性：分组码是非奇异应是正确译码的必要条件，而非充分条件。

②唯一可译性：

定长码：非奇异码

变长码：非奇异码且其N次扩展码也是非奇异的。

③即时码：（前缀码）

2.分类

3.信源编码的目的：减小冗余，提高效率

①去掉相关性：编码或码序列中各个码符号尽可能相互独立。

②使编码后各码符号出现的概率尽可能相等。

二．定长码

1.信源存在唯一可译定长码的条件

简单信源：

N次扩展信源：

2.定长编码定理（重点：叙述，含义，公式，计算）

离散无记忆信源的N次扩展信源

若

则当N足够大时，必可使译码差错小于（）

若

则当N足够大时，译码差错趋于1。（）

当信源为有记忆信源时：H(S)改为

Pe：是集合出现的概率:

编码速度：

表示编码后，平均每个信源符号所能载荷的最大信息量。

编码效率：

四．变长码（重点：特点，树图构造即时码，kraft不等式的证明，变长编码定理的叙述和意义）

1.特点

在N不大时，就能编出效率很高，且无失真的信源编码。

2.要求

唯一可译码：必须是非奇异的，且N次扩展也是非奇异的。

即时码：构造即时码的方法（树图法）

3.kraft不等式

注意：根据要求构造一个即时码（用树图法），先考虑是否满足kraft不等式？

意义：说明信源符号数，码符号数与码长之间满足什么条件才能构成即时码。

证明：①充分性②必要性（要求掌握kraft不等式的证明）

4.变长编码定理

平均码长

单位：码符号/信源符号。表示每个信源符号平均所需用的码元数。

码率：每个码元符号携带的平均信息量

编码后信道每秒钟传输的信息量

平均码长界定定理：离散无记忆信源的熵为H(S)，则一定存在一种编码方式构成唯一可译码，使其平均码长满足：

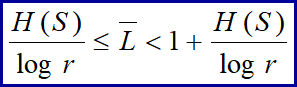
5.变长无失真信源编码定理（香农第一定理）（重点：叙述，含义）

编码速率：表示编码后平均每个信源符号所能载荷的最大信息量

编码效率：

码的剩余度：

五．哈夫曼编码（重点，简单信源（N次扩展信源）编码，计算)

1.二元huffman编码

最小

2.n元huffman编码：

信源调整q=（r-1）θ+r，θ为信源缩减次数，为正整数。

六．香农编码，费诺编码（重点：编码，特点）

文章来源: blog.csdn.net，作者：渣渣ye，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/yyfloveqcw/article/details/124393041