数字信号处理之期中斩神篇（一重 搬山）
一个视频带你了解傅里叶变换全过程
傅里叶级数视频解析
目录
数字频率与模拟角频率的关系：
为正弦序列的数字域频率(数字频率)，单位是弧度(rad)，表示序列变化的速率，或表示相邻两个序列值之间变化的弧度数。
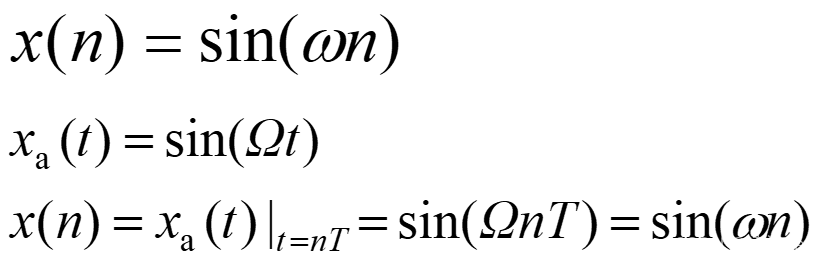
1、凡是由模拟信号采样得到的序列，模拟角频率Ω与序列的数字域频率ω成线性关系。
2、数字域频率是模拟角频率对采样频率的归一化频率。
3、ω表示数字域频率，Ω和f表示模拟角频率和模拟频率。
线性系统：
1.满足叠加原理
2.叠加原理包含可加性和齐次性
时不变系统：
1.系统的响应与输入信号施加于系统的时刻无关
2.运算关系在整个运算过程中不随时间而变化
（直观判断：若出现反转、变系数、展缩即为时变）
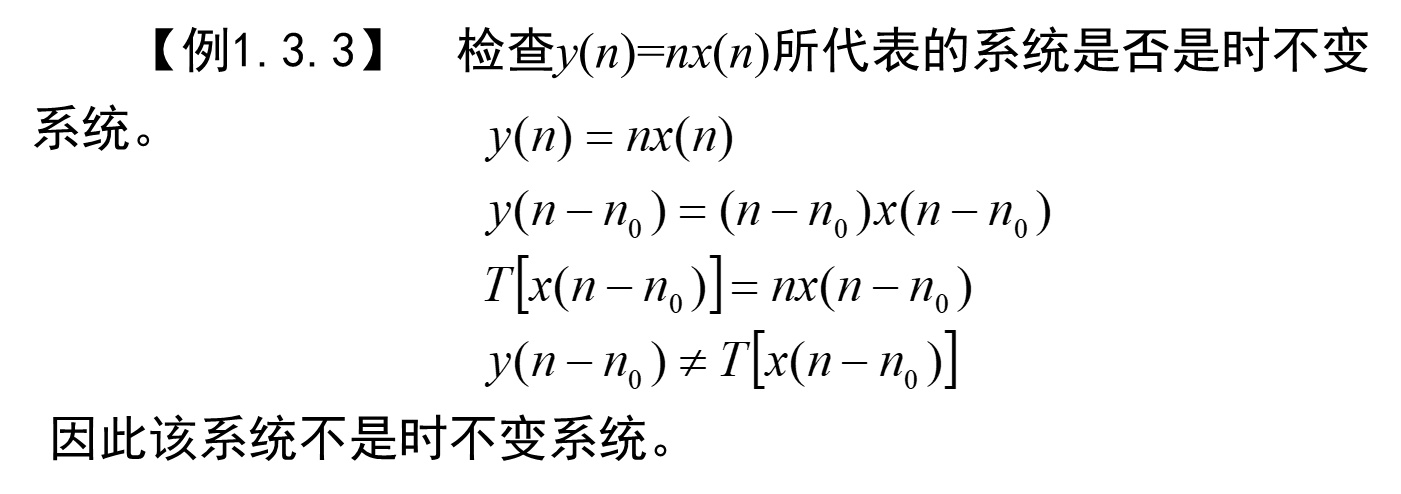
系统的因果性和稳定性：
因果系统：系统某时刻的输出y(n)只取决于此时刻x(n)和以前的输入x(n-1)，x(n-2)，…，而和此时刻以后的输入x(n+1)，x(n+2)，…无关。
先因后果：因果系统的响应不会出现于外加输入之前。
非因果系统：当前的输出还取决于未来的输入，不符合因果关系。
稳定系统：对有界输入，系统输出也是有界的。
系统稳定的充分必要条件是系统的单位脉冲响应绝对可和，用公式表示为
采样定理：
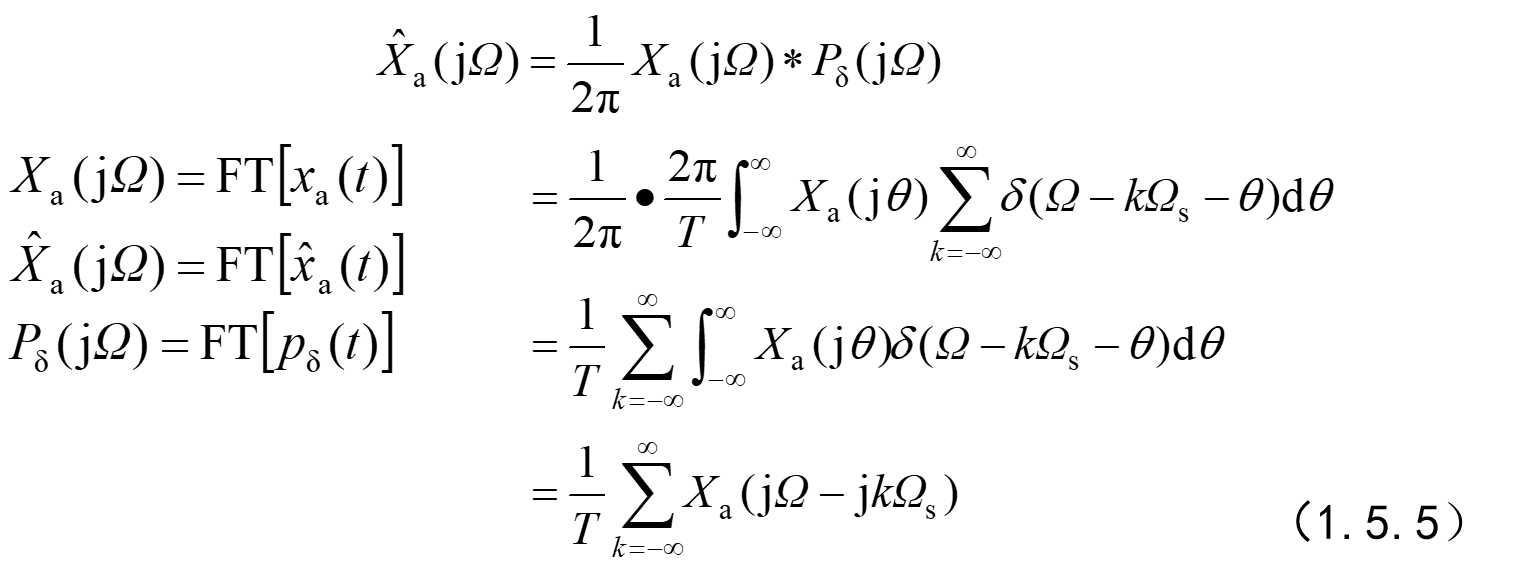
取样信号的频谱是连续时间信号频谱以取样频率为周期进行周期延拓而成
频谱幅度是原信号频谱幅度的1/T倍奈奎斯特取样定理：
要想取样后能够不失真地还原出原信号，则取样频率必须大于两倍信号谱的最高频率。
时域离散信号傅里叶变换：
时移和频移
时域卷积及频域卷积
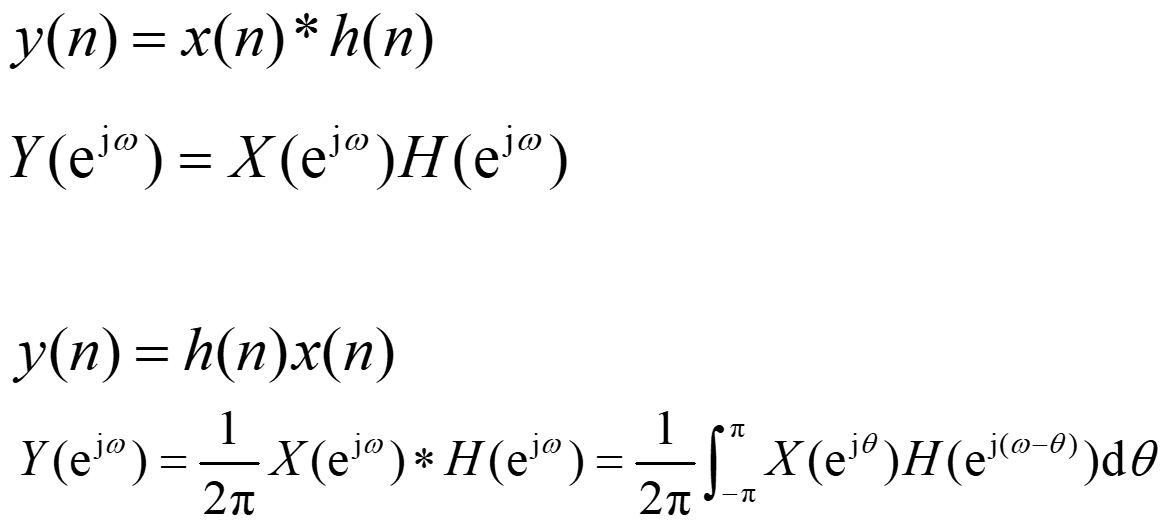
帕斯维尔（Parseval）定理
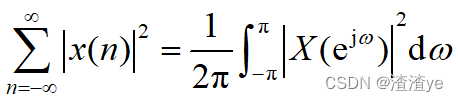
结论：信号时域的能量与频域的能量关系：
1、信号在时域的总能量等于其在频域的总能量；
2、频域的总能量等于能量谱在一个周期内的积分再乘以1/2π 。
序列的反转
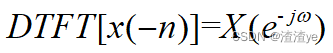
时域反转对应频域反转
序列的共轭
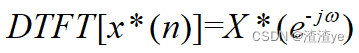
时域共轭对应频域的共轭反转
FT的对称性
一般序列可用共轭对称与共轭反对称序列之和表示：
将上式中的n用－n代替，再取共轭, 得到：
式中，xe(n)和xo(n)可分别用原序列x(n)求出
由上述两式可得：
频域中也有类似性质：
性质：
n序列的DTFT的共轭对称部分，其实部是偶函数，虚部是奇函数。n序列的DTFT的共轭反对称部分，其实部是奇函数，虚部是偶函数。
序列傅里叶变换（DTFT）的共轭对称性
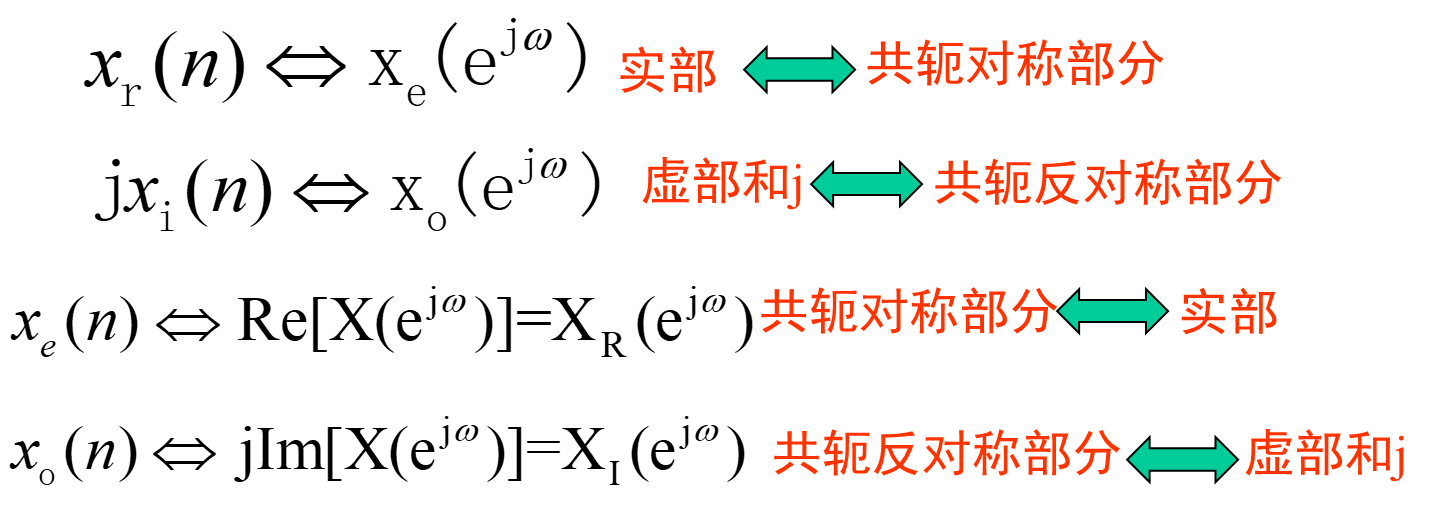
纯实序列：
文章来源: blog.csdn.net，作者：渣渣ye，版权归原作者所有，如需转载，请联系作者。
原文链接：blog.csdn.net/yyfloveqcw/article/details/123933377
- 点赞
- 收藏
- 关注作者
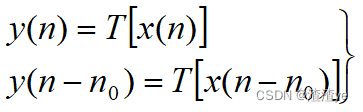
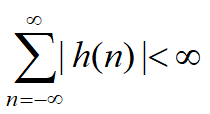
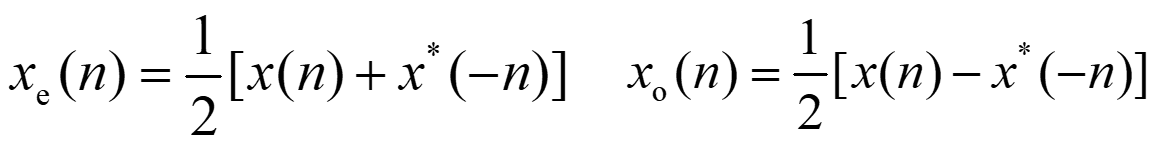
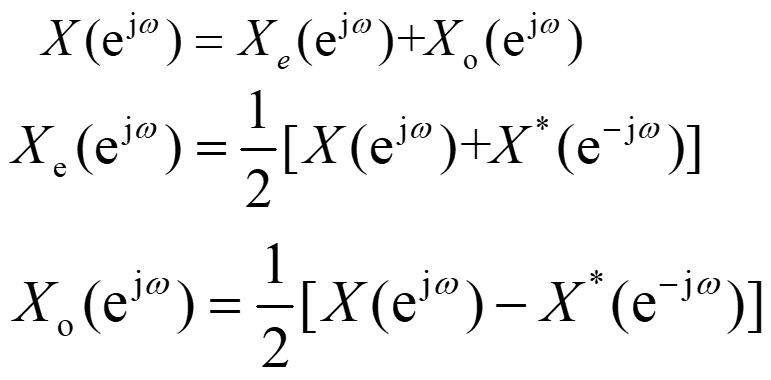
评论（0）