实验三 FFT及其在卷积计算和谱分析中的应用
目录
一、实验目的
1.在理论学习的基础上,通过本实验,加深对FFT的理解,熟悉FFT子程序;
2.熟练掌握FFT实现两个序列的线性卷积的方法;
3.熟悉应用FFT进行信号频谱分析过程中可能出现的问题以便在实际中正确应用FFT;
4. 学习用FFT对连续信号进行谱分析的方法和参数选择原则;
5.掌握用FFT对连续信号进行谱分析时,由模拟信号采样得到序列的
X(k) = DFT[x(n)]中 k 值与模拟信号实际频率 f 或 W 的对应关系。
二、实验内容
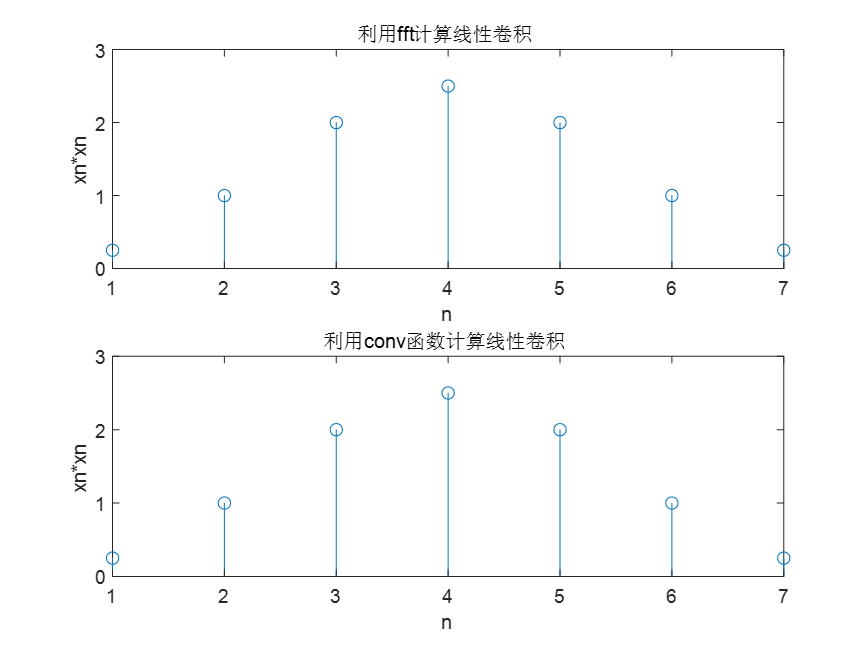
1.已知序列 x(n)=12,1,1,12![]() ,利用FFT计算线性卷积 x(n)*x(n)
,利用FFT计算线性卷积 x(n)*x(n)![]() ,并画出相应的图形。
,并画出相应的图形。
clc,clear,close all
xn=[1/2,1,1,1/2];
Xk=fft(xn,7);
Yk=Xk.*Xk;
yn=ifft(Yk);
subplot(211)
stem(yn)
xlabel('n');
ylabel('xn*xn');
title('利用fft计算线性卷积');
ynn=conv(xn,xn);
subplot(212)
stem(ynn);
xlabel('n');
ylabel('xn*xn');
title('利用conv函数计算线性卷积');
2.对如下模拟周期信号用FFT进行谱分析
x(t)=cos8πt+cos16πt+cos20πt![]()
选择Fs=64Hz,对变换区间 N=16,32,64 三种情况进行谱分析,并回答相应的问题。
- 用stem绘制三种情况下的幅频特性曲线fk~X(k),图中要求显示三种情况的频谱分辨率 F各是多少Hz。
clc,clear,close all
Fs=64;
Ts=1/Fs;
N1=16;
N2=32;
N3=64;
n1=0:1:N1-1;
n2=0:1:N2-1;
n3=0:1:N3-1;
x1=cos(8*pi*n1*Ts)+cos(16*pi*n1*Ts)+cos(20*pi*n1*Ts);
x2=cos(8*pi*n2*Ts)+cos(16*pi*n2*Ts)+cos(20*pi*n2*Ts);
x3=cos(8*pi*n3*Ts)+cos(16*pi*n3*Ts)+cos(20*pi*n3*Ts);
X1=fft(x1,N1);
X2=fft(x2,N2);
X3=fft(x3,N3);
subplot(311)
stem(n1/N1/Ts,abs(X1)/max(abs(X1)));
ylabel("X1 F=4");
xlabel("fk(Hz)");
subplot(312)
stem(n2/N2/Ts,abs(X2)/max(abs(X2)));
ylabel("X2 F=2");
xlabel("fk(Hz)");
subplot(313)
stem(n3/N3/Ts,abs(X3)/max(abs(X3)));
ylabel("X3 F=1");
xlabel("fk(Hz)");
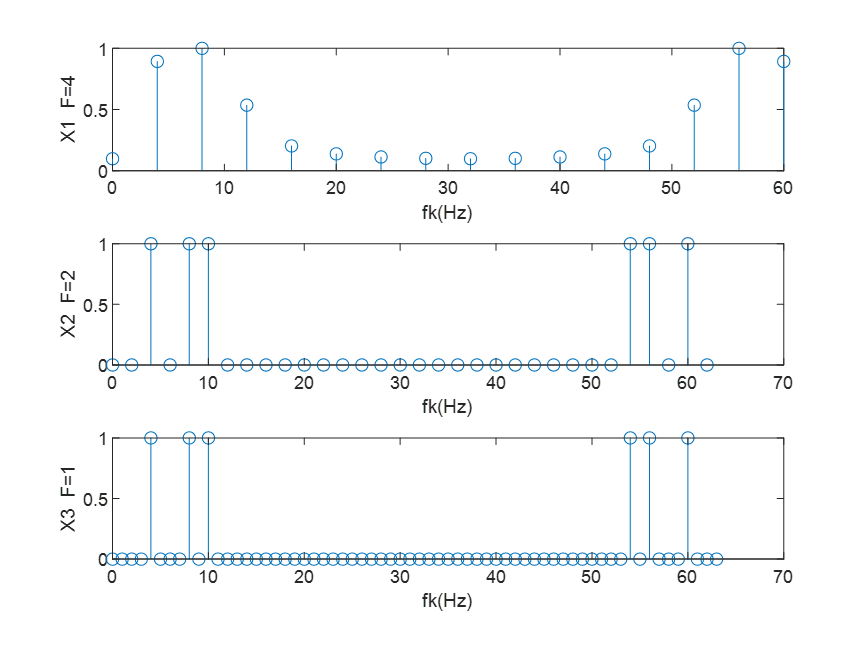
问题 3-1:检查 N=16,32,64 三种情况下谱峰的出现位置,说明哪个是正确的,哪个是不正确的?为什么?
答:N=16不正确,N=32、64是正确的。频率分辨率F=2, Tp应该大于等于1/2,而N=16时,Tp=1/4,所以得到的频谱不正确。
问题 3-2:观察幅频谱图,根据分辨率F读出信号x(n)含有的频率分量分别是多少 Hz?
答:4Hz,8Hz,10Hz,54Hz,56Hz,60Hz。
(2)用plot绘制三种情况的功率谱曲线fk~X(k)。
幅频谱:|X(k)| = abs (Xk)
功率谱:PSD(k)=|X(k)|2/N=X(k)X*(k)/N;
Matlab 语句:PSD = Xk.*conj(Xk)/N;
clc,clear,close all
Ts=1/64;
N1=16;
N2=32;
N3=64;
n1=0:1:N1-1;
n2=0:1:N2-1;
n3=0:1:N3-1;
x1=cos(8*pi*n1*Ts)+cos(16*pi*n1*Ts)+cos(20*pi*n1*Ts);
x2=cos(8*pi*n2*Ts)+cos(16*pi*n2*Ts)+cos(20*pi*n2*Ts);
x3=cos(8*pi*n3*Ts)+cos(16*pi*n3*Ts)+cos(20*pi*n3*Ts);
X1=fft(x1,N1);
X2=fft(x2,N2);
X3=fft(x3,N3);
P1=X1.*conj(X1)/N1;
P2=X2.*conj(X2)/N2;
P3=X3.*conj(X3)/N3;
subplot(311)
plot(n1/N1/Ts,abs(P1));
ylabel("P1(DB) F=4");
xlabel("fk(Hz)");
subplot(312)
plot(n2/N2/Ts,abs(P2));
ylabel("P2(DB) F=2");
xlabel("fk(Hz)");
subplot(313)
plot(n3/N3/Ts,abs(P3));
ylabel("P3(DB) F=1");
xlabel("fk(Hz)");
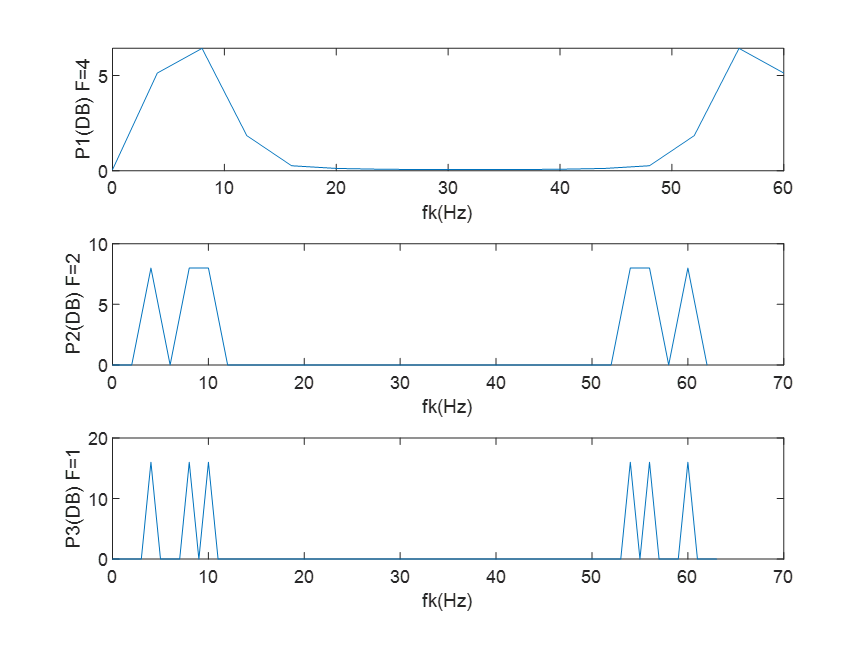
问题 3-3:注意观察频谱的形状和谱峰出现位置,检查有无混叠和泄漏现象?说明产生现象的原因。
答:存在混叠现象。由于不满足奈奎斯特采样定理,在Fs确定条件下,在采样之前未进行预滤波,所以使高于Fs/2的成分折叠而发生混叠。存在泄露现象,由于对原信号进行截断,产生截断效应,使得离散谱线展宽,使其它无频率成分处有了频率成分。
(3)为减少泄露,提高频谱分辨率,另取N值,观察谱分辨率、频谱泄露的改善情况。
clc,clear,close all
Ts=1/64;
N1=128;
N2=512;
N3=2048;
n1=0:1:N1-1;
n2=0:1:N2-1;
n3=0:1:N3-1;
x1=cos(8*pi*n1*Ts)+cos(16*pi*n1*Ts)+cos(20*pi*n1*Ts);
x2=cos(8*pi*n2*Ts)+cos(16*pi*n2*Ts)+cos(20*pi*n2*Ts);
x3=cos(8*pi*n3*Ts)+cos(16*pi*n3*Ts)+cos(20*pi*n3*Ts);
X1=fft(x1,N1);
X2=fft(x2,N2);
X3=fft(x3,N3);
PSD1=X1.*conj(X1)/N1;
PSD2=X2.*conj(X2)/N2;
PSD3=X3.*conj(X3)/N3;
subplot(311)
plot(n1/N1/Ts,abs(PSD1));
ylabel("PSD(DB) F=1");
xlabel("fk(Hz)");
subplot(312)
plot(n2/N2/Ts,abs(PSD2));
ylabel("PSD(DB) F=0.5");
xlabel("fk(Hz)");
subplot(313)
plot(n3/N3/Ts,abs(PSD3));
ylabel("PSD(DB) F=0.25");
xlabel("fk(Hz)");
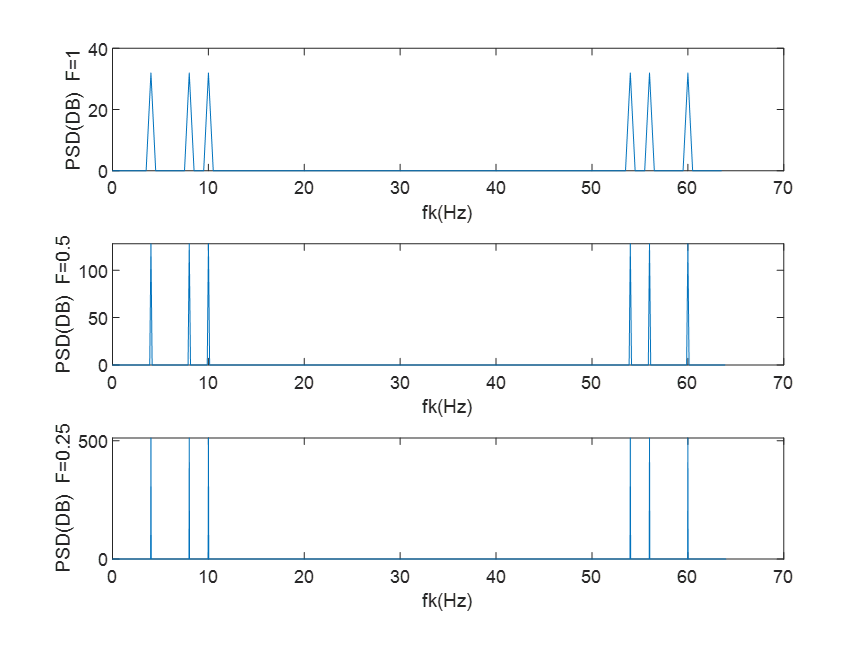
说明,在绘制幅频特性曲线时需注意以下两点:
注意1:
用 DFT(FFT)对模拟信号分析频谱时,需将 X(k)的自变量 k 换算成对应的模拟频率 fk 并作为横坐标绘图,以便于观察频谱。这样,不管变换区间 N 或 Tp取信号周期的几倍,画出的频谱图中有效离散谐波谱线所在的频率值不变。
如图 3-2 所示,
fk=kF=kNTs=kTp,k=0,1⋯N-1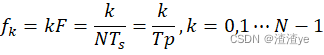
注意2:
对于由截取得到的序列xn,其长度为 N 时,它的DFT 定义为:
X(k)=n=0N-1 x(n)WNkn,WN=e-j2πN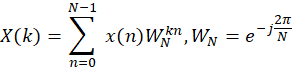
可见随着截取长度导致的 N 值的增大,所计算出来的同一模拟信号的幅频特性幅度值会随着变换区间 N 的变化而变化。为避免幅度值随变换区间 N 变化的缺点,实际上在分析频谱时最好给出对最大值归一化的幅度值。如:stem(fk,abs(Xk)/max(abs(Xk)))。
三、实验思考
1)已知模拟信号x(t)=cos(2πft)![]() ,其中f=50Hz,用DFT(FFT)对此模拟信号分析频谱时,若采样间隔为Ts,采样后的序列x(n)的长度为N, X(k)=DFT[x(n)]
,其中f=50Hz,用DFT(FFT)对此模拟信号分析频谱时,若采样间隔为Ts,采样后的序列x(n)的长度为N, X(k)=DFT[x(n)]![]() ,则k=1对应的连续频率fk为多少?
,则k=1对应的连续频率fk为多少?
用 DFT(FFT)对模拟信号分析频谱时,需将 X(k)的自变量k换算成对应的模拟频率fk并作为横坐标绘图,以便于观察频谱。k=1对应的连续频率fk=1/NTs。
2)对于周期序列,如果周期信号的周期预先不知道,如何使用FFT进行谱分析?
可以先截取预定点数进行DFT,再逐渐将截取长度扩大截取,比较结果,如果二者的差别满足分析误差要求,则可以进行谱分析。
文章来源: blog.csdn.net,作者:渣渣ye,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/yyfloveqcw/article/details/124345110
- 点赞
- 收藏
- 关注作者


评论(0)