- 微信
- 微博
  
  分享文章到微博
- 复制链接
  
  复制链接到剪贴板

2019 第十届蓝桥杯大赛软件赛省赛，C/C++大学B组题解

小哈里发表于 2022/05/10 22:42:53 2022/05/10

【摘要】第1题 —— 组队（5分）考虑到每个人只能选一次，但他可能同时是好几项的最高分，要标记一下选过了不能选。答案490 #include<bits/stdc++.h> using n...

第1题 —— 组队（5分）

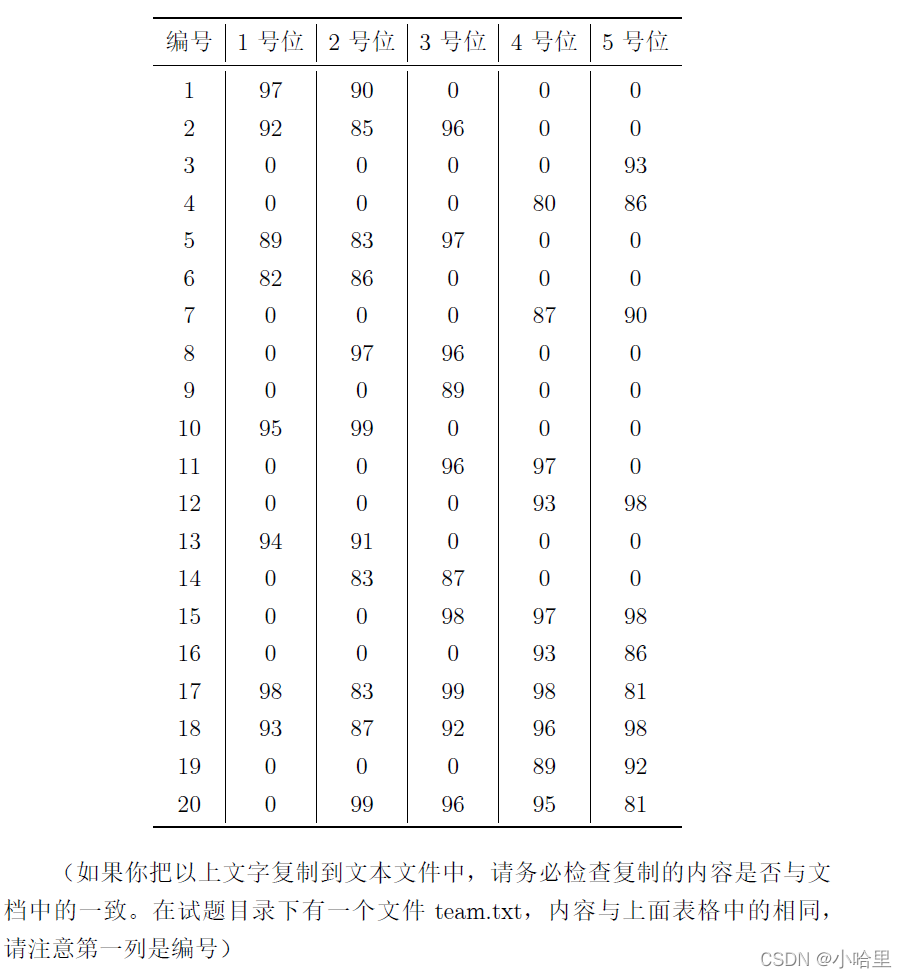
考虑到每个人只能选一次，但他可能同时是好几项的最高分，要标记一下选过了不能选。
答案490

#include<bits/stdc++.h>
using namespace std;

struct node{ int a[7], ok=0; }a[50];

int main(){
    for(int i = 1; i <= 20; i++){
        int x;  cin>>x;
        for(int j = 1; j <= 5; j++){
            cin>>a[i].a[j];
        }
    }
    int res = 0;
    for(int i = 1; i <= 5; i++){
        sort(a+1,a+20+1,[i](node x, node y){
            return x.a[i]>y.a[i];
        });
        for(int j = 1; j <= 20; j++){
            if(a[j].ok==0){
                res += a[j].a[i];
                a[j].ok = 1;
                break;
            }
        }
    }
    cout<<res;
    return 0;
}

第2题 —— 年号字串（5分）

10进制转26进制即可
答案：BYQ

#include<bits/stdc++.h>
using namespace std;

string p = "0ABCDEFGHIJKLMNOPQRSTUVWXYZ";

int main(){
    int n = 2019;
    string t;
    while(n){
        t = p[n%26]+t;
        n /= 26;
    }
    cout<<t;
    return 0;
}

也可以excel拖到2019 hhh

第3题 —— 数列求值（10分）

直接枚举mod10000即可。
答案：4659

#include<bits/stdc++.h>
using namespace std;
const int maxn = 3e8;
int f[maxn];

int main(){
    f[1] = f[2] = f[3] = 1;
    for(int i = 4; i <= 20190324; i++){
        f[i] = (f[i-1]+f[i-2]+f[i-3])%10000;
    }
    cout<<f[20190324];
    return 0;
}

第4题 —— 数的分解（10分）

注意顺序不同算相同，对于x,y,z三个位置相当于有6种摆放位置，我们需要将枚举结果除以6
因为只要分解成三个，可以直接暴力
答案：40785

#include<bits/stdc++.h>
using namespace std;
const int maxn = 3e8;

int check(int x){
    string s = to_string(x);
    if(s.find('2')!=string::npos || s.find('4')!=string::npos)return 0;
    return 1;
}

int main(){
    int res = 0;
    for(int i = 1; i <= 2019; i++){
        for(int j = 1; j <= 2019; j++){
            for(int k = 1; k <= 2019; k++){
                if(i==j || j==k || i==k)continue;
                if(i+j+k==2019 && check(i)&&check(j)&&check(k))res++;
            }
        }
    }
    cout<<res/6<<"\n";
    return 0;
}

第5题 —— 迷宫（15分）

嗯，excel走迷宫可以的，幼儿班益智游戏
不难想到直接bfs，按题目DLRU的顺序转移，对于输出路径可以每个节点记录一下当前的走的路。

01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000

186
DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR

#include<bits/stdc++.h>
using namespace std;

string a[80];

int dir[4][2] = {{1,0},{0,-1},{0,1},{-1,0}};
string dirc = "DLRU";
struct node{int x, y, step; string p;};
int vis[80][80];

int main(){
    int n = 30, m = 50;
    for(int i = 0; i < n; i++)cin>>a[i];
    queue<node>q;
    q.push({0,0,0,""});
    vis[0][0] = 1;
    while(q.size()){
        node t = q.front();  q.pop();
        if(t.x==n-1 && t.y==m-1){
            cout<<t.step<<"\n";
            cout<<t.p<<"\n";
            break;
        }
        for(int i = 0; i < 4; i++){
            int nx = t.x+dir[i][0], ny = t.y+dir[i][1];
            if(nx>=0&&nx<n&&ny>=0&&ny<m){
                // cout<<nx<<" "<<ny<<" "<<a[nx][ny]<<"\n";
                // cout<<vis[nx][ny]<<" "<<a[nx][ny]<<"\n";
                if(!vis[nx][ny] && a[nx][ny]=='0'){
                    q.push({nx,ny,t.step+1, t.p+dirc[i]});
                    vis[nx][ny] = 1;
                }
            }
        }
    }
    return 0;
}

第6题 —— 特别数的和（15分）

n< 10000, 直接暴力枚举判断即可

#include<bits/stdc++.h>
using namespace std;
int check(int x){
    while(x){
        int t = x%10;
        if(t==0 || t==1 || t==2 || t==9)return 1;
        x /= 10;
    }
    return 0;
}

int main(){
    int n;  cin>>n;
    int res = 0;
    for(int i = 1; i <= n; i++){
        if(check(i))res += i;
    }
    cout<<res;
    return 0;
}

第7题 —— 完全二叉树的权值（20分）

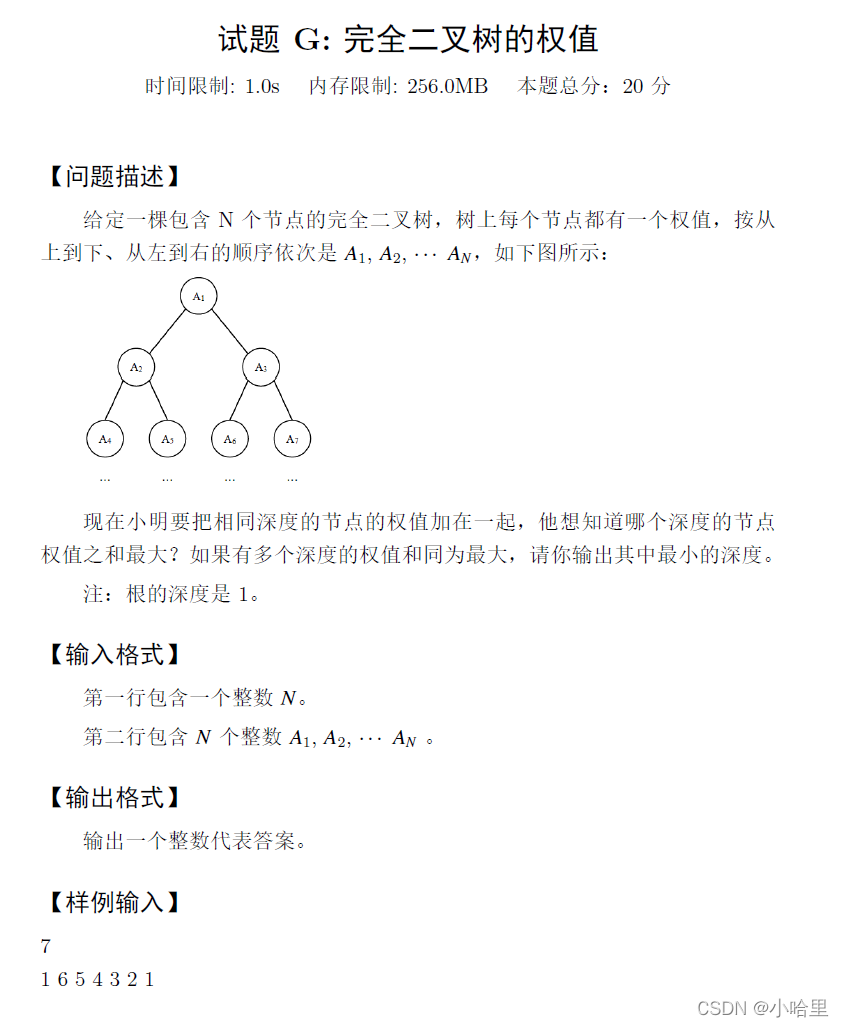
给出一颗二叉树层序遍历每个节点的权值，求哪一层的权值和最大，输出层数
直接1,2，4,8枚举，选个最大即可。
不知道为啥，怎么交都只有80分

//80分
#include<bits/stdc++.h>
using namespace std;

int main(){
    int n;  cin>>n;
    int x = 1, y = 1;
    int c, ans=-1;
    for(int i = 1; i <= n; i += y){
        int t = 0;
        for(int j = i; j < i+y; j++){
            int x;  cin>>x;  t += x;
        }
        if(t > ans){
            ans = t;
            c = x;
        }
        x++;
        y *= 2;
    }
    cout<<c;
    return 0;
}

第8题 —— 等差数列（20分）

包含n个数的最短等差数列，所以首先肯定的是，第一项就是最小的数，数列的末项就是最大的数，中间一定能恰好凑出一个等差数列（假设有比末项更大的一定不会更优）
令每个数都减去a1，即都为xd的形式，所以要求的就是最大公差，即剩余整个数列的最大公约数。
最后可以(an-a1)/d+1就是最短长度。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int a[maxn];

int main(){
    int n;  cin>>n;
    for(int i = 1; i <= n; i++)cin>>a[i];
    sort(a+1,a+n+1);
    for(int i = 2; i <= n; i++)a[i]-=a[1];
    int d = a[2];
    for(int i = 2; i <= n; i++){
        d = __gcd(d, a[i]);
    }
    if(d == 0)cout<<n<<"\n";
    else cout<<a[n]/d+1<<"\n";
    return 0;
}

第9题 —— 后缀表达式（25分）

n个加号，m个减号，n+m+1个整数，一共是2(n+m)+1，所以令数字和符号都为节点，可以建立一棵树。
对于减号，要让值最大，可以考虑2-（-a-b-c-d），2-（-a-b+c）结构，即先用负号把负数都减掉，然后多出来的再减较小的正数。

 //70 分 
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 2e5+10;
int a[maxn];
int main(){
    int n, m;  cin>>n>>m;
    int k = n+m+1;
    LL sum = 0;
    for(int i = 0; i < k; i++){
        cin>>a[i];  sum += a[i];
    }
    sort(a, a+k);
    if(a[0] >= 0){ //全是正数，有负号，减一个就好
        if(m)sum -= 2*a[0];
    }else{ //有负号就把所有的负数减掉,多出来的减较小的正数
        for(int i = 0; i < k && a[i]<0 && m>0 ;i++){
            sum -= a[i]*2;
            m--;
        }
    }
    cout<<sum<<"\n";
    return 0;
}

第10题 —— 灵能传输（25分）

原序列为：a1 a2 a3 a4 … an
原序列的前缀和：s1,s2,s3,s4,…,sn
若选择a2进行灵能传输
序列变为: a1+a2,-a2,a3+a2,a4,…,an:
前缀和变为：s2,s1,s3,s4,…,sn
可以发现1,2的前缀和交换了,
也就是我们可以交换任意前缀和，
来使max[si-s(i-1)]最小（所有相邻两个前缀和差值的最大值）。
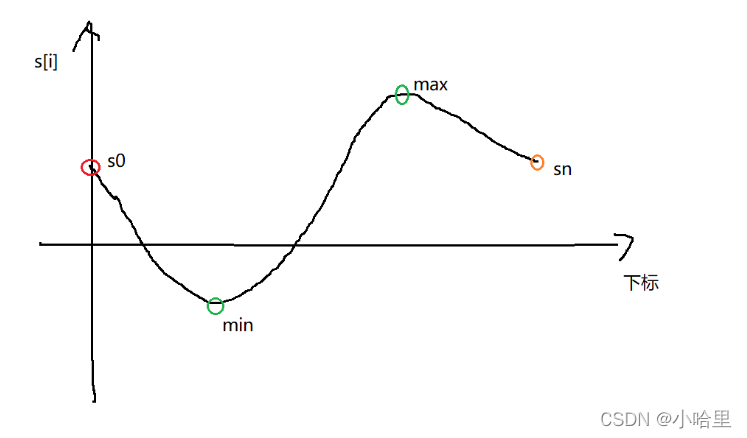
那么我们只要按照大小顺序排列即可求的答案。
这里还有一个问题是，s0 和 sn 不能参与交换。
所以在上述的基础上，考虑s0,sn不参与交换，s0 作为起点，sn作为终点，
然后每次选一个si，作为下一步（也就是新序列重新排列的元素），直到每个si （0<i<n）都选过一次。让整体序列相邻差值最小。
图示方式应该就是最佳路线。

//92分
#include<bits/stdc++.h>
using namespace std;


#define IOS ios::sync_with_stdio(0), cin.tie(0),cout.tie(0)
typedef long long LL;
const LL maxn = 1e5+10;
LL a[maxn], s[maxn], vis[maxn];

int main(){
    IOS;
    int T;  cin>>T;
    while(T--){
        memset(s,0,sizeof(s));
        memset(a,0,sizeof(a));
        memset(vis,0,sizeof(vis));
        int n;  cin>>n;
        for(int i = 1; i <= n; i++){
            cin>>s[i];  s[i] = s[i-1]+s[i];
        }
        LL s0 = s[0], sn = s[n];
        if(s0 > sn)swap(s0, sn);
        sort(s, s+n+1);
        for(int i = 0; i <= n; i++){
            if(s[i] == s0){s0 = i; break; }
        }
        for(int i = n; i >= 0; i--){
            if(s[i] == sn){sn = i; break; }
        }
        //从s0到min, 递减
        int l = 0, r = n;
        for(int i = s0; i >= 0; i-=2){
            a[l++] = s[i];  vis[i] = 1;
        }
        //从max到sn, 递减
        for(int i = sn; i <= n; i+=2){
            a[r--] = s[i];  vis[i] = 1;
        }
        //中间的，递增
        for(int i = 0; i <= n; i++){
            if(vis[i] == 0)a[l++] = s[i];
        }
        //统计答案
        LL res = 0;
        for(int i = 1; i <= n; i++){
            res = max(res, abs(a[i]-a[i-1]));
        }
        cout<<res<<"\n";
    }
    return 0;
}

文章来源: gwj1314.blog.csdn.net，作者：小哈里，版权归原作者所有，如需转载，请联系作者。

原文链接：gwj1314.blog.csdn.net/article/details/124044310

点赞
收藏
关注作者

0/1000

抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认取消

加入云驻计划，成为创作者

华为云周边好礼
免费体验产品
特殊身份标识
线下官方门票
内部专家零距离
与10000+优质创作者共同成长

立即加入

2019 第十届蓝桥杯大赛软件赛省赛，C/C++大学B组题解

第1题 —— 组队（5分）

第2题 —— 年号字串（5分）

第3题 —— 数列求值（10分）

第4题 —— 数的分解（10分）

第5题 —— 迷宫（15分）

第6题 —— 特别数的和（15分）

第7题 —— 完全二叉树的权值（20分）

第8题 —— 等差数列（20分）

第9题 —— 后缀表达式（25分）

第10题 —— 灵能传输（25分）

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

2019 第十届蓝桥杯大赛软件赛省赛，C/C++大学B组题解

第1题 —— 组队 （5分）

第2题 —— 年号字串 （5分）

第3题 —— 数列求值 （10分）

第4题 —— 数的分解 （10分）

第5题 —— 迷宫 （15分）

第6题 —— 特别数的和 （15分）

第7题 —— 完全二叉树的权值 （20分）

第8题 —— 等差数列 （20分）

第9题 —— 后缀表达式 （25分）

第10题 —— 灵能传输 （25分）

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

推荐阅读

相关产品

第1题 —— 组队（5分）

第2题 —— 年号字串（5分）

第3题 —— 数列求值（10分）

第4题 —— 数的分解（10分）

第5题 —— 迷宫（15分）

第6题 —— 特别数的和（15分）

第7题 —— 完全二叉树的权值（20分）

第8题 —— 等差数列（20分）

第9题 —— 后缀表达式（25分）

第10题 —— 灵能传输（25分）