人工神经网络

@TOC
本文所有代码均在 jupyter 环境下编译通过，使用的框架包含 numpy 1.19.5, keras 2.5.0 sklearn 0.24.2 matplotlib 3.4.2

一、神经元

1、感知机

  深度学习模拟人脑神经网络进行分析学习，人脑神经网络由大量神经元构成，神经元接受突触传来的电位信号并整合这些信号，当信号总和达到阈值，神经元将产生兴奋或者抑制。

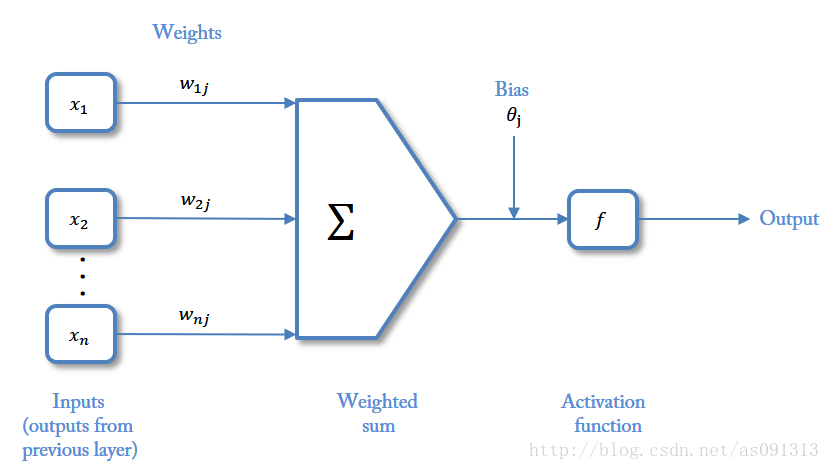
符号表示：

$x_n$ ：输入信号

$w_{ij}$ ：突触权值（为正表示激活，为负表示抑制）

$\Sigma$​ ：一个求和单元，求取各输入信号的加权和（线性组合） $\sum = \sum\limits_i{\omega_iX_i} = \omega^TX$

$\theta_j$ ：神经元固有偏置（阈值）

$f$ ：非线性激活函数，起非线性映射作用并将神经元输出幅度限制在一定范围内（一般在（0， 1）或（-1， 1）之间）

$$u_i = \sum\limits^p_{j=1} {w_{ij}x_j} \\ v_i = u_i - \theta_j \\ y_i = f(v_i)$$

  若把输入的维数增加一维，则可把阈值 $\theta_j$ 包括进去（有没有感觉 $v_i$的公式和最小二乘法一模一样）：

$$v_i = \sum\limits^p_{j=0}w_{ij}x_j \\ y_i = f(v_i)$$

  此处增加了一个新的连接，其输出 $x_0 = \pm 1$，权值 $w_{i0} = \theta_k$​​ ，偏置通过增加一个常数因子从而提供线性模型模拟直线族的能力。

  感知机的参数更新规则通过求解梯度得到，其中 $\eta$ 用于调整感知机的学习率，以确定感知机错误时的学习幅度。参数 $x_i$ 是对应的第 i 个学习样本，而 $\Delta y_i$ 则是对应预测值与真实值的误差，以二分类为例，预测正确时 $\Delta y = 0$，反之为1.

$$\omega \leftarrow \omega + \eta \Delta y_i x_i \\ b \leftarrow b + \eta \Delta y_i$$

2、激活函数

  可参考深度学习中的激活函数[^ 1]

• 饱和激活函数：Sigmoid，Tanh
• 非饱和激活函数：ReLU，Leaky Relu， ELU，PReLU，RReLU

2.1 阈值函数

$$f(v) = \begin{cases} 1, & \text{v $\ge$ 0} \\ 0, & \text{v < 0} \end{cases}\tag{1}$$

即阶梯函数，其中 $v_i = \sum\limits^p_{j=1}w_{ij}x_j - \theta_i$ ，此种神经元为 $M-P$模型。

2.2 分段线性函数

$$f(v) = \begin{cases} 1, & \text{v$\ge$1} \\ \frac{1 + v}{2}, & \text{-1 < v < 1} \\ 0, & \text{v $\le$ -1} \end{cases} \tag{2}$$

  类似于一个放大系数为1的分线性放大器，当工作于线性区时它是一个线性组合其，放大系数趋于无穷大时变成一个阈值单元。

2.3 Sigmoid函数

   $Sigmoid$ 函数具有良好的数学性质 —— 其导数值可以通过原函数求得，因此无需对 Sigmoid 进行显示求导，另一方面，Sigmoid 函数值域为（0，1），因此对于输入X 较大的情况能够压缩输出到合理的范围内，其定义为

$$Sigmoid(X) = \frac{1}{1+e^{-X}}$$

  Sigmoid 函数图像为

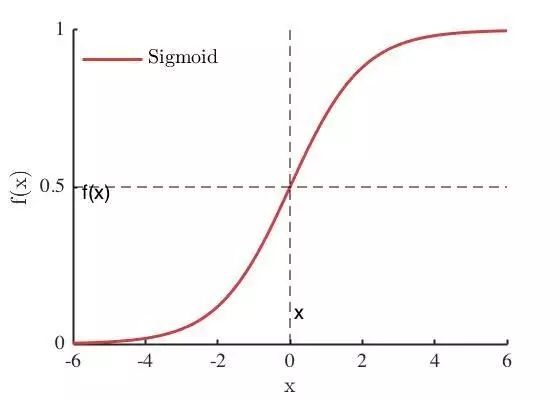
  可见，Sigmoid 在定义域内处处可导，且两侧导数逐渐趋近于0，即： $\lim\limits_{x \to \infty}f'(x) = 0$​ ，这类性质的激活函数被定义为软饱和激活函数。与软饱和相对的是硬饱和激活函数，即： $f'(x) = 0, |x|>c$，c为常数。

  在后向传递过程中，Sigmoid 向下传导的梯度包含了 $f'(x)$因子（ Sigmoid 关于输入的导数），因此一旦落入饱和区， $f'(x) \to 0$​ ，导致向底层传递的梯度也变得非常小，网络参数很难得到有效训练，这种被称之为梯度消失（与之对应的是梯度爆炸），一般 Sigmoid 网络在5层之内就会产生梯度消失现象。

  Sigmoid 的饱和性在物理意义上最接近生物神经元，（0，1）的输出还可以被表示为概率，或用于输入的归一化，代表性的如 Sigmoid 交叉熵损失函数

2.4 Tanh函数

  Tanh 是双曲正切函数，与 Sigmoid 函数相似，Tanh 函数值同样有界，并且函数形状十分类似，同样能将实数域内的值压缩到值域范围内，Tanh 的值域为（-1， 1），Tanh 的函数定义为

$$Tanh(X) = \frac{e^X - e^{-X}}{e^X + e^{-X}} = 2 Sigmoid(2x)-1$$

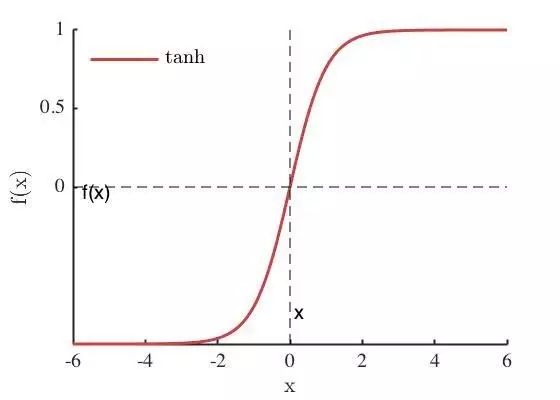
  tanh 也具有软饱和性，因为 tanh 的输出均值比 Sigmoid 更接近0，SGD会更接近 natural gradient，从而降低所需的迭代次数。

2.5 ReLU 函数

  与传统的 Sigmoid 函数相比，ReLU 能有效缓解梯度消失问题，又称为线性修正单元

$$ReLU(X) = max(X, 0) = \begin{cases} X & \text{if $\;$X > 0} \\ 0 & \text{otherwise} \end{cases}$$

  ReLU 在 $x < 0$ 时硬饱和，由于 $x > 0$ 时导数为1， 所以 ReLU能够在 $x > 0$​ 时保持梯度不衰减，从而缓解梯度消失问题，但随着训练推进，部分输入会落入硬饱和区，导致对应权重无法更新，这种现象被称为神经元死亡。

2.6 SoftPlus

  SoftPlus 函数通过高斯变换，在0附近的拐点较为缓和

$$SoftPlus(X) = log(1+e^X)$$

3、梯度下降法[^ 2]

  一个刚刚初始化的神经网络模型中，每个神经元的权重通常是随机初始化的，因此预测的结果往往与数据的真实标签有较大的偏差。

  在最开始的训练过程中，每一轮（epoch）训练的输出中都会存在分类错误的样本，错误的样本为模型的训练提供了依据，神经网络模型会根据错误的信息修正网络中的参数分布情况，从而较好的拟合真实数据集中的特征分布情况这种以输出的误差作为调整信息的信号源，由网络的输出层向网络的输入层逐层传播信息的方法即为反向传播法。

  模型预测值与数的真实标签之间通过损失函数刻画偏差。通过将每个样本的预测误差进行累加，就可以得到最终的总体误差。以均方误差的 $\frac{1}{2}$为例， $loss = \frac{1}{2}\sum\limits_i(y_i - predict_i)^2 \qquad predict_i = F(X_i)$​​

  通过梯度进行迭代试错，减少损失。梯度下降法基于梯度因子，梯度就是沿着函数的各个维度进行求偏导得到的向量。梯度算子描述了函数上升最快的方向，因此，更新参数时，将会沿着梯度的反方向更新参数。

  以 Sigmoid 函数求导为例: S = Sigmoid

$$S(x)' = (\frac{1}{1+e^{-x}})' = \frac{e^{-x}}{(1+e^{-x})^2} \\ =\frac{(1 + e^{-x}) -1}{(1 + e^{-x})^2}\\ = \frac{1}{1+e^{-x}} - \frac{1}{(1 + e^{-x})^2} \\ = \frac{1}{1 + e^{-x}}(1 - \frac{1}{1 + e^{-x}}) \\ = S(x)(1 - S(x))$$

  在高维空间中，沿着各个轴方向分别求解偏导数所组成的向量即为梯度，调整参数的过程即为通过梯度的反方向结合步长，根据模型输出的预测结果与实际值之间的误差进行反馈调整： $\omega \leftarrow \omega - \eta \Delta loss(\omega)$

  对 $loss$ 进行求导，结合 Sigmoid 求导，可得线性单元中损失函数的梯度：

$$\Delta loss (\omega) = \frac{\partial loss(\omega)}{\partial \omega} \\ = \frac{1}{2} \sum\limits_{i} \frac{\partial(y_i -F(x_i))^2}{\partial \omega} \\ = \sum\limits_i (y_i - F(x_i))\frac{\partial(-F(x_i))}{\partial \omega} \\ = - \sum\limits_i (y_i - F(x_i))x_i$$

  得到 $\omega \leftarrow \omega + \eta\sum\limits_i(y_i - F(x_i))x_i$

---

4、感知机的原生实现[^ 2]

  常用的Python深度学习框架包括 Tensorflow, Pytorch, MXnet, Caffe, Keras等， 以下通过 numpy 实现一个简易感知机进行与或非三种基本逻辑运算的代码

import numpy as np

# 激活函数
def activate(X):
    '''
    该激活函数为一个阶跃函数
    Arg: X 输入参数矩阵 X
    Return: X: 激活后的值
    '''
    X[X > 0], X[X < 0] = 1, 0
    return X

# 在参数矩阵中加入偏置项 bias
def add_bias(X):
    '''
    Args: X: 输入参数矩阵X
    '''
    if X.ndim == 1:
        X = X.reshape(len(X), 1)
    return np.hstack([X, np.ones((len(X), 1))])

# 训练感知机
def train(X, Y, eta=0.2):
    '''
    Args: 
    	X: 输入参数矩阵
    	Y: 指定标签列表
    	eta: 学习率，默认值设为0.2
    	
    Return:
    	omega: 权重向量与偏置项
    '''
    # 初始化权重向量，其中包含偏置项的权重
    omega = np.zeros(X.shape[1])
    # 开始权重训练过程
    while True:
        # 计算样本预测与标签的误差
        delta = Y - predict(omega, X)
        if (abs(delta) > 0).any():
            # 更新权重及偏置
            omega += eta * np.sum((delta * X.T).T, axis=0)
        else :
            return omega
        
# 根据输入参数预测结果
def predict(omega, X):
    '''
    Args:
    	omega: 权重与偏置构成的矩阵
    	X: 输入参数矩阵
    Return:
    	res: 预测结果
    '''
    return activate(omega.dot(X.T))

# 将传入的数据进行训练， 并将数据打乱后进行测试
def train_and_evaluate(X, Y, X_test, Y_test, eta=0.1):
    '''
    Args:
    	X: 输入参数矩阵
    	eta: 学习率
    '''
    # 加入偏置项bias
    X_bias = add_bias(X)
    # 执行训练并返回参数
    omega = train(X_bias, Y, eta=eta)
    # 输出训练参数
    info = ''.join(['权重 %d: %.4f\n' % (i+1, w) for i, w in enumerate(omega[:-1])])
    info += + '偏置项: %.4f\n' % omega[-1]
    print(info)
    # 评估训练结果
    X_test_bias = add_bias(X_test)
    Y_pred = predict(omega, X_test_bias)
    # 输出测试标签与预测结果
    print('True: Y = %s', Y_test)
    print('Predict: Y = %s', Y_pred)
   
# 构造数据训练集与测试集
def prepare_data(data_type = 'and'):
    '''
    Args:
    	type: 构造的数据集类型，与或非
    '''
    data_type = data_type.lower()
    if data_type in ['and', 'or']:
        X = np.asarray([[1, 1],
                       [1, 0],
                       [0, 1],
                       [0, 0]])
        Y = np.asarray([1, 0, 0, 0] if data_type == 'and' else [1, 1, 1, 0])
    elif data_type == 'not':
        X = np.asarray([0, 1])
        Y = np.asarray([1, 0])
        
    # 随机打乱输入矩阵 X 和标签 Y
    idx = np.arange(len(X))
    np.random.shuffle(idx)
    X_test = X[idx]
    Y_test = Y[idx]
    return X, Y, X_test, Y_test

---

二、网络结构[^ 3]

  一个生物神经细胞的功能比较简单，而人工神经元只是生物神经细胞的理想化和简单实现，功能更加简单，要想模拟人的脑力，需要很多神经元一起协作来完成复杂的功能。这样通过一定的连接方式或信息传递方式进行协作的神经元可以看成一个网络，就是神经网络。
神经网络的核心组件是层，它是一种数据处理模块，可以将它看出数据过滤器（进去一些数据，出来更有用的数据），大多数深度学习都是将简单的层链接起来，从而实现渐进式 数据蒸馏。

1、前馈网络

  前馈网络中各个神经元按接收信息的先后分为不同的组，每一组可以看成一个神经层，每一层的神经元接收前一层神经元的输出，并输出到下一层神经元。整个网络的信息是朝一个方向传播，没有反向传播的信息。

  前馈网络可以看成是一个函数，通过简单非线性函数的多次复合，实现输入空间到输出空间的复杂映射。

2、记忆网络

  也称为反馈网络，网络中的神经元不但可以接收其他神经元的信息，也可以接收自己的历史信息，和前馈网络相比，记忆网络中的神经元具有记忆功能，在不同时刻有不同的状态。

3、图网络

  图网络是定义在图结构数据上的神经网络，图中每个节点都由一个或一组神经元构成，节点之间的连接可以是有向的，也可以是无向的，每个节点可以收到来自相邻节点或自身的信息。

---

三、前馈网络和反向传播算法

  推荐一组视频：三蓝一棕深度学习系列，讲的比较易懂透彻。

  也被称为多层感知器，由多层 Logistic 回归模型组成，在这个网络中，每一层的神经元可以接收前一层的神经元的信号，并产生信号输出到下一层，，第0层被称为 输入层，最后一层被称为 输出层，其他中间层称为 隐藏层。整个网络中无反馈，信号从输入层向输出层单向传播。

$L$：神经网络层数

$M_l$ ：第 $l$ 层神经元的个数

$f_l(\cdot)$：第 $l$​ 层神经元的激活函数

$W^{(l)} \in R^{M_l \times M_{l-1}} $：第 $l - 1$ 层到第 $l$​ 层的权重矩阵

$b^{(l)} \in R^{M_l}$：第 $l-1$ 层到第 $l$ 层的偏置

$z^{(l)} \in R^{M_l}$：第 $l$ 层神经元的净输入（净活性值）

$a^{(l)} \in R^{M_l}$：第 $l$ 层神经元的输出（活性值）

  令 $a^{(0)} = x$，前馈神经网络通过不断迭代下面公式进行信息传播：

$$z^{(l)} = W^{(l)}a^{(l-1)}+b^{(l)} \\ a^{(l)} = f_l(z^{(l)}) \tag{1}$$

  第 $l-1$ 层神经元的活性值 $a^{l-1}$ 计算出第 $l$ 层神经元的净活性值 $z^{(l)}$​，然后经过一个激活函数得到第 $l$ 层神经元的活性值，因此，可以把每个神经层看作一个 仿射变换 和一个非线性变化。

$$z^{(l)} = W^{(l)} f_{(l-1)} (z^{(l-1)}) + b^{(l)} \\ 或者 \qquad a^{(l)} = f_l(W^{(l)} a^{(l-1)} + b^{(l)})$$

  要想控制一个事物，首先要能够观察它，因此神经网络损失函数的任务就是衡量输出与预测之间的距离，接着利用这个距离值作为反馈信号来对权重进行微调，以降低损失函数的值，这种调节由优化器完成，它实现了 反向传播算法，也就是常说的 BP神经网络：
BP神经网络是一种多层的前馈神经网络，其主要的特点是：信号是前向传播的，而误差是反向传播的。
  BP神经网络的过程主要分为两个阶段，第一阶段是信号的前向传播，从输入层经过隐含层，最后到达输出层；第二阶段是误差的反向传播，从输出层到隐含层，最后到输入层，依次调节隐含层到输出层的权重和偏置，输入层到隐含层的权重和偏置。
以下用代码实现了 BP神经网络 的简单分类与回归。

---

1、代码实现

  利用 python 的上层 API 快速构建神经网络，以手写数字集分类以及sklearn创建的回归数据集为例，由于刚刚接触，代码的实现可能较为笨拙：

1.1 回归

from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_splits

# 创建一个回归数据集，样本数为10000，特征数量为10，回归目标数量为1，噪声值为0.1
(X, y, coef) = make_regression(n_samples=10000, n_features=10, n_targets=1, bias=0.1, noise=0.1, coef=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

from keras.layers import Dense
from keras.models import Sequential

# 创建一个序贯模型（多个网络层的线性堆叠）
model = Sequential()
# 加入隐藏层，神经元数量为10，输入特征量为10维，使用 tanh 函数作为激活函数
model.add(Dense(10, input_dim=10, activation='tanh'))
# 由于回归预测值是单个值，所以输出层神经元数量为1
model.add(Dense(1))
# 打印模型信息
model.summary()

# 打印的模型信息

Model: "sequential_3"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_7 (Dense)              (None, 10)                110       
_________________________________________________________________
dense_8 (Dense)              (None, 1)                 11        
=================================================================
Total params: 121
Trainable params: 121
Non-trainable params: 0
_________________________________________________________________

# 编译模型，优化器为随机梯度下降，损失函数为mse
model.compile(optimizer='sgd', loss='mse')
# 训练模型，模型迭代1000次，每次梯度更新的样本数为64，fit方法会返回一个History对象
his = model.fit(X_train, y_train, epochs=1000, verbose=0, batch_size=64)
# 测试模型，返回误差值和评估标准值，cost 在此是 mse 值
cost = model.evaluate(X_test, y_test, batch_size=500)

  接下来看一看损失函数的图像

  可以看到几乎在训练开始损失函数的值就降到了最低，如果想提前终止训练，可以调用 keras.callbacks 内的函数并作为 fit 方法 callbacks 属性的参数。

看一下回归效果 R2 的评分

from sklearn.metrics import r2_score

print(r2_score(y_test, model.predict(X_test)))

0.9855140848830662

  此时模型分数已经接近1了，拟合效果较好，但可能存在过拟合问题。

1.2 分类

from keras.models import Sequential  
from keras.layers.core import Dense, Dropout, Activation  
from keras.optimizers import SGD  
from keras.datasets import mnist  
import numpy 

model = Sequential()
# 以最经典的手写数字识别为例，每张图像尺寸为 28 * 28，因此输入维度为 784
# 创建有两个 500 个神经元的隐藏层，每个神经元会学习到一点特征，学习到什么不需要我们考虑，以 sigmoid 为激活函数
# 为了防止过拟合，每次让一半的神经元停止工作
model.add(Dense(500,input_shape=(784,))) 
model.add(Activation('sigmoid'))  
model.add(Dropout(0.5)) 
model.add(Dense(500))  
model.add(Activation('sigmoid'))  
model.add(Dropout(0.5))
# 手写数字集的数字集为 0-9，共十类，因此用多分类 sotfmax 作为激活函数，输出层设置10个神经元，活性值最高的神经元即是预测结果
model.add(Dense(10)) 
model.add(Activation('softmax')) 
# 梯度下降作为优化器，学习率为0.01
sgd = SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
model.compile(loss='categorical_crossentropy', optimizer=sgd) 
# 载入手写数字集
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(X_train.shape[0], X_train.shape[1] * X_train.shape[2]) 
X_test = X_test.reshape(X_test.shape[0], X_test.shape[1] * X_test.shape[2])  
Y_train = (numpy.arange(10) == y_train[:, None]).astype(int) 
Y_test = (numpy.arange(10) == y_test[:, None]).astype(int)
# 开始训练，训练200次，以训练集的30%作为验证集
model.fit(X_train,Y_train,batch_size=200,epochs=50,shuffle=True,verbose=0,validation_split=0.3)
scores = model.evaluate(X_test,Y_test,batch_size=200,verbose=0
                        
print(scores)
result = model.predict(X_test,batch_size=200,verbose=0)

result_max = numpy.argmax(result, axis = 1)
test_max = numpy.argmax(Y_test, axis = 1)

result_bool = numpy.equal(result_max, test_max)
true_num = numpy.sum(result_bool)
print("")
print(true_num/len(result_bool))

0.148803
0.955900

识别准确率达到了 95.59%

---

四、参考文献

[^ 1]: 深度学习大讲堂 李扬 ，深度学习中的激活函数导引.https://mp.weixin.qq.com/s?__biz=MzI1NTE4NTUwOQ==&mid=2650325236&idx=1&sn=7bd8510d59ddc14e5d4036f2acaeaf8d&mpshare=1&scene=1&srcid=1214qIBJrRhevScKXQQuqas4&pass_ticket=w2yCF/3Z2KTqyWW/UwkvnidRV3HF9ym5iEfJ+Z1dMObpcYUW3hQymA4BpY9W3gn4#rd , 2016-08-01

[^ 2]: 鲁睿元 祝继华，《Keras深度学习》[M]，北京市海淀区玉渊潭南路1号D座；中国水利水电出版社，2019年
[^ 3]: 邱锡鹏，《神经网络与深度学习》[M]，北京市西城区百万庄大街22号；机械工业出版社，2020年