前言

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研。
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 

知其然 知其所以然！

 
本文仅记录自己感兴趣的内容

2.3. 线性代数

2.3.7. 点积（Dot Product）

torch.dot(x, y)

x = torch.arange(4, dtype=torch.float32)
y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)

  

 

  
1
  
2
  
3
 

2.3.8. 矩阵-向量积

torch.mv(A, x)

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
x = torch.arange(4, dtype=torch.float32)
A.shape, x.shape, torch.mv(A, x)

  

 

  
1
  
2
  
3
 

2.3.9. 矩阵-矩阵乘法

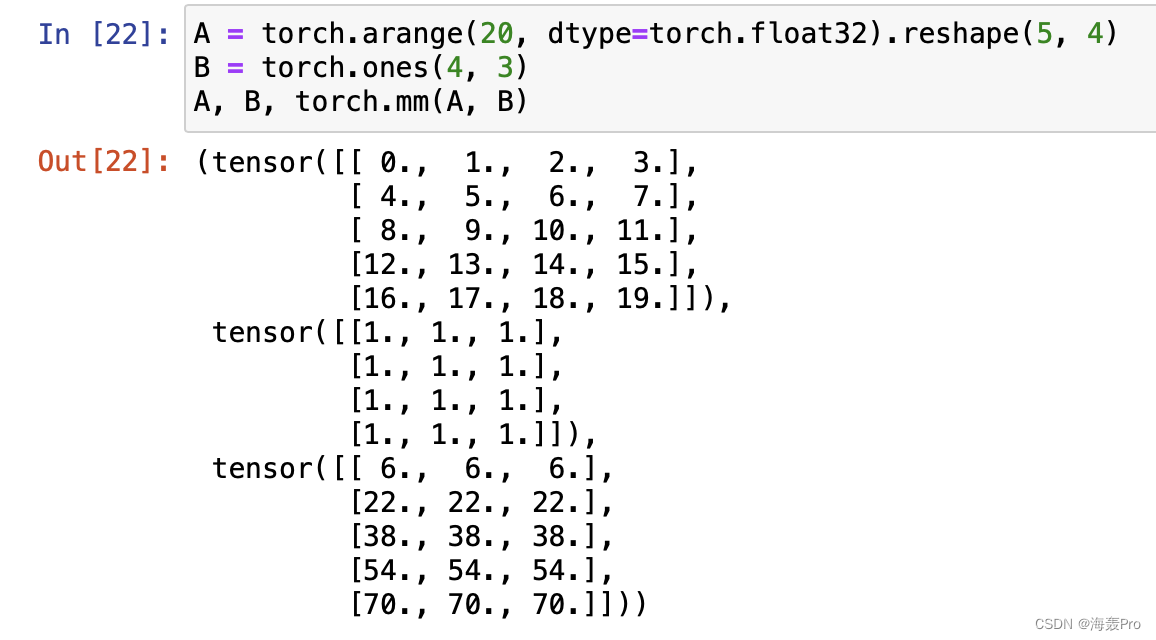
torch.mm(A, B)

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = torch.ones(4, 3)
A, B, torch.mm(A, B)

  

 

  
1
  
2
  
3
 

2.3.10. 范数

非正式地说，一个向量的范数告诉我们一个向量有多大。 这里考虑的大小（size）概念不涉及维度，而是分量的大小。

在线性代数中，向量范数是将向量映射到标量的函数f。

u = torch.tensor([3.0, -4.0])
torch.norm(u)

  

 

  
1
  
2
 

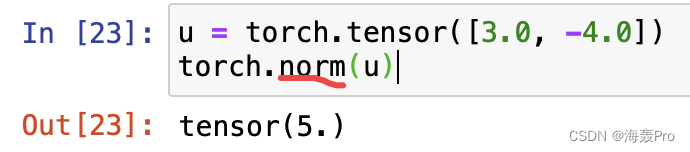
torch.norm()

结语

学习资料：http://zh.d2l.ai/

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正

文章来源: haihong.blog.csdn.net，作者：海轰Pro，版权归原作者所有，如需转载，请联系作者。

原文链接：haihong.blog.csdn.net/article/details/124531994