前言

公钥密码包含两个密钥，加密密钥和解密密钥，其加密密钥是可以公开的，解密密钥是不能公开的。公钥密码自1976年提出这个思想后就不断发展，其一般是基于数学上的一些困难问题所建造的，如rsa基于大整数分解的困难问题建立的，椭圆曲线是基于椭圆曲线上的离散对数困难问题建立的，elgamal上的DH密钥交换是基于有限域的离散对数困难问题建立的，格密码是基于格中困难问题的难解程度建立的等等。但是随着科技的发展，在一定条件下，有些困难问题变得不在困难，如rsa密码体系参数的选取，选取的bit长度随着计算机的发展变得越来越长，这提高了存储空间和计算时间，所以研究新型的公钥体系变得越来越火热。下面将会介绍RSA的基本原理和由于参数选取不当造成的攻击手段。

一、RSA算法

RSA属于非对称加密算法，因为RSA使用了两个不同的密钥分别用于加密和解密，这两个密钥称之为公私钥对，其中公钥用于加密，且公钥是公开的，而私钥用于解密，私钥是私有的。

RSA的计算过程如下：

1. 找到两个大素数p和q，计算出n = pq；

2. 计算出φ(n) = (p-1)*(q-1)，选择一个e，满足1 < e <φ(n)，且gcd(φ(n), e) = 1；

3. 计算出d，使得d满足ed % φ(n) = 1；

此时，已经生成了公私钥对，其中(e, n)为公钥，(d, n)为私钥。

4. 对于明文M，有密文C = M^e % n，此为加密过程；

5. 对于密文C，有明文M = C^d % n，此为解密过程；

二、题目

给定RSA密文[971,922,605,1446,1704,889,2090,605,1899,1915,2088,1988,1235,1032,65,922,958,1988,2144,591,1988,2270,2088,1032,65,958,2233]，已知RSA的公钥为{7,2449}，请还原出对应的明文。
解题脚本如下：

#!/usr/bin/env python
# -*- coding:utf-8 -*-
import math

def isPrime(n):
    if n <= 1:
        return False
    for i in xrange(2, int(math.sqrt(n) + 1)):
        if n % i == 0:
            return False
    return True

def crack(n):
    for p in xrange(2, n):
        for q in xrange(p+1, n):
            if p*q == n and isPrime(p) and isPrime(q):
                return (p, q)

def extGcd(a, b):
    if a < b:
        return extGcd(b, a)
    if b == 0:
        return a, 1, 0
    gcd, x, y = extGcd(b, a%b)
    return gcd, y, x-a/b*y

def getD(n, e):
    p, q = crack(n)
    fai = (p-1)*(q-1)
    gcd, x, y = extGcd(fai, e)
    while y < 0:
        y += fai
    return y

def decrypt(n, e, ciphertext):
    plaintext = []
    d = getD(n, e)
    for num in ciphertext:
        num = pow(num, d, n)
        plaintext.append(chr(num))
    return "".join(plaintext)

if __name__ == "__main__":
    n = 2449
    e = 7
    ciphertext = [971,922,605,1446,1704,889,2090,605,1899,
                  1915,2088,1988,1235,1032,65,922,958,1988,
                  2144,591,1988,2270,2088,1032,65,958,2233]
    plaintext = decrypt(n, e, ciphertext)
    print plaintext

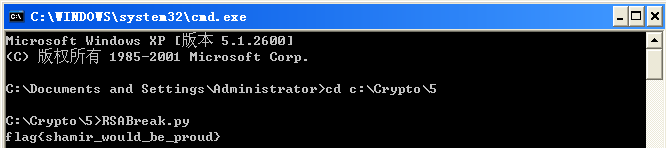
flag为flag{shamir_would_be_proud}