IIR数字滤波器设计及在FDM复用信号滤波中的应用

1.利用双线性变换法，设计Butterworth低通数字滤波器，假设信号，，其中f1=5Hz，f2=30Hz。要求通带波纹小于1dB，幅度衰减大于15dB，采样周期 T=0.01s。

用间接设计方法设计数字低通 DF 的步骤：

(1)产生时域信号xt

要求给出xt的时域波形图。

(2)信号xt的频谱分析

确定采样频率和采样点数N=64; Fs=64;对xt信号进行采样得到序列xtnT。要求给出 xt的频谱图。

k=0:N-1;

wk=2*pi/N*k;  % k对应的数字频率

stem(wk/pi,abs(Xk)/max(abs(Xk)));  %为避免幅度值随变换区间N变化的缺点，画图时可归一化幅度谱。

提示：通带截止频率大致为Ωp=0.2Π，通带截止频率大致为Ωs=0.3Π

(3)根据读出的数字滤波器的截止频率及已知的通带波纹、阻带衰减，利用双线性变换法的频率转换形式得到模拟滤波器的频率。

(4)IIR 数字滤波器的设计及实现

①本实验采用 Butterworth 模拟滤波器设计来完成相应低通滤波器的设计，具体可调用 buttord、butter 函数完成 DF 设计。

②滤波实现

可调用滤波器实现函数 filter 来完成此功能。

要求1：绘图显示低通滤波器的损耗函数曲线；

要求2：显示滤波后的时域波形图，观察滤波效果。

clc,clear,close all
% 数字低通技术指标
wp=0.2*pi;
ws=0.3*pi;
ap=1;
as=15;
T=0.01;

% 产生时域信号xt，要求给出xt的时域波形图
f1=5; f2=30;
t=0:0.001:1;
xt=sin(2*pi*f1*t)+0.5*cos(2*pi*f2*t);
subplot(221)
plot(t,xt)
xlabel('t');
ylabel('xt');
title('时域信号xt')
grid on

% xt的频谱分析 
N=64;
Fs=64;
Ts=1/Fs;
k=0:N-1;
xnT=sin(2*pi*f1*k*Ts)+0.5*cos(2*pi*f2*k*Ts);
Xk=fft(xnT,N);
wk=2*pi/N*k;% k对应的数字频率
subplot(222)
stem(wk/pi,abs(Xk)/max(abs(Xk)));   %为避免幅度值随变换区间N变化的缺点，画图时可归一化幅度谱。 
xlabel('w/\pi');
ylabel('xnT');
title('Xk')
grid on

% 利用双线性变换法的频率转换形式得到模拟滤波器的频率
Wp=(2/Ts)*tan(wp/2);
Ws=(2/Ts)*tan(ws/2);

% IIR 数字滤波器的设计及实现
[NN,Wc]=buttord(Wp,Ws,ap,as,'s');  %之前用过N，这里使用NN表示阶数  
[B,A]=butter(NN,Wc,'s');
[Bz,Az]=bilinear(B,A,Fs);
[H,w]=freqz(Bz,Az,N);
subplot(223);
plot(w/pi,20*log10(abs(H)/max(abs(H))))
xlabel('w/\pi');
ylabel('dB');
title('损耗函数')
grid on

% 滤波后的时域波形图
subplot(224);
yt=filter(Bz,Az,xnT);
plot(k*Ts,yt)
title('滤波后信号的时域波形')
xlabel('t');
ylabel('yt');
grid on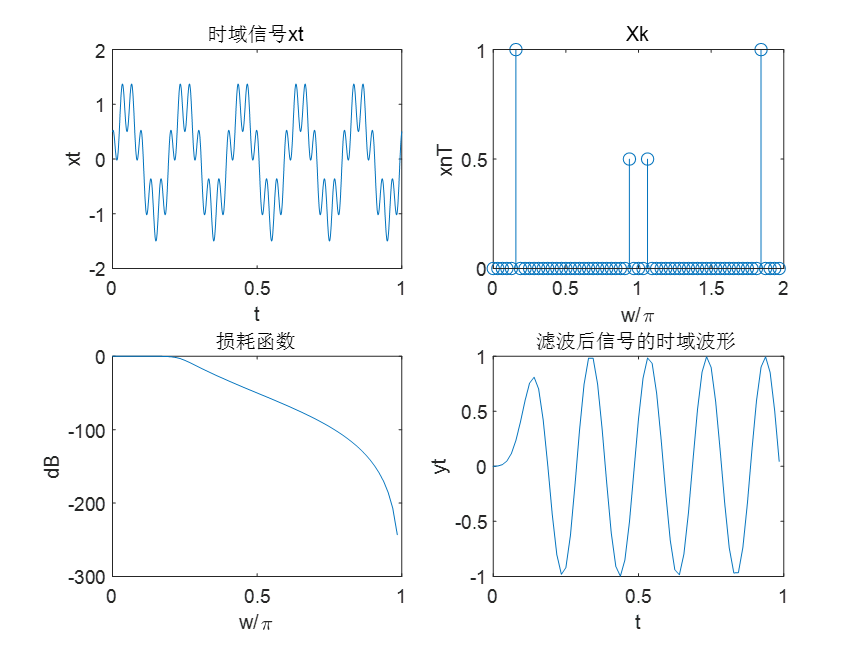

问题1-1：观察xt的频谱图，给出信号xt的频率分量对应的数字频率。

答：0.156Π和0.937Π

问题1-2：给出数字边界频率的双线性转换关系。

答：关系式：Ω=2/T（tanw/2）

2.IIR 滤波器设计在 FDM 频分多路复用信号滤波分离过程中的应用

用数字频率直接设计数字低通 DF 的步骤：

(1)产生三路调幅信号构成的FDM时域复用信号st

已知调制信号形式为fm=cos（2Πft），试分别用频率为30Hz、60Hz、120Hz的三路信号去调制频率为300Hz、600Hz、1200Hz的余弦载波信号，实现三路抑制载波调幅信号，并由三路调幅信号构成FDM复用信号st。

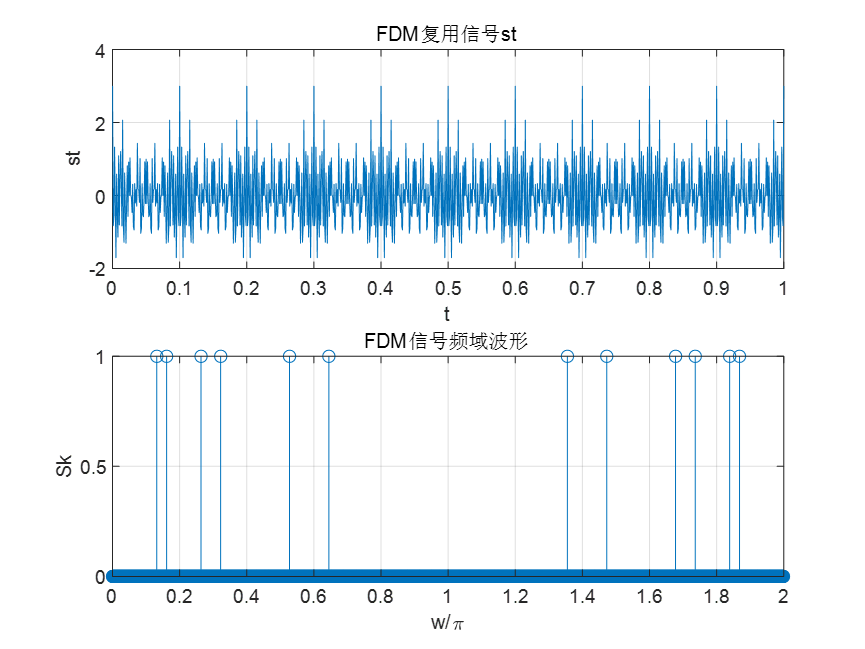
要求给出st的时域波形图。

(2)FDM复用信号st的频谱分析

要求给出st幅频特性曲线。

取N=2048; Fs=4096;对st信号进行采样得到序列stnT。

问题1：观察st的频谱图，分别给出三路调幅信号的数字频率范围。

(3)确定数字滤波器设计指标

根据题目2中读出的三路调幅信号的频率范围，分别确定可以分离 st 中三路调幅信号的三个滤波器（低通、带通、高通）的通带截止频率和阻带截止频率，并要求滤波器的通带最大衰减为 0.1dB，阻带最小衰减为 60dB。

说明：为了使滤波器阶数尽可能低，每个滤波器边界频率的选择原则是尽量使滤波器过渡带宽一些。

 (4)IIR 数字滤波器的设计及实现

①本实验选用椭圆滤波器完成相应滤波器的设计，具体可利用数字频率指标调用ellipord 和ellip函数完成DF设计。

②滤波实现

用三个滤波器分别对信号st进行滤波，分离出st中的三路不同载波频率的调幅信号 y1(n)、y2(n)、y3(n)。可调用滤波器实现函数filter来完成此功能。

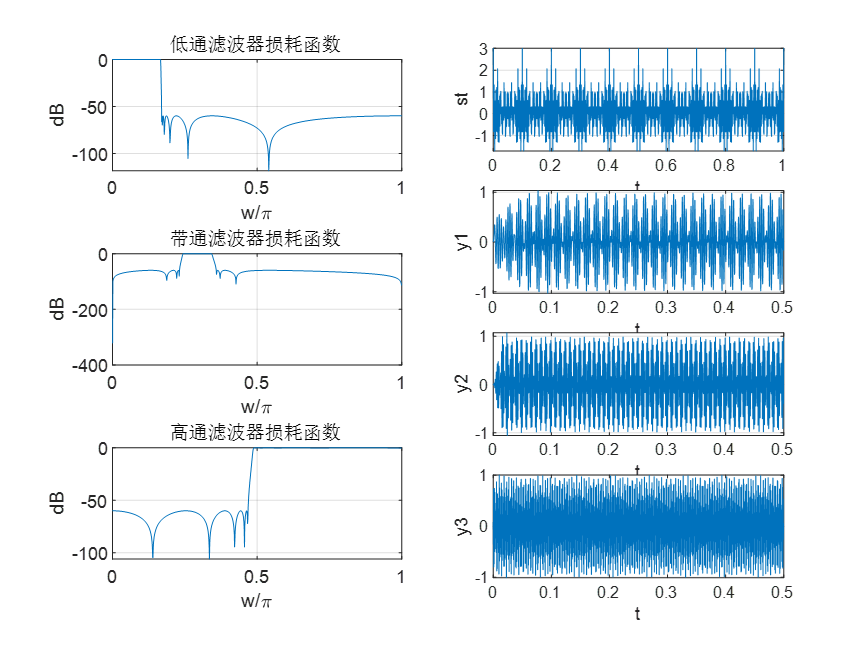
要求1：绘图显示各滤波器的损耗函数曲线；

要求2：显示 y1(n)、y2(n)和 y3(n)的时域波形图，观察分离效果。

时频域信号分析：

clc,clear,close all

% 产生三路调幅信号构成的FDM时域复用信号st
t=0:0.001:1;
fm1=cos(2*pi*30*t);
fm2=cos(2*pi*60*t);
fm3=cos(2*pi*120*t);
f1=cos(2*pi*300*t);
f2=cos(2*pi*600*t);
f3=cos(2*pi*1200*t);
st=fm1.*f1+fm2.*f2+fm3.*f3;
subplot(211)
plot(t,st);
xlabel('t');
ylabel('st');
title('FDM复用信号st')
grid on

% FDM复用信号st的频谱分析
N=2048;
n=0:N-1;
Fs=4096;
Ts=1/Fs;
fm11=cos(2*pi*30*n*Ts);
fm22=cos(2*pi*60*n*Ts);
fm33=cos(2*pi*120*n*Ts);
f11=cos(2*pi*300*n*Ts);
f22=cos(2*pi*600*n*Ts);
f33=cos(2*pi*1200*n*Ts);
stnT=fm11.*f11+fm22.*f22+fm33.*f33;
Sk=fft(stnT,N);
wk=2*pi/N*n;
subplot(212)
stem(wk/pi,abs(Sk)/max(abs(Sk)));
xlabel('w/\pi');
ylabel('Sk');
title('FDM信号频域波形')
grid on

 滤波器设计与实现：

clc,clear,close all

% 产生三路调幅信号构成的FDM时域复用信号st
t=0:0.001:1;
fm1=cos(2*pi*30*t);
fm2=cos(2*pi*60*t);
fm3=cos(2*pi*120*t);
f1=cos(2*pi*300*t);
f2=cos(2*pi*600*t);
f3=cos(2*pi*1200*t);
st=fm1.*f1+fm2.*f2+fm3.*f3;
% FDM复用信号st的频谱分析
N=2048;
n=0:N-1;
Fs=4096;
Ts=1/Fs;
fm11=cos(2*pi*30*n*Ts);
fm22=cos(2*pi*60*n*Ts);
fm33=cos(2*pi*120*n*Ts);
f11=cos(2*pi*300*n*Ts);
f22=cos(2*pi*600*n*Ts);
f33=cos(2*pi*1200*n*Ts);
stnT=fm11.*f11+fm22.*f22+fm33.*f33;
Sk=fft(stnT,N);
wk=2*pi/N*n;

% 确定数字滤波器设计指标
ap=0.1; as=60;
Wp1=2*pi*340*Ts; Ws1=2*pi*350*Ts;% 低通
Wp2=[2*pi*500*Ts,2*pi*700*Ts]; Ws2=[2*pi*450*Ts,2*pi*750*Ts];% 带通
Wp3=2*pi*1000*Ts; Ws3=2*pi*950*Ts;% 高通

% 设计滤波器,
[N1,wp1]=ellipord(Wp1/pi,Ws1/pi,ap,as); % 低通
[N2,wp2]=ellipord(Wp2/pi,Ws2/pi,ap,as); % 带通
[N3,wp3]=ellipord(Wp3/pi,Ws3/pi,ap,as); % 高通
[Bz1,Az1]=ellip(N1,ap,as,wp1);  % 低通
[Bz2,Az2]=ellip(N2,ap,as,wp2);  % 带通
[Bz3,Az3]=ellip(N3,ap,as,wp3,'high');   % 高通

% 画损耗函数
[H1,w1]=freqz(Bz1,Az1,1024);
[H2,w2]=freqz(Bz2,Az2,1024);
[H3,w3]=freqz(Bz3,Az3,1024);
subplot(321)
plot(w1/pi,20*log10(abs(H1)/max(abs(H1))));
title('低通滤波器损耗函数')
xlabel('w/\pi');
ylabel('dB');
grid on
subplot(323)
plot(w2/pi,20*log10(abs(H2)/max(abs(H2))));
title('带通滤波器损耗函数')
xlabel('w/\pi');
ylabel('dB');
grid on
subplot(325)
plot(w3/pi,20*log10(abs(H3)/max(abs(H3))));
title('高通滤波器损耗函数')
xlabel('w/\pi');
ylabel('dB');
grid on

% 画信号波形
y1=filter(Bz1,Az1,stnT);  
y2=filter(Bz2,Az2,stnT);
y3=filter(Bz3,Az3,stnT);
subplot(422)
plot(t,st)
xlabel('t');
ylabel('st');
grid on
subplot(424)
plot(n*Ts,y1)
xlabel('t');
ylabel('y1');
grid on
subplot(426)
plot(n*Ts,y2)
xlabel('t');
ylabel('y2');
grid on
subplot(428)
plot(n*Ts,y3)
xlabel('t');
ylabel('y3');
grid on

问题2：根据上述原则，分别给出三个数字滤波器的设计指标wp，ws，αp，αs。

αp = 0.1dB

αs = 60dB

低通：wp=2*340*π*Ts，ws=2*350*π*Ts

带通：wpl=2*500*π*Ts，wsl=2*450*π*Ts；wph=2*700*π*Ts，wsh=2*750*π*Ts

高通：wp=2*1000*π*Ts，ws=2*950*π*Ts

文章来源: blog.csdn.net，作者：渣渣ye，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/yyfloveqcw/article/details/124495448