⭐️前面的话⭐️

大家好！博主开辟了一个新的专栏——剑指offer，我要开始刷题了！这个专栏会介绍《剑指offer》书上所有的面试编程题。并且会分享一些我的刷题心得。由于博主水平有限，如有错误，欢迎指正，如果有更好的解题思路和算法可以分享给博主哦！一起加油！一起努力！

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创！
📆华为云首发时间：🌴2022年4月30日🌴
✉️坚持和努力一定能换来诗与远方！
💭参考书籍：📚《C语言程序设计》📚《剑指offer》
💬参考在线编程网站：🌐牛客网🌐力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🍭作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

⭐️剑指 Offer 16. 数值的整数次方⭐️

🔐题目详情

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，x^n^）。不得使用库函数，同时不需要考虑大数问题。

示例：

输入：x = 2.00000, n = 10
输出：1024.00000
输入：x = 2.10000, n = 3
输出：9.26100
输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

限制：

-100.0 < x < 100.0
-231 <= n <= 231-1
-104 <= x^n <= 104

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/shu-zhi-de-zheng-shu-ci-fang-lcof/

💡解题思路

这道题需要我们实现pow函数，看起来非常简单，其实有坑。
方法1： 直接一次一次地乘。也就是简简单单写一个循环n次的循环，然后每次乘一个x，如果是负数就转换为正数做。但是！！！没这么简单，你在力扣平台提交后超时了！这就说明需要一个更快的算法，使用此方法的时间复杂度为O(N)。所以我们要想出一个优于该方法的算法，也就出现了方法2【快速幂】，它能将时间复杂度降低至O(logN)。

时间复杂度： O(N)

方法2： 快速幂。实现快速幂可以从两个维度考虑，一是二进制角度，二是二分思想角度。

二进制角度解释： 假设需要求x的n次方，也就是x^n^，其中n为整数。对与任何十进制整数，它的二进制序列为b~m~b~m-1~…b~i~…b~2~b~1~，其中0 < i <= m。
将n转换为二进制序列，n = 2^0^*b~1~ + 2^1^*b~2~ + … + 2^i-1^*b~i~ + … + 2^m-1^*b~m~
则

根据以上推导，我们可以拆成两个部分：

1. 求x^1^,x^2^,x^4^,…，这里我们没进行一次计算，就将x=x^2^即可。
2. 求b~1~,b~2~,…,b~i~，这些二进制序列的值，这些好办，因为二进制中，不是0就是1, 可以参考求二进制中1的个数的思路，判断末位是否为1，可以通过n&1 和n>>1实现。

二分思想角度解释： 通过二分的思想，我们可以通过x = x^2^的操作将幂指数n降低至n/2，直到n=0为止。这样相比于一次一次乘效率提高了不少，因为使用单次累乘每进行一次幂指数n降低至n-1，而二分累乘幂指数n降低至n/2。
既然是对幂指数n除2操作，那不得不考虑这个n是奇数还是偶数，如果n为偶数，x^n^ = (x^2^)^n/2^；如果n为奇数x^n^ = (x^2^)^(n-1)/2^ * x。
举个栗子，比如2的10次方，
2^10^ = 4^5^ = 16^2^ * 4 = 256^1^ * 4 = (256*256)^0^ * 256 * 4 = 1024。
3的5次方，
3^5^ = 9^2^ * 3 = 81^1^ * 3 = (81*81)^0^ * 81 * 3 = 243。

最后就是注意当n为负数时，需要将n转换成正数，计算1/x的n次方，但是整型n的取值范围为-2^32^ ~ 2^32^ -1，如果n=-2^32^，去绝对值后n将会整型溢出，所以我们需要将n的值先存入一个长整型变量中，然后使用这个长整形变量进行后续计算就能解决此问题。

时间复杂度： O(logN)

🔑源代码

编程语言：C语言
在线编程平台：力扣

//方法1，超时了
double myPow(double x, int n){
    int i = 0;
    double y = x;
    long m = n;
    if (x == 1)
        return 1.0;
    if (n == 0)
        return 1.0;
    else if (n > 0)
    {
        for (i = 1; i < m; i++)
        {
            x *= y;
        }
        return x;
    }
    else
    {
    	m = -m;
        for (i = 1; i < m; i++)
        {
            x *= y;
        }
        return (1 / x);
    }
}

//方法2
double myPow(double x, int n){
//这道题一个个地乘x会超时，因此使用快速幂的方法实现（二分思想）
    int i = 0;
    double ret = 1.0;
    long m = n;//如果n为最小负数，对n取绝对值后会溢出，所以需要long型变量来储存
    if (x == 1 || n == 0)
        return 1.0;
    if (x == 0)
        return 0;
    if (n < 0)
    {
        m = -m;
        x = 1 / x;
    }
    while (m)
    {
        if (m & 1)
        {
            ret *= x;//如果n为奇数，对结果补乘一个x；如2的5次方可以转换成4的2次方再乘2
        }
        m >>=  1;
        x *= x;
    }
    return ret;
}

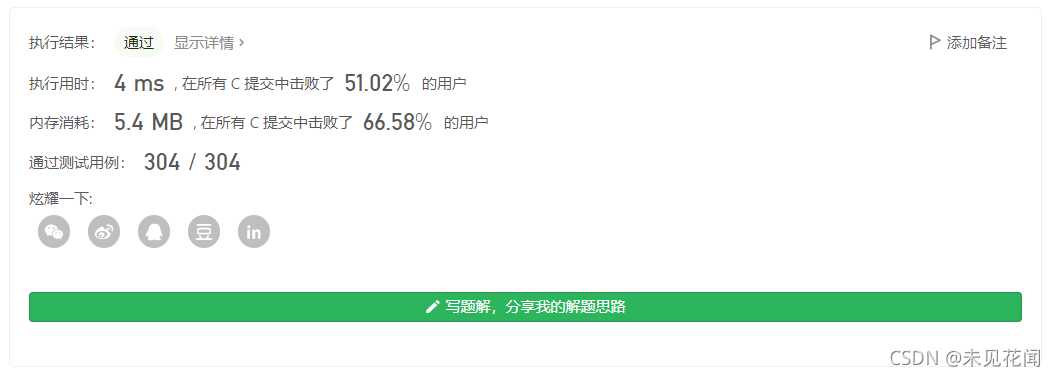
🌱总结

对于pow函数的实现，如果对时间要求更严格，可以从二进制或二分思想入手，实现快速幂。