🍄 前言

🍊这一期我们学习有关C++整数基本应用的知识点和案例🍊

🐳案例一：计算直角三角形的斜边长度

🌱🌱 有一个角为直角的三角形称为直角三角形。在直角三角形中，与直角相邻的两条边称为直角边，直角所对的边称为斜边。直角三角形直角所对的斜边也叫作“弦”。若两条直角边不一样长，短的那条边叫作“勾”，长的那条边叫作“股”。

🌱🌱 勾股定理：如果直角三角形两条直角边分别为a和b，斜边为c，那么a ^ 2 + b ^ 2 = c ^ 2， 即直角三角形两直角边长的平方和等于斜边长的平方。

💦1.1 案例一需求

• 🍒🍒 需求：定义一个函数，通过这函数来计算直角三角形的斜边长度。

• 🍒🍒 案例思路：

  • 🌴 从键盘输入直角三角形的两条直角
  • 🌴 定义一个子函数TriangularHypot
  • 🌴 通过sqrt方法来求直角三角形的斜边
  • 🌴 再去主函数调用我们的子函数TriangularHypot
  • 🌴 输出结果

💦1.2 案例一代码演示

#include <iostream>
#include <math.h>

using namespace std;

double TriangularHypot(float a, float b)
{
    float c;
    c = sqrt(a * a + b * b);
    return c;
}

int main()
{
    //定义两个float的a,b为直角三角形的两条直角边；
    float a, b;
    // 从键盘输入两个治直角边
    cin >> a >> b;
    cout << TriangularHypot(a, b) << endl;
}

💦1.3 案例一运行结果

• 🍒🍒 编译结果：
  

🐳案例二：判断三条边能否构成一个三角形

🌱🌱由同一平面内不在同一直线上的三条线段首尾顺次相接所得的内角和为180度的封闭几何图形叫做三角形，符号为🔺

🌱🌱 三角形定理：三角形任意两边之和大于第三边，任意两边之差小于第三边

💦1.1 案例二需求

• 🍒🍒 需求：定义一个子函数，通过来判断从键盘输入的三条边是否能构成一个三角形。

• 🍒🍒 案例思路：

  • 🌴 从键盘输入直角三角形的三条边
  • 🌴 定义一个子函数TriangleJudge
  • 🌴 通过判断来验证是否能构成一个三角形
  • 🌴 再去主函数调用我们的子函数TriangleJudge
  • 🌴 输出结果

💦1.2 案例二代码演示

#include <iostream>
using namespace std;

bool TriangleJudge(float a, float b, float c)
{
    if((a+b>c)&&(a-b<c))
    {
        if((a+c>b)&&(a-c<b))
        {
            if((b+c>a)&&(b-c<a))
            {
                return true;
            }
            else
            {
                return false;
            }
        }
        else
        {
            return false;
        }
    }
    else
        {
            return false;
        }
}

int main()
{
    float a, b, c;
    // 从键盘分别输入三角形三条边
    cout<<"请输入三角形三条边：" <<endl; 
    cin >> a >> b >> c;
    TriangleJudge(a, b, c) ? (cout << "Yes" << endl) : (cout << "No" << endl);
}

💦1.3 案例二运行结果

• 🍒🍒 输入能构成三角形的三条边时：
  

• 🍒🍒 输入不能构成三角形的三条边时：
  

🐳案例三：定义两个函数来分别求长方形的周长和面积

🌱🌱四个角都是直角的平行四边形叫做长方形，又叫矩形 如下图：

• 🍒🍒其中：长为a，宽为b。则：

  • 🌴 长方形周长（L）公式：长方形周长=（长+宽）×2，即：L = 2 * (a + b)

  • 🌴 长方形面积（S）公式：长方形面积=长×宽，即：S = a * b

💦1.1 案例三需求

• 🍒🍒 需求：定义两个子函数，两个函数分别求长方形的面积和周长。

• 🍒🍒 案例思路：

  • 🌴 从键盘输入长方形的长和宽
  • 🌴 定义一个子函数RectanglePerimeter来计算长方形的周长
  • 🌴 定义另一个子函数RectangleArea来计算长方形的面积
  • 🌴 再去分别调用两个子函数获取周长和面积
  • 🌴 输出结果

💦1.2 案例三代码演示

#include <iostream>

using namespace std;

// 求长方形的周长
int RectanglePerimeter(int a, int b)
{
    int zc;
    zc=(a+b)*2;
    return zc;
}

// 求长方形的面积
int RectangleArea(int a, int b)
{
    int mj;
    mj=a*b;
    return mj;
}


int main()
{
    int a, b;

    cout<<"请输入长方形的长和宽："<<endl;
    // 从键盘输入长方形的长和宽 
    cin >> a >> b;

    cout << "长方形的周长:" << RectanglePerimeter(a,b) << endl;
    cout << "长方形的面积:" << RectangleArea(a,b) << endl;
}

💦1.3 案例三运行结果

• 🍒🍒 输出结果：
  

🐳案例四：定义两个函数来分别求长方形的周长和面积

🌱🌱水仙花数（Narcissistic Number），又称超完全数字不变数、自恋数、自幂数、阿姆斯特朗数。它是指一个n位正整数（n≥3），它的每个数位上的数字的n次幂之和等于它本身（例如：1^3 + 5^3 +3^3=153）。严格来说，3位数的3次幂数才能被视为水仙花数。

💦1.1 案例四需求

• 🍒🍒 需求：定义一个子函数，判断一个三位数是否是水仙花数

• 🍒🍒 案例思路：

  • 🌴 从键盘输入一个三位数
  • 🌴 定义一个子函数NarcissisticNumber来判断该数是不是水仙花数
  • 🌴 再去调用子函数获取子函数的返回值
  • 🌴 输出结果

💦1.2 案例四代码演示

#include <iostream>

using namespace std;

//判断一个三位数是否是水仙花数
bool NarcissisticNumber(int n)
{
    int a=n%10;
    int b=n/10%10;
    int c=n/100;
    if(a*a*a+b*b*b+c*c*c==n)
    {
        return true;
    }
    else
    {
        return false;
    }
   
}


int main()
{
    int n;
    
    // 从键盘输入获取一个三位的整数 
    cout<<"请输入一个三位的整数：" <<endl; 
    cin >> n;

    NarcissisticNumber(n) ? (cout << "Yes" << endl) : (cout << "No" << endl);
}

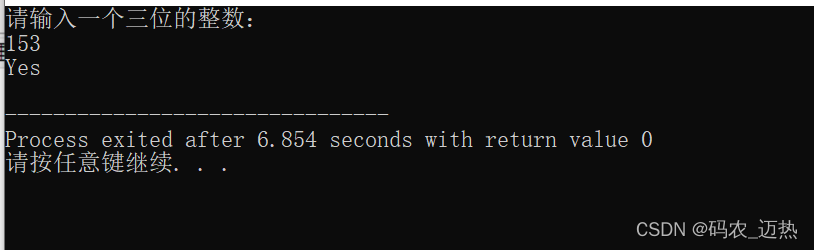
💦1.3 案例四运行结果

• 🍒🍒 正确输入的结果：
  
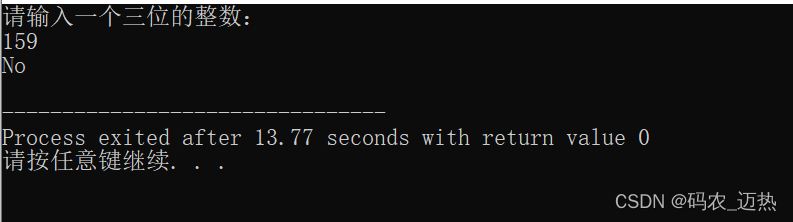
• 🍒🍒输入的不是水仙花数的结果：
  

💻 结语

🍻🍻到这我们的任务就结束啦！！！🌝
感谢大家的阅读 如果在内容方面有什么问题的话可以
在评论区或私信告诉我吧
博主小要求🙏🙏 如果这段对大家有用的话 就给博主
一个免费的点赞👍+评论✉️ +收藏💻吧！！！
感谢大家啦💙💙💙