图

终于树结束了，累坏我了，开始图
如果说树是一对多的话，那么图就是多对多。
都见过地图吧，像陕西就和山西连在了一起，还和内蒙古等等连，典型的多对多

如果说线性表和树的专业术语比较繁琐的话，那么图可能颠覆你的三观，——还有这么多的概念？介于图的概念比较多，我们先来放概念，再讲解

图按照有无方向分为有向图和无向图。有向图由顶点和弧构成，无向图由顶点和边检成。弧有弧尾和弧头之分。

图按照边或须的多少分为稀疏图和稠密图。如果任意两个顶点之间都存在边叫完全图有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。

图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度，有向图顶点分为入度和出度。

图上的边或弧上带权则称为网。

图中顶点间存在路径，两顶点存在路径则说明是连通的，如果路径最终回到起始点则称为环，当中不重复叫简单路径。若任意两顶点都是连通的，则图就是连通图，有向则称强连通图。图中有子图，若子图极大连通则就是连通分量，有向的则称强连通分量。

无向图中连通且n个顶点n-1条边叫生成树。有向图中一顶点入度为0其余顶点入度为1的叫有向树。一个有向图由若干棵有向树构成生成森林。

概念很多，一一刨析

顶点

像树中的结点，聪明的彦祖一下就懂了，就是图中的数据元素嘛，但是有不同之处，线性表中有空表，树中有空树，，但是可没有空图这一说法，why？举个例子：像皇帝的新衣一样，你总不能拿一张纸给别人说只有聪明的人才能看到吧？还有就是在线性表中有线性关系，在树中有层的关系，那么在图中呢？在图中都有关系，一般来说我们将任意俩个顶点的关系用术语边来表示，边的集合可以为空

有向图，无向图

简单的来看就是图上没有箭头就为无向图，反之有箭头为有向图。
如果非要我解释的话，容我先引出无向边和有向边的概念

无向边：反之就是这条边无箭头，如果是A——D，用（A，D）来表示
有向边：简单来说就是这条边有箭头，还是A->D，但是要用<A,D>来表示，注意：不能用<D,A>表示，其中，这条有向边称为弧，A是弧尾，D是弧头也就是说箭头指向的为弧头
那么有向图和无向图就简单了，如果一个图都由有向边组成，则称为有向图，反之为无向图

下面再引出俩个概念：完全有向图，完全无向图，
完全有向图：
在有向图中如果任意俩个顶点都存在方向相反的俩条弧，为完全有向图
完全无向图：
在无向图中任意俩个顶点都存在边相连，则称为完全无向图
还有俩个计算边数的公式为：n*(n-1)/2 and n*(n-1)，猜出来了吧，第一个是计算完全无向图的，第二个是计算完全有向图的
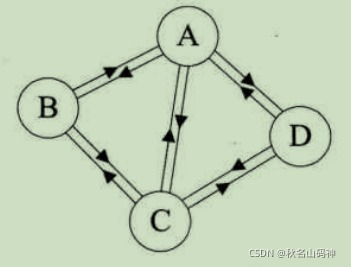
下面我们看俩个图，自己判断一下：


还有个稠密图和稀疏图，都是相对而言的，就像有钱一样，如果我和乞丐比的话，我比较有钱，但是如果我和马云来比的话，可能都没有办法比较。

顶点和边

下面我们把顶点和边串起来讲一下，他们之间也是有联系的

对于无向图来说，当俩个顶点通过一条边相连时，称为顶点相关联，顶点度是和另一个顶点相关联边的条数，顶点可称为互为邻结点
对于有向图来说，如果A->D称为顶点A邻接到顶点D，以A为头的弧为入度，以D为尾的为出度
再来说路径，路径的长度为路径的边或弧的数目，其中第一个顶点和最后一个顶点相同的路径称为回路或环，序列中顶点不重复出现的路径为简单路径，除了第一个顶点和最后一个顶点外，其余顶点不重复出现的回路，又称为简单回路或简单环

连通图

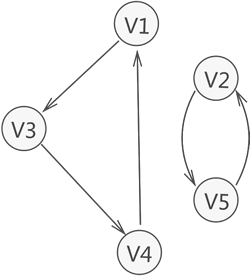
图中从一个顶点到达另一顶点，若存在至少一条路径，则称这两个顶点是连通着的。例如图 1 中，虽然 V1 和 V3 没有直接关联，但从 V1 到 V3 存在两条路径，分别是 V1-V2-V3 和 V1-V4-V3，因此称 V1 和 V3 之间是连通的。

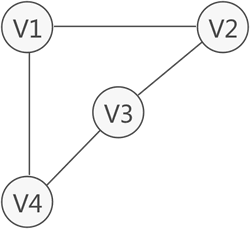
无向图中，如果任意两个顶点之间都能够连通，则称此无向图为连通图。例如，图 2 中的无向图就是一个连通图，因为此图中任意两顶点之间都是连通的。若无向图不是连通图，但图中存储某个子图符合连通图的性质，则称该子图为连通分量。

强连通图
有向图中，若任意两个顶点 Vi 和 Vj，满足从 Vi 到 Vj 以及从 Vj 到 Vi 都连通，也就是都含有至少一条通路，则称此有向图为强连通图。如图 4 所示就是一个强连通图。

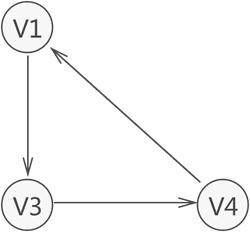
与此同时，若有向图本身不是强连通图，但其包含的最大连通子图具有强连通图的性质，则称该子图为强连通分量。

剩下的就是图有关的算法题了，用例题来说吧

• 图的遍历

给出N个点，M条边的有向图，对于每个点v，求A(v)表示从点v出发，能到达的编号最大的点。

按题目来每次考虑每个点可以到达点编号最大的点，不如考虑较大的点可以反向到达哪些点循环从N到1，则每个点i能访问到的结点的A值都是i
每个点访问一次，这个A值就是最优的，因为之后如果再访问到这个结点那么答案肯定没当前大了

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;

#define MAXL 100010

int N, M, A[MAXL];
vector<int> G[MAXL]; //vector存图 

void dfs(int x, int d) {
	if(A[x]) return; //访问过 
	A[x] = d;
	for(int i=0; i<G[x].size(); i++)
		dfs(G[x][i], d);
}

int main() {
	int u, v;
	scanf("%d%d", &N, &M);
	for(int i=1; i<=M; i++) {
		scanf("%d%d", &u, &v);
		G[v].push_back(u); //反向建边 
	}
	for(int i=N; i; i--) dfs(i, i); 
	for(int i=1; i<=N; i++) printf("%d ", A[i]);
	printf("\n");
	return 0;
}

• 邻接矩阵
  给定一个整数矩阵
  

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
const int Len = 200 * 200 * 5 + 5,Inf = 1e9;
int dep[Len],cnt = 1,head[Len],s,t,S,T,cur[Len],val[Len],a[205][205],sumh[205],suml[205],LL,RR,n,m,sum,ans,minn;
struct node
{
	int next,to,w;
}edge[Len << 1];
void add(int from,int to,int w)
{
	edge[++ cnt].to = to;
	edge[cnt].w = w;
	edge[cnt].next = head[from];
	head[from] = cnt;
}
int BFS()
{
	queue<int> q;
	memset(dep , 0 , sizeof dep);
	q.push(S);dep[S] = 1;cur[S] = head[S];
	while(!q.empty())
	{
		int p = q.front() ; q.pop();
		for(int e = head[p] ; e ; e = edge[e].next)
		{
			int to = edge[e].to;
			if(!dep[to] && edge[e].w)
			{
				dep[to] = dep[p] + 1;
				cur[to] = head[to];
				if(T == to) return dep[T];
				q.push(to);
			}
		}
	}
	return dep[T];
}
int dfs(int u,int In)
{
	if(u == T) return In;
	int Out = 0;
	for(int e = cur[u] ; e && In > 0 ; e = edge[e].next)
	{
		cur[u] = e;
		int to = edge[e].to;
		if(edge[e].w && dep[to] == dep[u] + 1)
		{
			int res = dfs(to , min(In , edge[e].w));
			In -= res;
			Out += res;
			edge[e].w -= res;
			edge[e ^ 1].w += res; 
		}
	}
	return (!Out) ? dep[u] = 0 : Out;
}
int Clone(int x,int y){return (x - 1) * n + y;}
bool check(int res)
{
	memset(head , 0 , sizeof head) ; cnt = 1;
	memset(val , 0 , sizeof val);
	sum = ans = 0;
	for(int i = 1 ; i < n ; i ++)//处理行
	{
		int now = Clone(i , m) , L = sumh[i] - res , R = sumh[i] + res;//L = sumh[i] - res , R = sumh[i] + res
		add(s , now , R - L) , add(now , s , 0);
		val[now] += L , val[s] -= L;
	}
	for(int i = 1 ; i < m ; i ++)
	{
		int now = Clone(n , i) , L = suml[i] - res , R = suml[i] + res;
		add(now , s , R - L) , add(s , now , 0);
		val[s] += L , val[now] -= L; 
	}
	for(int i = 1 ; i < n ; i ++)
	{
		int now = Clone(i , m);
		for(int j = 1 ; j < m ; j ++)
		{
			int to = Clone(i , j);
			add(now , to , RR - LL) , add(to , now , 0);
			val[to] += LL , val[now] -= LL; 
		}
	} 
	for(int i = 1 ; i < m ; i ++)
	{
		int now = Clone(n , i);
		for(int j = 1 ; j < n ; j ++)
		{
			int to = Clone(j , i);
			add(to , now , RR - LL) , add(now , to , 0);
			val[now] += LL , val[to] -= LL;
		}
	}
	for(int i = 1 ; i <= n * m + 1 ; i ++)
	{
		if(val[i] > 0) add(S , i , val[i]) , add(i , S , 0) , sum += val[i];
		if(val[i] < 0) add(i , T , -val[i]) , add(T , i , 0);
	}
	while(BFS()) ans += dfs(S , Inf);
	if(ans == sum) return true;
	return false;
}
signed main()
{
	minn = 1e9;
	scanf("%d %d",&n,&m);
	n ++ , m ++;
	s = n * m , t = n * m + 1 , S = n * m + 2 , T = n * m + 3; 
	for(int i = 1 ; i <= n - 1 ; i ++)
		for(int j = 1 ; j <= m - 1 ; j ++) 
		{
			scanf("%d",&a[i][j]);
			sumh[i] += a[i][j] , suml[j] += a[i][j];
		}
	for(int i = 1 ; i <= n - 1 ; i ++) minn = min(minn , sumh[i]);
	for(int i = 1 ; i <= m - 1 ; i ++) minn = min(minn , suml[i]);
	scanf("%d %d",&LL,&RR);
	int l = 0 , r = minn,anss;
	while(l <= r)
	{
		int mid = (l + r) >> 1;
		if(check(mid)) anss = mid , r = mid - 1;
		else l = mid + 1; 
	}
	printf("%d\n",anss);
	return 0;
}

来自：矩阵

再来一个深搜结束吧

• 深度优先遍历
  给出N个点，M条边的有向图，对于每个点v，求A(v)表示从点v出发，能到达的编号最大的点

比较简单：反向建边 + dfs
按题目来每次考虑每个点可以到达点编号最大的点，不如考虑较大的点可以反向到达哪些点循环从N到1，则每个点i能访问到的结点的A值都是i每个点访问一次，这个A值就是最优的，因为之后如果再访问到这个结点那么答案肯定没当前大了

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;

#define MAXL 100010

int N, M, A[MAXL];
vector<int> G[MAXL]; //vector存图 

void dfs(int x, int d) {
	if(A[x]) return; //访问过 
	A[x] = d;
	for(int i=0; i<G[x].size(); i++)
		dfs(G[x][i], d);
}

int main() {
	int u, v;
	scanf("%d%d", &N, &M);
	for(int i=1; i<=M; i++) {
		scanf("%d%d", &u, &v);
		G[v].push_back(u); //反向建边 
	}
	for(int i=N; i; i--) dfs(i, i); 
	for(int i=1; i<=N; i++) printf("%d ", A[i]);
	printf("\n");
	return 0;
}

深搜有了，不上广搜有点过意不去，算了再来个广搜

• 广搜
  有一个 n×m 的棋盘，在某个点 (x,y) 上有一个马，要求你计算出马到达棋盘上任意一个点最少要走几步。

#include<iostream>//P1443
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<queue>//运用了队列
#include<cmath>
using namespace std;
const int dx[8]={-1,-2,-2,-1,1,2,2,1};
const int dy[8]={2,1,-1,-2,2,1,-1,-2};//8个方向
queue<pair<int,int> > q;
int f[500][500];//存步数
bool vis[500][500];//走没走过
int main()
{
	int n,m,x,y;
	memset(f,-1,sizeof(f));memset(vis,false,sizeof(vis));
	cin>>n>>m>>x>>y;
	f[x][y]=0;vis[x][y]=true;q.push(make_pair(x,y));
	while(!q.empty())
	{
		int xx=q.front().first,yy=q.front().second;q.pop();//取队首并出队
		for(int i=0;i<8;i++)
		{
			int u=xx+dx[i],v=yy+dy[i];
			if(u<1||u>n||v<1||v>m||vis[u][v])continue;//出界或走过就不走
		    vis[u][v]=true;q.push(make_pair(u,v));f[u][v]=f[xx][yy]+1;
		}
	}
	for(int i=1;i<=n;i++)
	 {for(int j=1;j<=m;j++)printf("%-5d",f[i][j]);printf("\n");}//注意场宽！！
	return 0;
}

• 最短路径
  实际上对于最短路径，让我看的话，它和深搜，广搜差不多
  主要是这俩个大佬发明的东西

• 迪杰斯特拉算法

• 弗洛伊德算法

下面就按顺序来看一下
Dijkstra算法采用的是一种贪心的策略，声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合：T，初始时，原点 s 的路径权重被赋为 0 （dis[s] = 0）。若对于顶点 s 存在能直接到达的边（s,m），则把dis[m]设为w（s, m）,同时把所有其他（s不能直接到达的）顶点的路径长度设为无穷大。初始时，集合T只有顶点s。然后，从dis数组选择最小值，则该值就是源点s到该值对应的顶点的最短路径，并且把该点加入到T中，OK，此时完成一个顶点，然后，我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短，如果是，那么就替换这些顶点在dis中的值。最后，又从dis中找出最小值，重复上述动作，直到T中包含了图的所有顶点。
这个总体上是一个：广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树

#pragma once
#include<iostream>
#include<string>
using namespace std;

//邻接矩阵保存
//记录起点到每个顶点的最短路径的信息
struct Dis {
    string path;
    int value;
    bool visit;
    Dis() {
        visit = false;
        value = 0;
        path = "";
    }
};

class Graph_DG {
private:
    int vexnum;   //图的顶点个数
    int edge;     //图的边数
    int **arc;   //邻接矩阵
    Dis * dis;   //记录各个顶点最短路径的信息
public:
    //构造函数
    Graph_DG(int vexnum, int edge);
    //析构函数
    ~Graph_DG();
    // 判断我们每次输入的的边的信息是否合法
    //顶点从1开始编号
    bool check_edge_value(int start, int end, int weight);
    //创建图
    void createGraph();
    //打印邻接矩阵
    void print();
    //求最短路径
    void Dijkstra(int begin);
    //打印最短路径
    void print_path(int);
};

#include"Dijkstra.h"

//构造函数
Graph_DG::Graph_DG(int vexnum, int edge) {
    //初始化顶点数和边数
    this->vexnum = vexnum;
    this->edge = edge;
    //为邻接矩阵开辟空间和赋初值
    arc = new int*[this->vexnum];
    dis = new Dis[this->vexnum];
    for (int i = 0; i < this->vexnum; i++) {
        arc[i] = new int[this->vexnum];
        for (int k = 0; k < this->vexnum; k++) {
            //邻接矩阵初始化为无穷大
                arc[i][k] = INT_MAX;
        }
    }
}
//析构函数
Graph_DG::~Graph_DG() {
    delete[] dis;
    for (int i = 0; i < this->vexnum; i++) {
        delete this->arc[i];
    }
    delete arc;
}

// 判断我们每次输入的的边的信息是否合法
//顶点从1开始编号
bool Graph_DG::check_edge_value(int start, int end, int weight) {
    if (start<1 || end<1 || start>vexnum || end>vexnum || weight < 0) {
        return false;
    }
    return true;
}

void Graph_DG::createGraph() {
    cout << "请输入每条边的起点和终点（顶点编号从1开始）以及其权重" << endl;
    int start;
    int end;
    int weight;
    int count = 0;
    while (count != this->edge) {
        cin >> start >> end >> weight;
        //首先判断边的信息是否合法
        while (!this->check_edge_value(start, end, weight)) {
            cout << "输入的边的信息不合法，请重新输入" << endl;
            cin >> start >> end >> weight;
        }
        //对邻接矩阵对应上的点赋值
        arc[start - 1][end - 1] = weight;
        //无向图添加上这行代码
        //arc[end - 1][start - 1] = weight;
        ++count;
    }
}

void Graph_DG::print() {
    cout << "图的邻接矩阵为：" << endl;
    int count_row = 0; //打印行的标签
    int count_col = 0; //打印列的标签
    //开始打印
    while (count_row != this->vexnum) {
        count_col = 0;
        while (count_col != this->vexnum) {
            if (arc[count_row][count_col] == INT_MAX)
                cout << "∞" << " ";
            else
            cout << arc[count_row][count_col] << " ";
            ++count_col;
        }
        cout << endl;
        ++count_row;
    }
}
void Graph_DG::Dijkstra(int begin){
    //首先初始化我们的dis数组
    int i;
    for (i = 0; i < this->vexnum; i++) {
        //设置当前的路径
        dis[i].path = "v" + to_string(begin) + "-->v" + to_string(i + 1);
        dis[i].value = arc[begin - 1][i];
    }
    //设置起点的到起点的路径为0
    dis[begin - 1].value = 0;
    dis[begin - 1].visit = true;

    int count = 1;
    //计算剩余的顶点的最短路径（剩余this->vexnum-1个顶点）
    while (count != this->vexnum) {
        //temp用于保存当前dis数组中最小的那个下标
        //min记录的当前的最小值
        int temp=0;
        int min = INT_MAX;
        for (i = 0; i < this->vexnum; i++) {
            if (!dis[i].visit && dis[i].value<min) {
                min = dis[i].value;
                temp = i;
            }
        }
        //cout << temp + 1 << "  "<<min << endl;
        //把temp对应的顶点加入到已经找到的最短路径的集合中
        dis[temp].visit = true;
        ++count;
        for (i = 0; i < this->vexnum; i++) {
            //注意这里的条件arc[temp][i]!=INT_MAX必须加，不然会出现溢出，从而造成程序异常
            if (!dis[i].visit && arc[temp][i]!=INT_MAX && (dis[temp].value + arc[temp][i]) < dis[i].value) {
                //如果新得到的边可以影响其他为访问的顶点，那就就更新它的最短路径和长度
                dis[i].value = dis[temp].value + arc[temp][i];
                dis[i].path = dis[temp].path + "-->v" + to_string(i + 1);
            }
        }
    }

}
void Graph_DG::print_path(int begin) {
    string str;
    str = "v" + to_string(begin);
    cout << "以"<<str<<"为起点的图的最短路径为：" << endl;
    for (int i = 0; i != this->vexnum; i++) {
        if(dis[i].value!=INT_MAX)
        cout << dis[i].path << "=" << dis[i].value << endl;
        else {
            cout << dis[i].path << "是无最短路径的" << endl;
        }
    }
}

#include"Dijkstra.h"


//检验输入边数和顶点数的值是否有效，可以自己推算为啥：
//顶点数和边数的关系是：((Vexnum*(Vexnum - 1)) / 2) < edge
bool check(int Vexnum, int edge) {
    if (Vexnum <= 0 || edge <= 0 || ((Vexnum*(Vexnum - 1)) / 2) < edge)
        return false;
    return true;
}
int main() {
    int vexnum; int edge;

    cout << "输入图的顶点个数和边的条数：" << endl;
    cin >> vexnum >> edge;
    while (!check(vexnum, edge)) {
        cout << "输入的数值不合法，请重新输入" << endl;
        cin >> vexnum >> edge;
    }
    Graph_DG graph(vexnum, edge);
    graph.createGraph();
    graph.print();
    graph.Dijkstra(1);
    graph.print_path(1);
    system("pause");
    return 0;
}

弗洛伊德算法，我就使用伪代码来写了，

//总体上是一个二重循环加上一个三重循环，主要运用于所有顶点到所有顶点的最短路径问题
void ShortestPath FLOYD(MGraph G, PathMatrix &p[], DistanceMatrix &D){
	//用Floyd算法求有向网中各对顶点v和w之间的最短路径P[v][w]及其带权长
	//度D[v][w].若P[v][w][u]为TRUE,则u是从v到w当前求得最短路径上的顶点。
	for(v = 0; v < G.vexnum; ++v)		//各对结点之间初始已知路径及距离
		for(w = 0; w < G.vexnum; ++w){
			D[v][w] = G.arcs[v][w];
			for(u = 0; u < G.vexnum; ++w)	P[v][w][u] = FALSE;
			if(D[v][w] < INFINITY){				//从v到w有直接路径
				P[v][w][v] = TRUE; P[v][w][w] = TRUE;
			}//if
		}//for
	
	for(u = 0; u < G.vexnum; ++u)
		for(v = 0; v<G.vexnum; ++v)
			for(w = 0; w<G.vexnum; ++w)
				if(D[v][u] + D[u][w] < D[v][w]){		//从v经u到w的一条路径更短
					D[v][w] = D[v][u] + D[u][w];
					for(i = 0; i<G.vexnum; ++i)
						P[v][w][i] = P[v][u][i] || P[u][w][i];
						}//if
}//ShortestPath.FLOYD

图用网上十分流行的一句话来结尾，
世界上最遥远的距离是我找不到与你的最短路径 ， 哭了

最后

码神，肝了一个周的时间，算是把数据结构肝完了吧，算法如果要展开来讲的话，感觉10w字都拦不住，数据结构就到这吧，原创不易，希望支持，如果有想看我手撕《🗡 ☞offer》或者更python还是java的，欢迎留言，我抽剩下的半个月来肝一个完整版。还有就是如果有哪一块写的有问题也欢迎指出！
最后感谢大家的支持，想要一个关注！点赞，评论！