- 微信
- 微博
  
  分享文章到微博
- 复制链接
  
  复制链接到剪贴板

码神爆肝数据结构——总长5w字，附带例题（下）

秋名山码民发表于 2022/04/27 13:20:21 2022/04/27

【摘要】树终于摆脱线性表了，线性表是一对一，但是树就不一样了，一对多的性质扑面而来，先看一下百度的说法吧，树：它是由n(n≥1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。就用这张图来描述树的特征：当n=0，就称为空树有且只有一个称为根的结点，这里为A当n>1时，其余结点可以分为m(m>0)个互不相交的有限集，其中每个集合又是一...

树

终于摆脱线性表了，线性表是一对一，但是树就不一样了，一对多的性质扑面而来，先看一下百度的说法吧，
树：它是由n(n≥1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

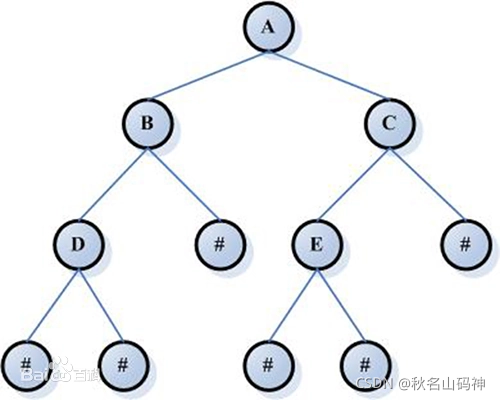
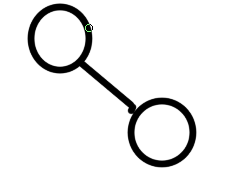
就用这张图来描述树的特征：

当n=0，就称为空树
有且只有一个称为根的结点，这里为A
当n>1时，其余结点可以分为m(m>0)个互不相交的有限集，其中每个集合又是一棵树，称为子树
举个例子：
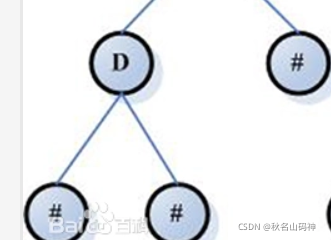
是以B为结点的子树

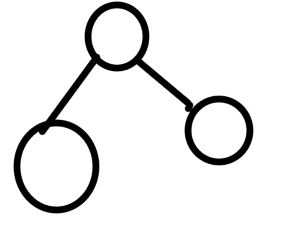
下面我们来将结点分一下类：

树的结点包含一个数据结构及若干指向其子树的分支
结点拥有的子树称为结点的度
度为0的结点称为叶结点或终端结点
度不为0的结点称为非终端结点或分支结点
看图

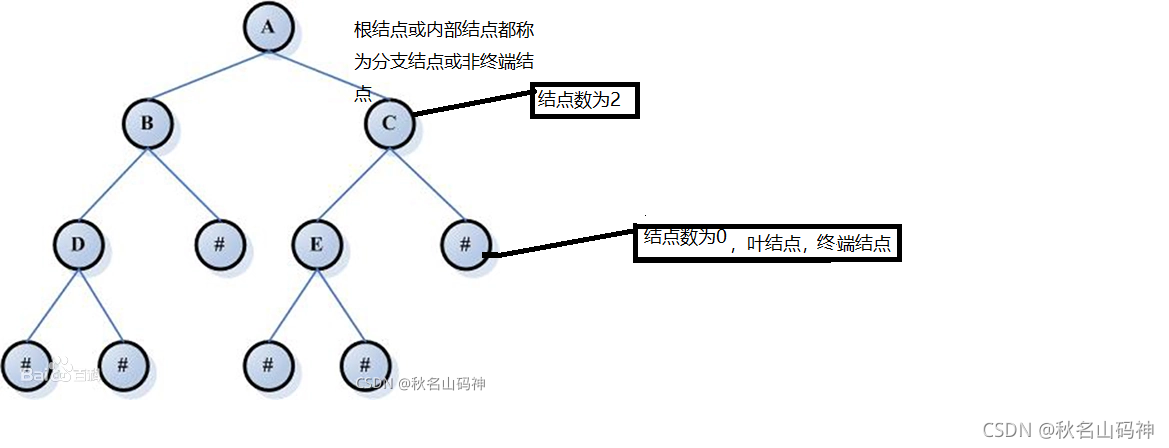
结点的关系：
这块有点像我们的家庭关系，比较好理解
像上图A为B，C的双亲，B，C互为兄弟，对于#来说，D，B，A，都是它的祖先，反之A的子孙有B，D，#

其他相关概念，特定情况才会用到

引入了深度，可以说是有几层就有多少深度.
无序树：如果将树中结点的各子树看成从左到右都是没有次序，都可以随意互换，则称为无序树，反之为有序树

树的基本操作

双亲表示法

树真的太像人了，人可能暂时没有孩子但是一定有且只有一个父母，树也一样除了根结点外，其余每个结点，它不一定有孩子，但是一定有且只有一个双亲

/*
Project: Tree_parent(树-双亲表示法)
Date:    2019/02/25
Author:  Frank Yu
基本操作函数：
InitTree(Tree &T) 参数T，树根节点 作用：初始化树，先序递归创建
InsertNode(Tree &T, TElemType node) 插入树的结点 参数：树T,结点node 作用：在双亲数组中插入结点，增加树的结点值
InsertParent(Tree &T, TElemType node1, TElemType node2)//插入双亲数组的双亲域 参数：树T ，结点node1,结点node2
                                                       //作用：使双亲数组中,node2对应的双亲域为node1的下标
GetIndegree(Tree &T, TElemType node)                   //得到某结点入度 参数：树T，结点node 结点不存在返回-1
GetOutdegree(Tree &T, TElemType node)                  //得到某结点出度 参数：树T，结点node 结点不存在返回-1
PreOrder(Tree T)  参数：树T,根节点下标 作用：先序遍历树
PostOrder(Tree T) 参数：树T,根节点下标 作用：后序遍历树
LevelOrder(Tree T)参数：树T            作用：层序遍历树
功能实现函数：
CreateTree(Tree &T) 参数T，树根节点 作用：创建树，调用InsertNode,InsertParent
Traverse(Tree T)    参数T，树根节点 作用：PreOrder InOrder PostOrder LevelOrder遍历树
*/
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<string>
#include<stack>
#include<queue>
#include<algorithm>
#include<iostream>
#define TElemType char
#define Max 100
using namespace std;
//树的结点数据结构
typedef struct TNode
{
	TElemType data;//数据域
	int parent;    //双亲
}TNode;
//树的数据结构
typedef struct Tree
{
 
	TNode parent[Max];
	int NodeNum;
 
}Tree;
//********************************基本操作函数********************************//
//初始化树函数 参数：树T 作用：规定数据域为#，则为空，双亲为-1,则为空
void InitTree(Tree &T)
{
	for (int i=0;i<Max;i++)
	{
		T.parent[i].data = '#';
		T.parent[i].parent = -1;
	}
	T.NodeNum = 0;
}
//插入树的结点 参数：树T,结点node 作用：在双亲数组中插入结点，增加树的结点值
bool InsertNode(Tree &T, TElemType node)
{
	
	if (node != '#')
	{
		T.parent[T.NodeNum++].data = node;//插入到双亲数组中
		return true;
	}
	return false;
}
//插入双亲数组的双亲域 参数：树T ，结点node1,结点node2
//作用：使双亲数组中,node2对应的双亲域为node1的下标
bool InsertParent(Tree &T, TElemType node1, TElemType node2)
{
	int place1, place2;
	place1 = -1;place2 = -1;
	for (int i=0;i<T.NodeNum;i++)//查找两点是否存在
	{
		if (node1 == T.parent[i].data)place1 = i;
		if (node2 == T.parent[i].data)place2 = i;
	}
	if (place1 != -1 && place2 != -1)//两点均存在
	{
		T.parent[place2].parent = place1;
		return true;
	}
	return false;
}
//得到某结点入度 参数：树T，结点node 结点不存在返回-1
int GetIndegree(Tree &T, TElemType node)
{
	int place = -1;
	for (int i = 0;i<T.NodeNum;i++)
	{
		if (T.parent[i].data == node)place = i;
	}
	if (place!=-1)//结点存在
	{
		if(T.parent[place].parent!=-1)return 1;//双亲只能有一个
		else return 0; //根节点没有双亲，即没有入度
	}
	return -1;
}
//得到某结点出度 参数：树T，结点node 结点不存在返回-1
int GetOutdegree(Tree &T, TElemType node)
{
	int place = -1;
	int outdegree = 0;
	for (int i = 0;i<T.NodeNum;i++)
	{
		if (T.parent[i].data == node)place = i;
	}
	if (place != -1)
	{
		for (int i = 0;i < T.NodeNum;i++)
		{
			if (T.parent[i].parent == place)outdegree++;
		}
		return outdegree;
	}
	return -1;
}
//先序遍历 参数：树T,根节点下标
void PreOrder(Tree T,int i)
{
	if (T.NodeNum != 0)
	{
		cout << T.parent[i].data << " ";
		for(int j=0;j<T.NodeNum;j++)
		{
		  if(T.parent[j].parent==i)
		  PreOrder(T,j);//按左右先序遍历子树
		}
	}
}
//后序遍历 参数：树T,根节点下标
void PostOrder(Tree T,int i)
{
	if (T.NodeNum != 0)
	{
		
		for (int j = 0;j<T.NodeNum;j++)
		{
			if (T.parent[j].parent == i)
				PostOrder(T, j);//按左右先序遍历子树
		}
		cout << T.parent[i].data << " ";
	}
}
//层序遍历 参数：树T
void LevelOrder(Tree T)
{
	queue<TNode> q;//借助队列
	if (T.NodeNum!=0)
	{
		TNode temp;//暂存要出队的结点
		q.push(T.parent[0]);//根结点入队
		while (!q.empty())//队列非空
		{
			temp = q.front();
			q.pop();
			cout<<temp.data<<" ";
			for (int j = 0;j<T.NodeNum;j++)
			{
				if (T.parent[T.parent[j].parent].data == temp.data)//当前结点的父节点的数据域与弹出的相同 
					//因为temp没有保存下标，只能按这种方式比较，默认结点名称不同
					q.push(T.parent[j]);//队列先进先出，先入左孩子
			}
		}
	}
}
//**********************************功能实现函数*****************************//
//创建树，调用InsertNode,InsertParent
void CreateTree(Tree &T)
{
	int nodenum = 0;
	int parent;
	TElemType node,node1,node2;
	printf("请输入树的结点个数:");
	cin >> nodenum;
	parent = nodenum - 1;
	printf("请输入树的结点名称（空格隔开）:");
	while (nodenum--)
	{
		cin >> node;
		InsertNode(T,node);
	}
	printf("请输入树的结点间的双亲关系（一对为一双亲关系，A B表示A为B的双亲）:\n");
	while (parent--)
	{
		cin >> node1>>node2;
		InsertParent(T,node1,node2);
	}
	printf("\n");
}
//入度
void Indegree(Tree &T)
{
	TElemType node;
	int indegree;
	printf("请输入结点名称:\n");
	cin >> node;
	indegree = GetIndegree(T, node);
	if (-1 != indegree)
		cout << "该结点入度为：" << indegree << endl;
	else
		cout << "结点不存在。" << endl;
}
//出度
void Outdegree(Tree &T)
{
	TElemType node;
	int outdegree;
	printf("请输入结点名称:\n");
	cin >> node;
	outdegree = GetOutdegree(T, node);
	if (-1 != outdegree)
		cout << "该结点出度为：" << outdegree << endl;
	else
		cout << "结点不存在。" << endl;
}
//遍历功能函数 调用PreOrder InOrder PostOrder LevelOrder
void Traverse(Tree T)
{
	int choice;
	while (1)
	{
		printf("********1.先序遍历    2.后序遍历*********\n");
		printf("********3.层次遍历    4.返回上一单元*********\n");
		printf("请输入菜单序号：\n");
		scanf("%d", &choice);
		if (4 == choice) break;
		switch (choice)
		{
		case 1: {printf("树先序遍历序列:");PreOrder(T,0);printf("\n");}break;
		case 2: {printf("树后序遍历序列:");PostOrder(T,0);printf("\n");}break;
		case 3: {printf("树层序遍历序列:");LevelOrder(T);printf("\n");}break;
		default:printf("输入错误！！！\n");break;
		}
	}
}
//菜单
void menu()
{
	printf("********1.创建     2.某点入度*********\n");
	printf("********3.某点出度 4.遍历*************\n");
	printf("********5.退出\n");
}
//主函数
int main()
{
	Tree T;
	int choice = 0;
	InitTree(T);
	while (1)
	{
		menu();
		printf("请输入菜单序号：\n");
 
		scanf("%d", &choice);
		if (5 == choice) break;
		switch (choice)
		{
		case 1:CreateTree(T);break;
		case 2:Indegree(T);break;
		case 3:Outdegree(T);break;
		case 4:Traverse(T);break;
		default:printf("输入错误！！！\n");break;
		}
	}
	return 0;
}

所用图

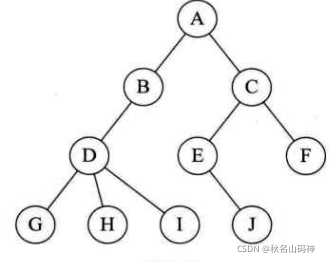
孩子表示法

顾名思义，就是每个结点有多个指针域，其中每个指针指向一棵子树的根结点，我们也把这种方法叫做多重链表表式法，有点像线性表中的链式表示法
那么这样的话，我这里就写伪代码了

//指针域的个数就等于树的度，其中树的度又等于树各个结点度的最大值
struct ChildNode
{
	int data；
	ChildNode*;
}
ChildNode *D;//d为最大结点
d.ChildNode;

不难看出这样的话，如果各个树度之间的差距不大，还可以，但是如果各个树度之间的差距很大，那么很浪费空间，原因是许多的结点域都是空的

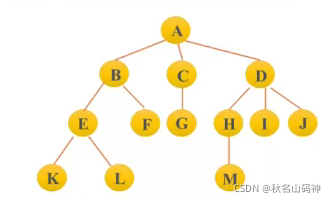
孩子兄弟表示法

这个可以说是学二叉树的基础，有的兄弟可能要说了，为什么不是兄弟表示法？还要带上我的孩子一起？
因为可能存在下面这种情况，只有了兄弟，孩子没有办法往下延申了，那么如何孩子和兄弟一起开呢？
是这样的，任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在也是唯一的，记得不是堂兄弟昂，是亲兄弟，下面我们看图

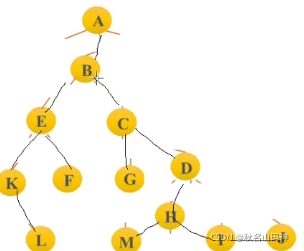
观察后，我们可以发现每个结点最多有俩个孩子，也就是一个简单的二叉树，这也可以说是，孩子兄弟表示法最大的好处

struct Node
{
	int data;
	*firstchild,*ringtsib;
}
Node *Tree;

二叉树

恶魔来了，有关二叉树及其衍生的东西往往是树中的难点，下面来个大家讲个故事：还是以前的小苗，话说我以前刚看上小苗时，几乎没有人知道，但是我对我的兄弟说我看上了一个女孩，让他猜，但是我每次只回答”对“或”错“，然后就相当于降低了难度莫，身高，体重，魅力，头发等等，都可以用一个人来比较，这样的话又降低了难度，二叉树也是一样的，只不过它是通过比较大小来降低难度的，下面我们回归正题
特点：

每个结点最多有俩棵子树
左右子树都是有顺序的，不能任意颠倒
即使只有一棵子树，也要区分它是左子树还是右子树

一般情况下，有以下几种基本形态

空二叉树，没有办法画图了
只有一个根结点
根结点只有左子树
根结点只有右子树
根结点既有左子树又有右子树
再思考一下，如果有三个结点的二叉树，又有几种形态呢？
5种，怎么来的？先看图

由于他必须是有序的所以要单个计算，左右分开，加起来就是5种
下面来说几个特殊的二叉树：
满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。
完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。
斜树：有点像线性表，这个斜可以不分左右，所以更像线性表了

如何判断完全二叉树，下面是它的特征：

叶子结点只能出现在最下俩层、
最下层的叶子一定集中在左部的连续位置
倒数俩层，若有叶子结点，一定都在右部连续位置
如果结点度为一，则该结点只有左孩子
同样结点数的二叉树，完全二叉树的深度最小

下面我们来看一下，二叉树的存储结构吧，也分为顺序存储和链式存储

顺序存储

由于树是一对多的关系，顺序存储实现有点困难，但是二叉树是一种特殊的树，由于它的特殊性，顺序存储可以实现。
顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

链表存储

由于二叉树每个结点最多有俩个孩子，所以给它设计一个数据域和俩个指针域，组成二叉链表

 struct BinaryTreeNode
   {
    struct BinTreeNode* _pLeft; // 指向当前节点左孩子
    struct BinTreeNode* _pRight; // 指向当前节点右孩子
    BTDataType _data; // 当前节点值域
   }

BinaryTreeNode *tree;

遍历二叉树

所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。从而引出了次序问题，像码神刚刚结束的高考志愿问题，哪个城市，哪个学校，哪个专业，或者那个她，由于选择不同，所以最后的遍历次序也截然不同。
方法：

前序遍历——访问根结点的操作发生在遍历其左右子树之前。
从根开始先左后右
中序遍历——访问根结点的操作发生在遍历其左右子树之中。
中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树
后序遍历——访问根结点的操作发生在遍历其左右子树之后。
从左到右先子叶后结点的方式遍历访问左右子树，最后是根结点
层序遍历——设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;




typedef BTNode* QDataType;
// 链式结构：表示队列 
typedef struct QListNode
{
	struct QListNode* _next;
	QDataType _data;
}QNode;

// 队列的结构 
typedef struct Queue
{
	QNode* _front;
	QNode* _rear;
}Queue;




BTNode* CreateBTNode(BTDataType x);
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);







// 初始化队列 
void QueueInit(Queue* q);
// 队尾入队列 
void QueuePush(Queue* q, QDataType data);
// 队头出队列 
void QueuePop(Queue* q);
// 获取队列头部元素 
QDataType QueueFront(Queue* q);
// 获取队列队尾元素 
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数 
int QueueSize(Queue* q);
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q);
// 销毁队列 
void QueueDestroy(Queue* q);



// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);

// 初始化队列 
void QueueInit(Queue* q)
{
	assert(q);
	q->_front = q->_rear = NULL;
}
// 队尾入队列 
void QueuePush(Queue* q, QDataType data)
{
	assert(q);
	QNode *newnode = ((QNode*)malloc(sizeof(QNode)));
	newnode->_data = data;
	newnode->_next = NULL;
	if (q->_rear == NULL)
	{
		q->_front = q->_rear = newnode;
	}
	else
	{
		q->_rear->_next = newnode;
		//q->_rear = q->_rear->_next;
		q->_rear = newnode;
	}
}
// 队头出队列 
void QueuePop(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	if (q->_front == q->_rear)
	{
		free(q->_front);
		//free(q->_rear);
		q->_front = q->_rear = NULL;
	}
	else
	{
		QNode *cur = q->_front->_next;
		free(q->_front);
		q->_front = cur;
	}
}
// 获取队列头部元素 
QDataType QueueFront(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	return q->_front->_data;
}
// 获取队列队尾元素 
QDataType QueueBack(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	return q->_rear->_data;
}
// 获取队列中有效元素个数 
int QueueSize(Queue* q)
{
	assert(q);
	int size = 0;
	QNode* cur = q->_front;
	while (cur)
	{
		++size;
		cur = cur->_next;
	}
	return size;
}
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q)
{
	assert(q);
	return q->_front == NULL ? 1 : 0;
}
// 销毁队列 
void QueueDestroy(Queue* q)
{
	assert(q);
	QNode *cur = q->_front;
	while (cur)
	{
		QNode *next = cur->_next;
		free(cur);
		cur = next;
	}
	q->_front = q->_rear = NULL;
}






BTNode* CreateBTNode(BTDataType x)
{
	BTNode *node = (BTNode*)malloc(sizeof(BTNode));
	node->_data = x;
	node->_left = NULL;
	node->_right = NULL;
	return node;
}


// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
	if (a[*pi] == '#')
	{
		return NULL;
	}
	BTNode *node = (BTNode*)malloc(sizeof(BTNode));
	node->_data = a[*pi];
	++*pi;
	node->_left = BinaryTreeCreate(a, n, pi);
	++*pi;
	node->_right = BinaryTreeCreate(a, n, pi);
	return node;
}
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{
	if (*root != NULL)
	{
		if ((*root)->_left) // 有左孩子
			BinaryTreeDestory(&(*root)->_left); // 销毁左孩子子树
		if ((*root)->_right) // 有右孩子
			BinaryTreeDestory(&(*root)->_right); // 销毁右孩子子树

		free(*root); // 释放根结点
		*root = NULL; // 空指针赋NULL
	}
}
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->_left == NULL&&root->_right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->_data == x)
	{
		return root;
	}
	BTNode* ret=BinaryTreeFind(root->_left,x);
	if (ret != NULL)
	{
		return ret;
	}
	ret = BinaryTreeFind(root->_right, x);
	if (ret != NULL)
	{
		return ret;
	}
	return NULL;
}
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		//printf("NULL  ");
		return;
	}
	printf("%c  ", root->_data);
	BinaryTreePrevOrder(root->_left);
	BinaryTreePrevOrder(root->_right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		//printf("NULL  ");
		return;
	}
	BinaryTreeInOrder(root->_left);
	printf("%c  ", root->_data);
	BinaryTreeInOrder(root->_right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		//printf("NULL  ");
		return;
	}
	BinaryTreePostOrder(root->_left);
	BinaryTreePostOrder(root->_right);
	printf("%c  ", root->_data);
}
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode *front = QueueFront(&q);
		QueuePop(&q);
		printf("%c  ", front->_data);
		if (front->_left)
		{
			QueuePush(&q, front->_left);
		}
		if (front->_right)
		{
			QueuePush(&q, front->_right);
		}
	}
}
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode *front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)
		{
			break;
		}
		printf("%s ", front->_data);
		if (front->_left)
		{
			QueuePush(&q, front->_left);
		}
		if (front->_right)
		{
			QueuePush(&q, front->_right);
		}
	}
	while (!QueueEmpty(&q))
	{
		BTNode *front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			return 0;
		}
	}
	return 1;

}

还有最后一个树——线索二叉树
它的出现还是为了简约成本，实际上想一下算法和数据结构存在就是为了节约时间或空间，这个是节约不用的空指针域，
空的左孩子指针指向该结点的前驱,空的右孩子指针指向该结点的后继。这种附加的指针值称为线索，带线索的二叉树称为线索二叉树。

#include <stdio.h>  
#include <stdlib.h>  
#include <malloc.h>  
#define MAXSIZE 100  
typedef char ElemType;  
typedef enum  
{  
    Link,/*指向孩子结点*/Thread/*指向前驱或后继*/  
} PointerTag;  
typedef struct Node  
{  
    ElemType data;  
    struct Node *lchild;  
    struct Node *rchild;  
    PointerTag ltag,rtag;  
}*BitThrTree,BitThrNode;  
  
BitThrTree pre;  
void CreateBitTree2(BitThrTree *T,char str[]);//创建搜索二叉树  
void InThreading(BitThrTree p);//中序线索化二叉树  
int InOrderThreading(BitThrTree *Thrt,BitThrTree T);//通过中序遍历二叉树T，使T中序线索化。Thrt是指向头结点的指针  
int InOrderTraverse(BitThrTree T,int (*visit)(BitThrTree e));//中序遍历线索二叉树  
int Print(BitThrTree T);//打印二叉树的结点和线索标志  
BitThrNode* FindPoint(BitThrTree T,ElemType e);//在线索二叉树中查找结点为e的指针  
BitThrNode* InOrderPre(BitThrNode *p);//中序前驱  
BitThrNode* InOrderPost(BitThrNode *p);//中序后继  
void DestroyBitTree(BitThrTree *T);//销毁二叉树  
 
 
#include "LinkBiTree.h"  
  
void CreateBitTree2(BitThrTree *T,char str[])//创建搜索二叉树  
{  
    char ch;  
    BitThrTree stack[MAXSIZE];  
    int top = -1;  
    int flag,k;  
    BitThrNode *p;  
    *T = NULL,k = 0;  
    ch = str[k];  
    while(ch != '\0')  
    {  
        switch(ch)  
        {  
        case '(':  
            stack[++top] = p;  
            flag = 1;  
            break;  
        case ')':  
            top--;  
            break;  
        case ',':  
            flag = 2;  
            break;  
        default:  
            p = (BitThrTree)malloc(sizeof(BitThrNode));  
            p->data = ch;  
            p->lchild = NULL;  
            p->rchild = NULL;  
            if(*T == NULL)  
            {  
                *T = p;  
            }  
            else  
            {  
                switch(flag)  
                {  
                case 1:  
                    stack[top]->lchild = p;  
                    break;  
                case 2:  
                    stack[top]->rchild = p;  
                    break;  
                }  
                if(stack[top]->lchild)  
                {  
                    stack[top]->ltag = Link;  
                }  
                if(stack[top]->rchild)  
                {  
                    stack[top]->rtag = Link;  
                }  
            }  
        }  
        ch = str[++k];  
    }  
}  
void InThreading(BitThrTree p)//中序线索化二叉树  
{  
    if(p)//左子树线索化  
    {  
        InThreading(p->lchild);  
        if(!p->lchild)//前驱线索化  
        {  
            p->ltag = Thread;  
            p->lchild = pre;  
        }  
        if(!pre->rchild)//后继线索化  
        {  
            pre->rtag = Thread;  
            pre->rchild = p;  
        }  
        pre = p;  
        InThreading(p->rchild);//右子树线索化  
    }  
}  
int InOrderThreading(BitThrTree *Thrt,BitThrTree T)//通过中序遍历二叉树T，使T中序线索化。Thrt是指向头结点的指针  
{  
    if(!(*Thrt = (BitThrTree)malloc(sizeof(BitThrNode))))  
    {  
        exit(-1);//为头结点分配单元  
    }  
    (*Thrt)->ltag = Link;//修改前驱线索标志  
    (*Thrt)->rtag = Thread;//修改后继线索标志  
    (*Thrt)->rchild = *Thrt;//将头结点的rchild指针指向自己  
    if(!T)//如果二叉树为空，则将lchild指针指向自己  
    {  
        (*Thrt)->lchild = *Thrt;  
    }  
    else  
    {  
        (*Thrt)->lchild = T;//将头结点的左指针指向根结点  
        pre = *Thrt;//将pre指向已经线索化的结点  
        InThreading(T);//中序遍历进行中序线索化  
        /*将最后一个结点线索化*/  
        pre->rchild = *Thrt;//将最后一个结点的右指针指向头结点  
        pre->rtag  = Thread;//修改最后一个结点的rtag标志域  
        (*Thrt)->rchild = pre;//将头结点的rchild指针指向最后一个结点  
    }  
    return 1;  
}  
int InOrderTraverse(BitThrTree T,int (*visit)(BitThrTree e))//中序遍历线索二叉树  
{  
    BitThrTree p;  
    p = T->lchild ;//p指向根结点  
    while(p != T)//空树或遍历结束时，p == T  
    {  
        while(p->ltag == Link)  
        {  
            p = p->lchild ;  
        }  
        if(!visit(p))//打印  
        {  
            return 0;  
        }  
        while(p->rtag == Thread && p->rchild != T)//访问后继结点  
        {  
            p = p->rchild ;  
            visit(p);  
        }  
        p = p->rchild ;  
    }  
    return 1;  
}  
int Print(BitThrTree T)//打印二叉树的结点和线索标志  
{  
    static int k = 1;  
    printf("%2d\t%s\t %2c\t %s\t\n",k++,T->ltag == 0 ? "Link":"Thread",T->data ,T->rtag == 1 ? "Thread":"Link");  
    return 1;  
}  
BitThrNode* FindPoint(BitThrTree T,ElemType e)//在线索二叉树中查找结点为e的指针  
{  
    BitThrTree p;  
    p = T->lchild ;  
    while(p != T)  
    {  
        while(p->ltag == Link)  
        {  
            p = p->lchild ;  
        }  
        if(p->data == e)  
        {  
            return p;  
        }  
        while(p->rtag == Thread && p->rchild != T)  
        {  
            p = p->rchild ;  
            if(p->data == e)  
            {  
                return p;  
            }  
        }  
        p = p->rchild ;  
    }  
    return NULL;  
}  
BitThrNode* InOrderPre(BitThrNode *p)//中序前驱  
{  
    if(p->ltag == Thread)//如果p的标志域ltag为线索，则p的左子树结点为前驱  
    {  
        return p->lchild ;  
    }  
    else  
    {  
        pre = p->lchild ;//查找p的左孩子的最右下端结点  
        while(pre->rtag == Link)//右子树非空时，沿右链往下查找  
        {  
            pre = pre->rchild ;  
        }  
        return pre;//pre就是最右下端结点  
    }  
}  
BitThrNode* InOrderPost(BitThrNode *p)//中序后继  
{  
    if(p->rtag == Thread)//如果p的标志域rtag为线索，则p的右子树结点为后驱  
    {  
        return p->rchild ;  
    }  
    else  
    {  
        pre = p->rchild ;//查找p的右孩子的最左下端结点  
        while(pre->ltag == Link)//左子树非空时，沿左链往下查找  
        {  
            pre = pre->lchild ;  
        }  
        return pre;//pre就是最左下端结点  
    }  
}  
void DestroyBitTree(BitThrTree *T)//销毁二叉树  
{  
    if(*T)  
    {  
        if(!(*T)->lchild)  
        {  
            DestroyBitTree(&((*T)->lchild));  
        }  
        if(!(*T)->rchild)  
        {  
            DestroyBitTree(&((*T)->rchild));  
        }  
        free(*T);  
        *T = NULL;  
    }  
}  
 
 
#include "LinkBiTree.h"  
  
int main(void)  
{  
    BitThrTree T,Thrt;  
    BitThrNode *p,*pre,*post;  
    CreateBitTree2(&T,"(A(B(,D(G)),C(E(,H),F)))");  
    printf("线索二叉树的输出序列：\n");  
    InOrderThreading(&Thrt,T);  
    printf("序列  前驱标志  结点  后继标志\n");  
    InOrderTraverse(Thrt,Print);  
    p = FindPoint(Thrt,'D');  
    pre = InOrderPre(p);  
    printf("元素D的中序直接前驱元素是：%c\n",pre->data);  
    post = InOrderPost(p);  
    printf("元素D的中序直接后驱元素是：%c\n",post->data);  
    p = FindPoint(Thrt,'E');  
    pre = InOrderPre(p);  
    printf("元素E的中序直接前驱元素是：%c\n",pre->data);  
    post = InOrderPost(p);  
    printf("元素E的中序直接后驱元素是：%c\n",post->data);  
    DestroyBitTree(&Thrt);  
    return 0;  
}

哈夫曼树

到这数据结构算过去一半了，我们先来总结一下

点赞
收藏
关注作者

0/1000

抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认取消

加入云驻计划，成为创作者

华为云周边好礼
免费体验产品
特殊身份标识
线下官方门票
内部专家零距离
与10000+优质创作者共同成长

立即加入

码神爆肝数据结构——总长5w字，附带例题（下）

树

树的基本操作

双亲表示法

孩子表示法

孩子兄弟表示法

二叉树

顺序存储

链表存储

遍历二叉树

哈夫曼树

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

码神爆肝数据结构——总长5w字，附带例题（下）

树

树的基本操作

双亲表示法

孩子表示法

孩子兄弟表示法

二叉树

顺序存储

链表存储

遍历二叉树

哈夫曼树

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

推荐阅读

相关产品