- 微信
- 微博
  
  分享文章到微博
- 复制链接
  
  复制链接到剪贴板

相交链表 | 环形链表

跳动的bit 发表于 2022/04/27 07:13:58 2022/04/27

【摘要】 3.相交链表＜难度系数⭐＞📝 题述：给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null。(保证整个链式结构中不存在环且函数返回结果后，链表必须保持其原始结构。)⚠ 注意，其一，以下这种结构实际并不存在，因为3和1可以同时指向4，但4不能同时指向5和6。其二，这里比较的是节点的地址，不是节点的值💨 示例1：输...

3.相交链表＜难度系数⭐＞

📝 题述：给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null。(保证整个链式结构中不存在环且函数返回结果后，链表必须保持其原始结构。)

⚠ 注意，其一，以下这种结构实际并不存在，因为3和1可以同时指向4，但4不能同时指向5和6。其二，这里比较的是节点的地址，不是节点的值

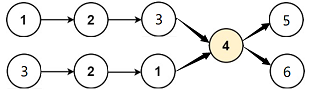
💨 示例1：
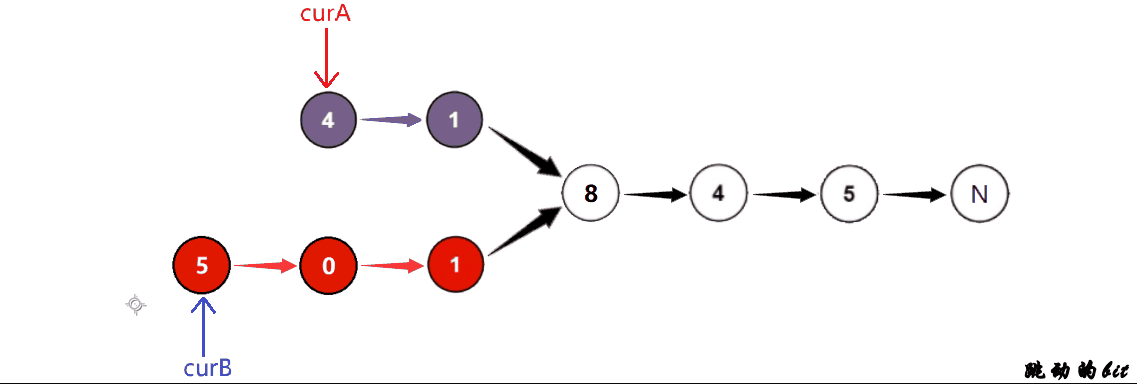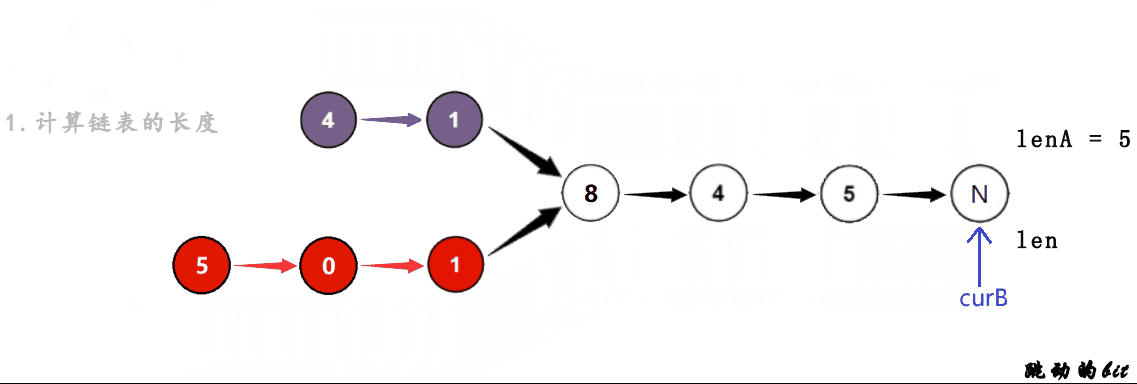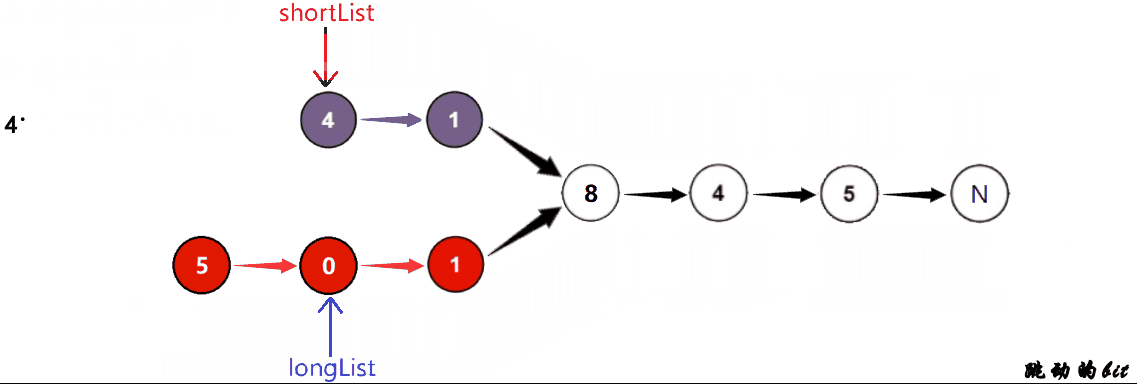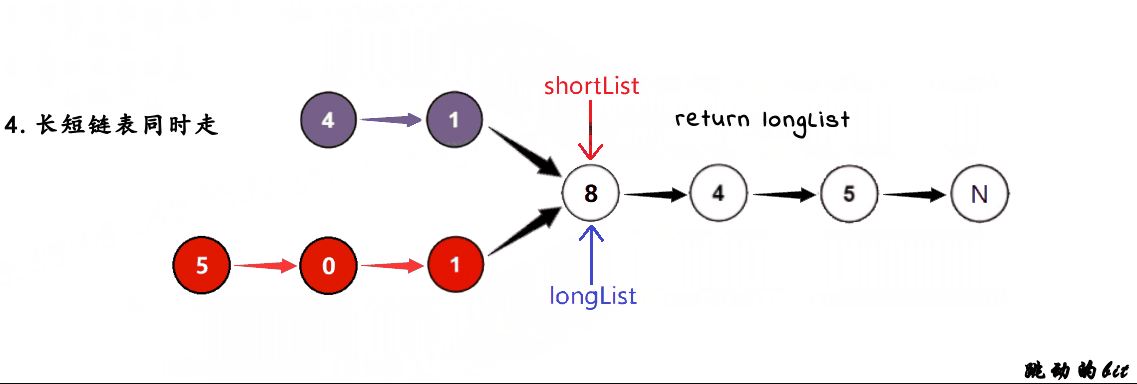
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at ‘8’

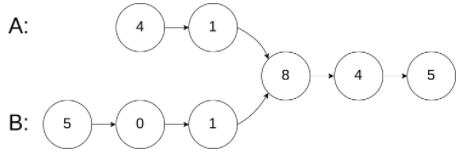
💨 示例2：
输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at ‘2’

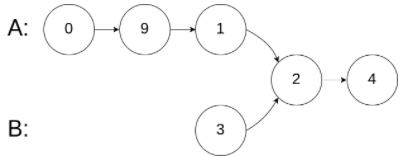
💨 示例3：
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null

🧷 平台：Visual studio 2017 && windows

🔑 核心思想：
常规暴力求解，A链表的每个节点和B链表的每个节点比较，如果有相同的就是交点，如果没有就不相交 (注意是节点的地址)，时间复杂度O(N^2)
对常规的方法进行优化：分别算出A和B的长度 lenA、lenB，让长的链表先走|lenA-lenB|，再同时走找交点，时间复杂度O(N)

leetcode原题

#include<stdio.h>
#include<stdlib.h>

typedef int SLTDataType;

struct ListNode
{
	int val;
	struct ListNode *next;
};

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
    struct ListNode* curA = headA;
    struct ListNode* curB = headB;
    int lenA = 0, lenB = 0;
    //计算链表的长度
    while(curA)
    {
        lenA++;
        curA = curA->next;
    }
    while(curB)
    {
        lenB++;
        curB = curB->next;
    }
    //先假设A长B短
    struct ListNode* longList = headA;
    struct ListNode* shortList = headB;
    //如果假设错了，就交换下
    if(lenA < lenB)
    {
        longList = headB;
        shortList = headA;
    }
    //让长的走差距步
    int gap = abs(lenA-lenB);
    while(gap--)
    {
        longList = longList->next;
    }
    //长的和短的同时走
    while(longList && shortList)
    {
        //找到了，相交
        if(longList == shortList)
        {
            return longList;
        }
        //没找到继续走
        longList = longList->next;
        shortList = shortList->next;
    }
    //没找到，不相交
    return NULL;
}
int main()
{
	struct ListNode* n1 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n1->val = 4;

	struct ListNode* n2 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n2->val = 1;

	struct ListNode* m1 = (struct ListNode*)malloc(sizeof(struct ListNode));
	m1->val = 5;

	struct ListNode* m2 = (struct ListNode*)malloc(sizeof(struct ListNode));
	m2->val = 0;
	
	struct ListNode* m3 = (struct ListNode*)malloc(sizeof(struct ListNode));
	m3->val = 1;

	struct ListNode* u1 = (struct ListNode*)malloc(sizeof(struct ListNode));
	u1->val = 8;

	struct ListNode* u2 = (struct ListNode*)malloc(sizeof(struct ListNode));
	u2->val = 4;
	
	struct ListNode* u3 = (struct ListNode*)malloc(sizeof(struct ListNode));
	u3->val = 5;
	//上节点
	n1->next = n2;
	n2->next = u1;
	u1->next = u2;
	u2->next = u3;
	u3->next = NULL;
	//下节点
	m1->next = m2;
	m2->next = m3;
	m3->next = u1;
	u1->next = u2;
	u2->next = u3;
	u3->next = NULL;
	
	getIntersectionNode(n1, m1);
	return 0;
}

4.环形链表＜难度系数⭐＞

📝 题述：给定一个链表，判断链表中是否有环。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。如果链表中存在环，则返回 true 。否则，返回 false 。

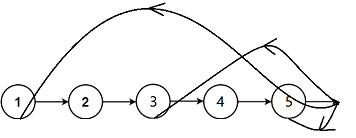
带环链表不能轻易的去遍历，否则会死循环

💨 示例1：
输入：head = [3,2,0,-4], pos = 1
输出：true

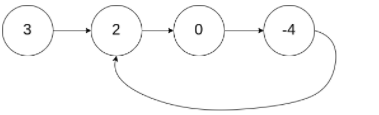
💨 示例2：
输入：head = [1,2], pos = 0
输出：true

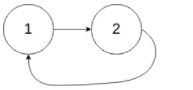
💨 示例3：
输入：head = [1], pos = -1
输出：false

🧷 平台：Visual studio 2017 && windows

🔑 核心思想：
快慢指针，如果快指针和慢指针相遇了就是带环的，否则快指针指向空时就是不带环的

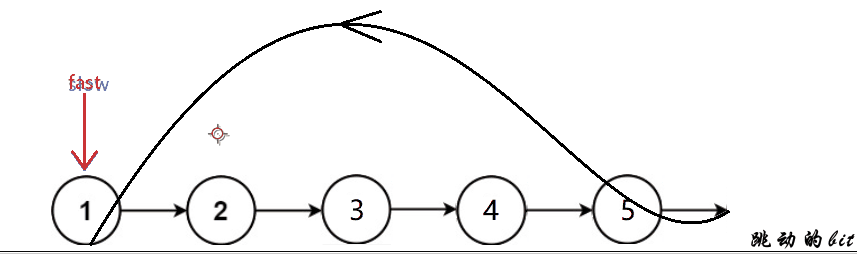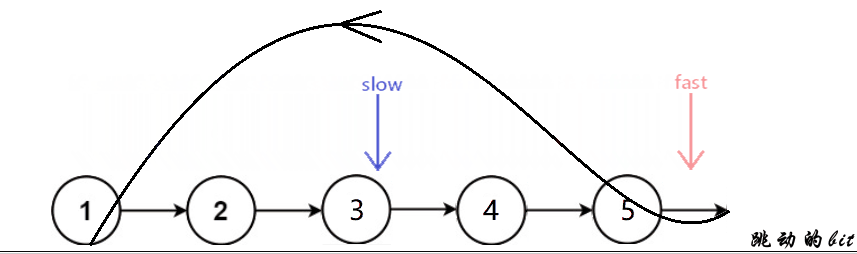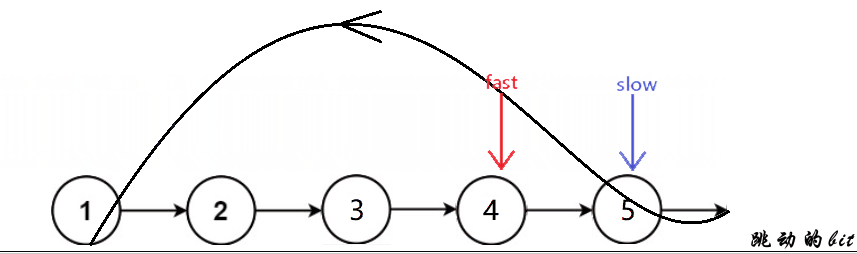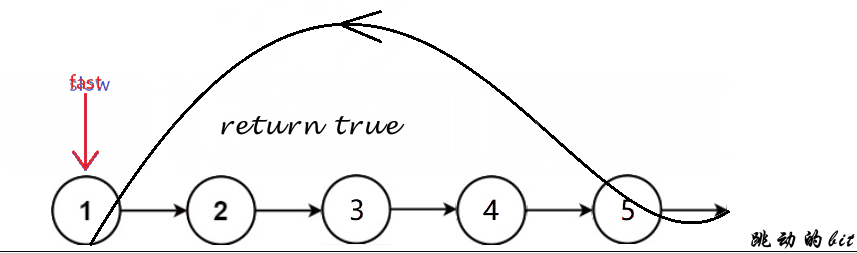
leetcode原题

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>


typedef int SLTDataType;

struct ListNode
{
	int val;
	struct ListNode *next;
};
bool hasCycle(struct ListNode* head) 
{
    struct ListNode *slow = head, *fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        //相遇即带环
        if(slow == fast)
        {
            return true;
        }
    }
    //不带环
    return false;
}
int main()
{
	struct ListNode* n1 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n1->val = 1;

	struct ListNode* n2 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n2->val = 2;

	struct ListNode* n3 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n3->val = 3;

	struct ListNode* n4 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n4->val = 4;
	
	struct ListNode* n5 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n5->val = 5;

	n1->next = n2;
	n2->next = n3;
	n3->next = n4;
	n4->next = n5;
	n5->next = n3;
	
	hasCycle(n1);
	return 0;
}

其实这道题并不难，相对较难的是这道题的延伸：

🧿 slow一次走一步，fast一次走两步，fast一定可以相遇slow吗？请证明

slow一次走一步，fast一次走两步时，它们一定可以相遇
slow进环时，fast已经在环里走一会了，那么这时在环内就产生了fast追赶slow的现象。假设环的长度是C、slow进环时，fast和slow之间的距离是N，那么进环后fast和slow之间的距离变化是：
N
N-1
N-2
…
2
1
0
slow和fast之间的距离是0的时候就能相遇，同时也说明了N为奇或偶时都能相遇
最简单的理解就是：fast每次都以一步的距离追赶slow，slow走一步，fast走二步可以等同于slow不走，fast走一步，

🧿 slow一次走一步，fast一次走n步(n > 2,3,4,5…)，fast一定可以相遇slow吗？请证明

slow一次走一步，fast一次走n步时，它们不一定可以相遇
假设slow一次走1步，fast一次走3步，假设环的长度是C、slow进环时，fast和slow之间的距离是N。那么进环后fast和slow之间的距离变化是：
偶   奇
N    N
N-2 N-2
N-4 N-4
…    …
2 1
0 -1 -1相当于它们的距离变成了C-1
slow和fast之间的距离是0的时候就能相遇，同时说明N是偶数时，就一定能相遇(假设N是奇数，且C-1也是奇数，就永远不能相遇)
最简单的理解就是：fast每次都以2步的距离追赶slow，slow走一步，fast走三步可以等同于slow不走，fast走二步，

💨 总结
fast一次走x步，slow一次走y步都是可以的，但最重要的是追赶过程中的步差x-y。步差是1，一定能追上；步差不是1，不一定能追上

5.环形链表＜难度系数⭐⭐＞

📝 题述：给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。说明：不允许修改给定的链表。进阶：使用 O(1) 空间解决此题

💨 示例1：
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点

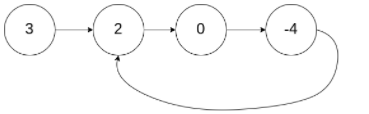
💨 示例2：
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点

💨 示例3：
输入：head = [1], pos = -1
输出：返回 null

🧷 平台：Visual studio 2017 && windows

🔑 核心思想：
思路一，一个指针从相遇点走，另一个指针从head走，它们会在入口点相遇(待证)

思路二，把相遇点的位置断开，这时就变成了相交问题(调用之前实现的相交函数)

leetcode原题

#include<stdio.h>
#include<stdlib.h>

typedef int SLTDataType;

struct ListNode
{
	int val;
	struct ListNode *next;
};
//思路一
struct ListNode* detectCycle1(struct ListNode *head)
{
    struct ListNode *slow = head, *fast = head;
    //结束条件：无环，快指针走到空了；有环，返回入环的节点
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        //相遇了
        if(slow == fast)
        {
            //记录相遇的节点
            struct ListNode* meet = slow;
            //头节点和相遇点同时走，它们会在入口点相遇，也就是说在入口点时，头节点和相遇点是相同的
            while(head != meet)
            {
                head = head->next;
                meet = meet->next;
            }
            //有环，返回相遇节点
            return meet;
        }
    }
    //无环，返回空
    return NULL;
}
//思路二
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
	    struct ListNode* curA = headA;
    struct ListNode* curB = headB;
    int lenA = 0, lenB = 0;
    //计算链表的长度
    while(curA)
    {
        lenA++;
        curA = curA->next;
    }
    while(curB)
    {
        lenB++;
        curB = curB->next;
    }
    //先假设A长B短
    struct ListNode* longList = headA;
    struct ListNode* shortList = headB;
    //如果假设错了，就交换下
    if(lenA < lenB)
    {
        longList = headB;
        shortList = headA;
    }
    //让长的走差距步
    int gap = abs(lenA-lenB);
    while(gap--)
    {
        longList = longList->next;
    }
    //长的和短的同时走
    while(longList && shortList)
    {
        //找到了，相交
        if(longList == shortList)
        {
            return longList;
        }
        //没找到继续走
        longList = longList->next;
        shortList = shortList->next;
    }
    //没找到，不相交
    return NULL;
}
struct ListNode* detectCycle2(struct ListNode *head)
{
   struct ListNode *slow, *fast;
   slow = fast = head;
   while(fast && fast->next)
   {
       slow = slow->next;
       fast = fast->next->next;

       //带环相遇点
       if(slow == fast)
       {
           //断开
           struct ListNode* meet = slow;
           struct ListNode* next = meet->next;
           meet->next = NULL;
           return getIntersectionNode(head, next);
       }
   }
   return NULL;
}
int main()
{
	struct ListNode* n1 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n1->val = 1;

	struct ListNode* n2 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n2->val = 2;

	struct ListNode* n3 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n3->val = 3;

	struct ListNode* n4 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n4->val = 4;
	
	struct ListNode* n5 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n5->val = 5;

	n1->next = n2;
	n2->next = n3;
	n3->next = n4;
	n4->next = n5;
	n5->next = n3;
	
	detectCycle1(n1);
	detectCycle2(n1);
	return 0;
}

🧿 证明：一个指针从相遇点走，另一个指针从head走，它们会在入口点相遇
假设链表头到入口点的距离是L，假设相遇点到入口点的距离是X，假设环的长度是C。
错误推论：当快慢指针相遇时，慢指针走的长度是L+X，快指针走的长度是L+C+X，由此就可以推出2(L+X) = L+C+X，再推出L+X=C，L= C-X。看似没毛病，但实际这个推导是错的，因为slow进环前，fast不一定在环里只走一圈

正确推论：慢指针走的长度是L+X，快指针走的长度是L+N * C+X (N表示圈数&&N>=1)。由此就可以推出2(L+X) = L+N * C+X ，再推出L+X=N*C，L=N * C-X，可分解为L=(N-1) * C+C-X，(N-1) * C表示从相遇点走了N-1圈，C-X表示相遇点到入口的距离。最后通过这个公式就可以推出一个指针从链表头走，一个指针从相遇点走，会在入口点相遇。

点赞
收藏
关注作者

0/1000

抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认取消

加入云驻计划，成为创作者

华为云周边好礼
免费体验产品
特殊身份标识
线下官方门票
内部专家零距离
与10000+优质创作者共同成长

立即加入

相交链表 | 环形链表

3.相交链表＜难度系数⭐＞

4.环形链表＜难度系数⭐＞

5.环形链表＜难度系数⭐⭐＞

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

相交链表 | 环形链表

3.相交链表＜难度系数⭐＞

4.环形链表＜难度系数⭐＞

5.环形链表＜难度系数⭐⭐＞

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

推荐阅读

相关产品