目录
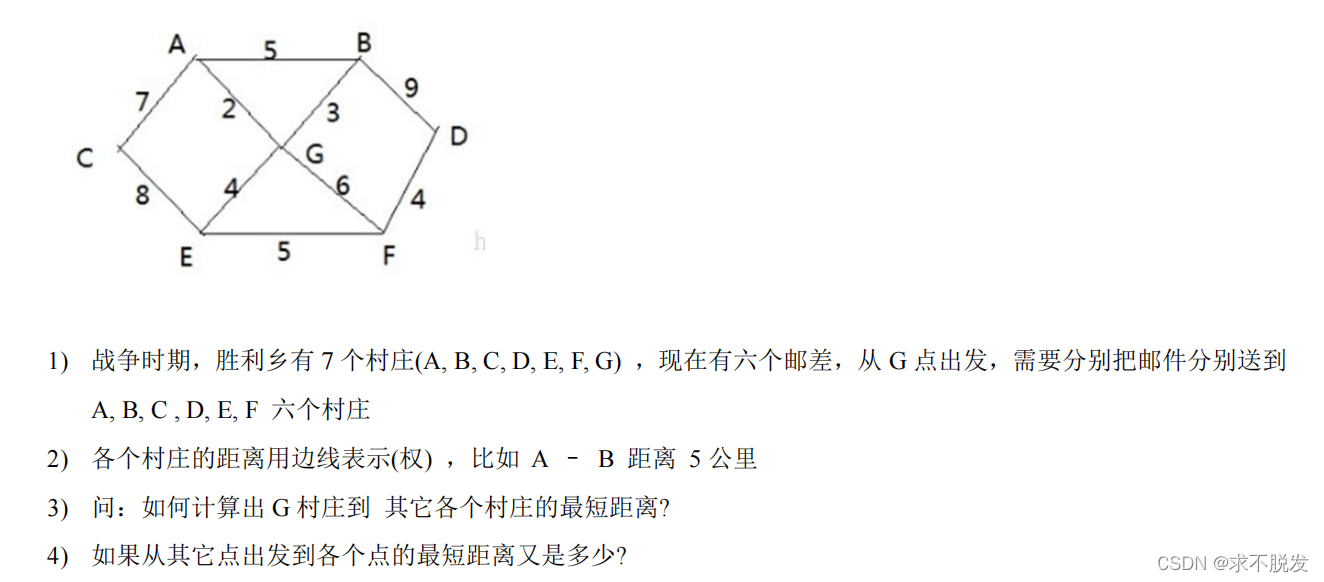
算法介绍
应用实例
算法步骤
代码实现
算法介绍
迪杰斯特拉( Dijkstra )算法是典型最短路径算法,用于计算一个结点到其他结点的最短路径。它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
应用实例


算法步骤
1)设置出发顶点为 v ,顶点集合 VfvI ,v2, vi .), v 到 V 各顶点的距离构成距离集合 Dis , Dis ( dI ,d2, di .), Dis 集合记录着 v 到图中各顶点的距离(到自身可以看作0, v 到 vi 距离对应为 di )
2)从 Dis 中选择值最小的 di 并移出 Dis 集合,同时移出 V 集合中对应的项点 vi ,此时的 v 到 vi 即为最短路径
3)更新 Dis 集合,更新规则为:比较 v 到 V 集合中顶点的距离值,与 v 通过 vi 到 V 集合中顶点的距离值,保留
值较小的一个(同时也应该更新顶点的前驱节点为 vi ,表明是通过 vi 到达的)
4)重复执行两步骤,直到最短路径顶点为目标顶点即可结束。
代码实现
import java.util.Arrays;
public class _最短路{
static int[] vis;//标记已经访问的顶点 0未访问 1 访问
static int[] dis;//出发顶点到各个下标对应顶点的最短距离
static int[] pre;//每个下标对应的上一个顶点下标
static char[] vertex;//顶点
static int[][] matrix;//邻接矩阵
public static void main(String[] args) {
vertex= new char[]{'A','B','C','D','E','F','G'};
matrix = new int[vertex.length][vertex.length];
chushihua(matrix);//初始化邻接矩阵
djstl(vertex.length,6);//调用算法
}
public static void djstl(int length,int start) {
vis=new int[length];
dis=new int[length];
pre=new int[length];
Arrays.fill(dis, 9999);//初始化距离为较大值
dis[start] = 0;//初始化出发顶点到自身的距离0
/* 先将起始点到与其连通的顶点的路径及pre前一个顶点进行更新*/
update(start);
//在以与起始点相连的顶点为起点 更新距离和路径
for (int i = 1; i < vertex.length; i++) {
int minIndex = -1;
int mindis=9999;
//找到一个最短路径
for (int j = 0; j < vertex.length; j++) {
if(vis[j]==0 && dis[j] < mindis) {
minIndex = j;
mindis = dis[j];
}
}
vis[minIndex] = 1;
update(minIndex);//继续更新
}
System.out.println(Arrays.toString(dis));
}
/**
* 以index顶点向下查找!!!以起点start到index附近的邻接结点的最短路径!!!
* @param index
*/
public static void update(int index) {
vis[index] = 1;//index标记为已访问
int len= 0;//len:从start顶点到index顶点的距离+上从index再到i顶点的距离
//循环遍历每个邻接结点顶点,找到真正意义上的最短路径
for (int i = 0; i < matrix[index].length; i++) {
//记录从start顶点到index顶点的距离+上从index再到i顶点的距离
len = dis[index] + matrix[index][i];
//将dis[i] 即从start直接到i 的距离 与len进行比较
if(vis[i] == 0 && len < dis[i]) {
dis[i] = len;//更新最短路径
pre[i] = index;//更新前置顶点
}
}
}
/**
* 初始化邻接矩阵
* @param matrix
*/
public static void chushihua(int[][] matrix) {
final int N = 9999;
matrix[0]=new int[]{N,5,7,N,N,N,2};
matrix[1]=new int[]{5,N,N,9,N,N,3};
matrix[2]=new int[]{7,N,N,N,8,N,N};
matrix[3]=new int[]{N,9,N,N,N,4,N};
matrix[4]=new int[]{N,N,8,N,N,5,4};
matrix[5]=new int[]{N,N,N,4,5,N,6};
matrix[6]=new int[]{2,3,N,N,4,6,N};
}
}

【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com


评论(0)