【蓝桥杯省赛】冲刺练习题【数学公式】倒计时【06】天(准考证组委会已下发,请查询)
🙏🤗距离【第十三届蓝桥杯4月9日省赛】仅剩【06天】🤗🙏
📋今日题型:【数学公式】📋
⭐️🤗循环是一切暴力的基础,暴力基础,转起来。🤗⭐️
🤗国一镇楼🤗
📋比赛题目与分数比例📋
确认范围:
结果填空题5道,共计45分。
程序设计题5道,共计105分。
⭐️🤗刷题安排🤗⭐️
| 日期 | 题目类型 | 题目数量 |
| 3月25日 | 循环 | 6 |
| 3月26日 | 超大数 | 6 |
| 3月27日 | 数组 | 6 |
| 3月28日 | 枚举 | 6 |
| 3月29日 | 递归 | 6 |
| 3月30日 | 绘图 | 6 |
| 3月31日 | 深搜广搜 | 5 |
| 4月1日 | 动态规划 | 5 |
| 4月2日 | 填空题 | 5 |
| 4月3日 | 数学公式:查询准考证
|
5 |
| 4月4日 | 第十届省赛题 | 10 |
| 4月5日 | 第十一届省赛题 | 10 |
| 4月6日 | 第十二届省赛1套题 | 10 |
| 4月7日 | 第十二届省赛2套题 | 10 |
| 4月8日 | 经典题目练习 | 8 |
| 4月9日 | 9点考试 |
目录
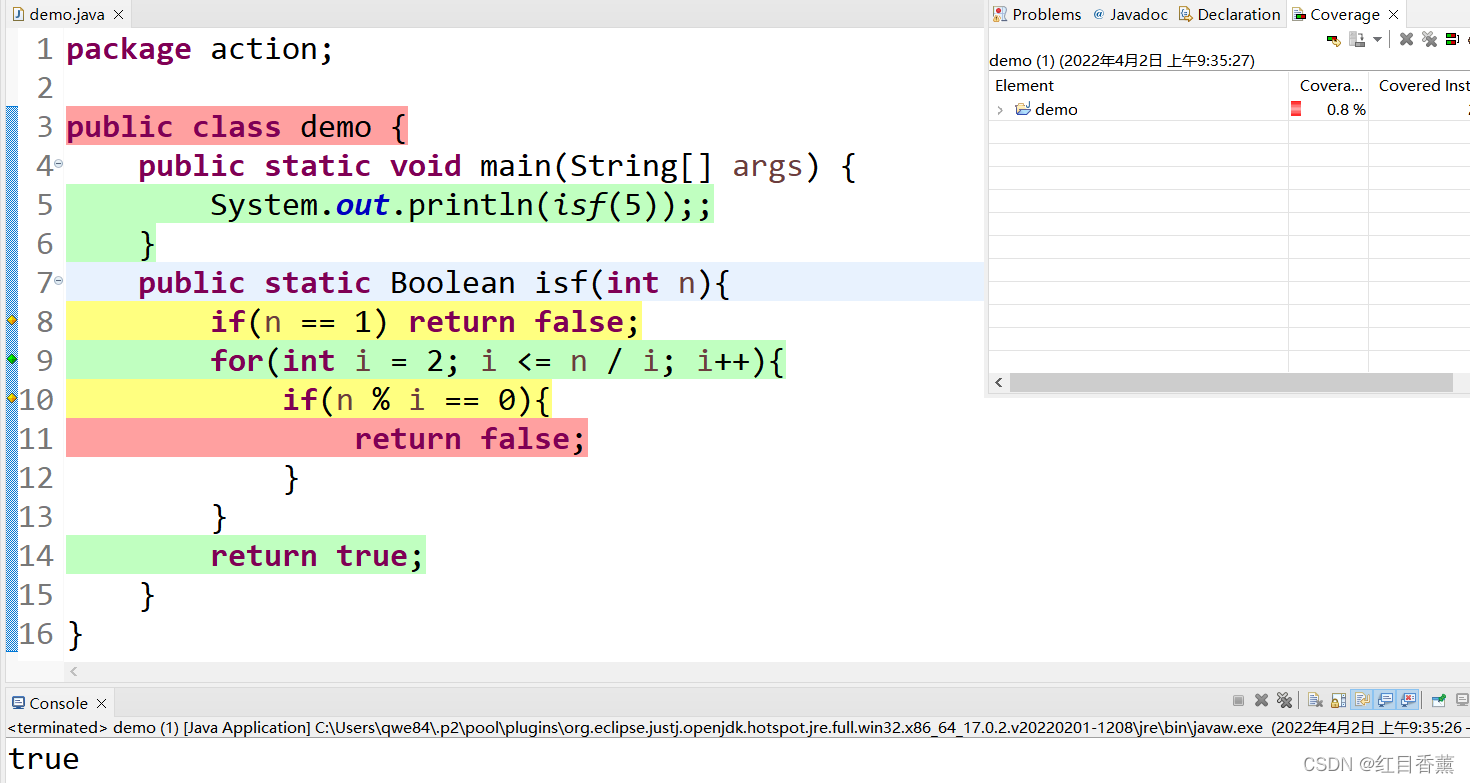
1、判断质数
质数又称为素数,是指大于1的并且除了1和它本身外,没有其他因数的自然数。
判断一个数是否是质数
假设该数为n, 我们只需要判断内是否有n的因子。如果有,则n为合数,否则,n为质数。
这种方法被称为试除法, 即试着除一下所有可能的因子。
2、分解质因数
根据算术基本定理又称唯一分解定理,对于任何一个合数, 我们都可以用几个质数的幂的乘积来表示。
接下来我们利用这个公式分解质因数。
设一个质数为p.如果n%p == 0,那么p就是n的一个质因数,接下来就是求p的指数,我们让n = n/p, 这样就从n中剔除了一个p,接着重复上述两步,直到n%p != 0
3、快速幂
当我们计算时,常用的做法是对n连乘k次, 但如果k特别大,假如k = 1e6, 如果仍然对n连乘1e6次的话,时间消耗就太大了。那么我们如何在短时间内求出一个数的k次方呢。
求
快速幂
没有处理超大数
3、欧几里得定力
最大公约数、最小公倍数
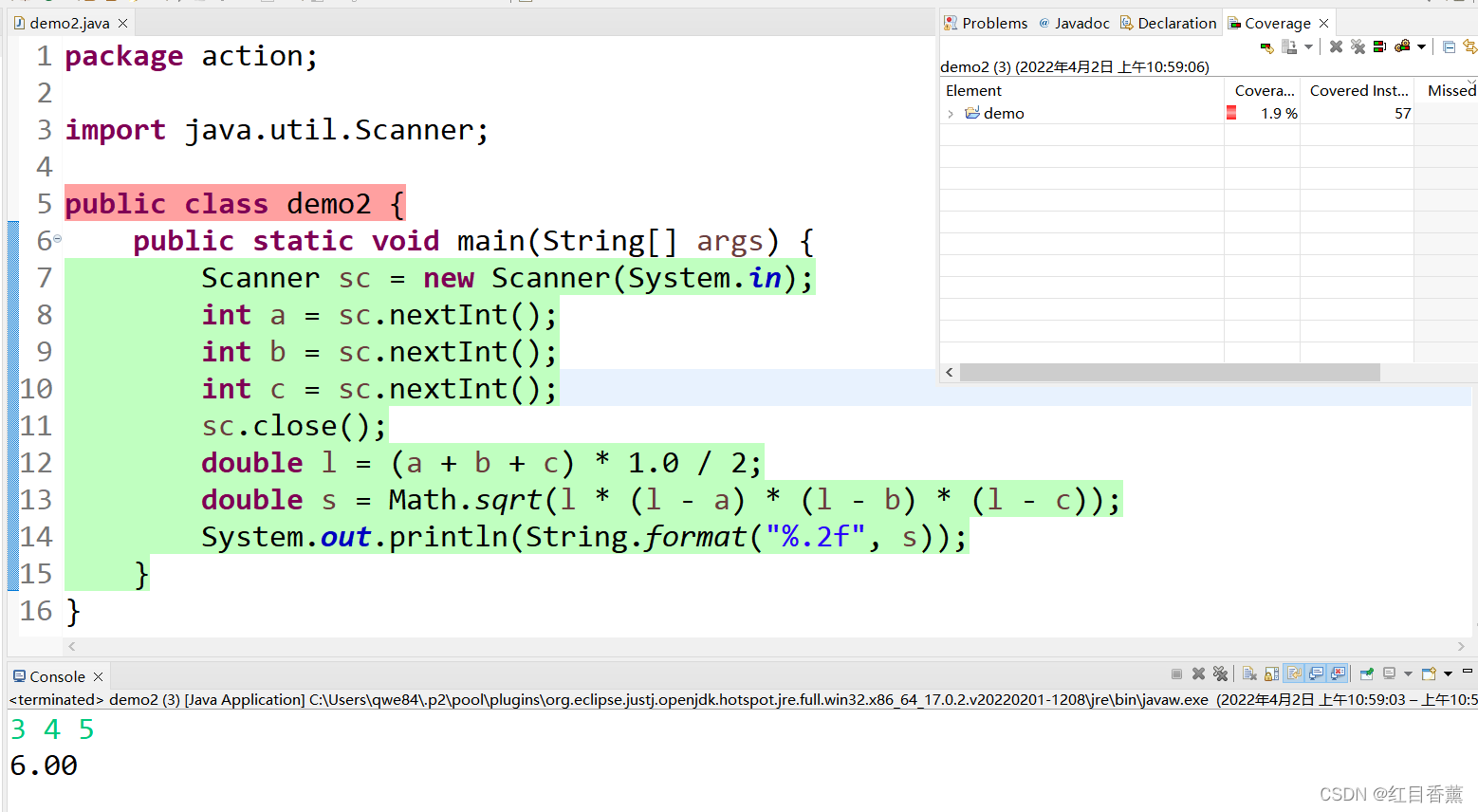
4、海伦公式(求三角形面积)
5、排列数公式
排列数公式就是从n个不同元素中,任取m(m≤n)个元素(被取出的元素各不相同),按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。排列与元素的顺序有关,组合与顺序无关。加法原理和乘法原理是排列和组合的基础。
排列数:
从n个不同的元素中任取m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m(m≤n)个元素的排列数。记作符号 。A是英文arrangement(排列)的第一个大写字母。
例如,从7个不同的元素中任取5个元素的排列数为 ,从10个不同的元素中任取7个元素的排列数为。
排列数公式
公式A是排列公式,从N个元素取M个进行排列(即排序)。
符号
C:组合数
A:排列数(在旧教材为P)
N:元素的总个数
M:参与选择的元素个数
!:阶乘,如5!=5×4×3×2×1=120
C:Combination 组合
P:Permutation排列 (现在教材为A-Arrangement)
推导过程
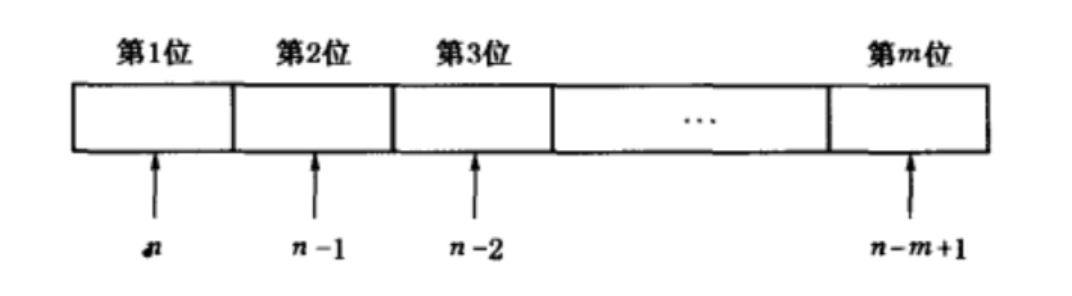
求排列数可以按依次填m个空位来考虑:假定有排好顺序的m个空位,从n个不同元素a1,a2,a3,…,an中任意取m个去填空,一个空位填1个元素,每一种填法就对应1个排列,因此,所有不同填法的种数就是排列数。
填空可分为m个步骤:
第1步,第1位可以从n个元素中任选一个填上,共有n种填法;
第2步,第2位只能从余下的n-1个元素中任选一个填上,共有n-1种填法;
第3步,第3位只能从余下的n-2个元素中任选一个填上,共有n-2种填法;
……
第m步,当前面的m-1个空位都填上后,第m位只能从余下的n-(m-1)个元素中任选一个填上,共有n-m+1种填法。
根据分步计数原理,全部填满m个空位共有n(n-1)(n-2)…(n-m+1)种填法。所以得到公式:
这里n,m∈N*,并且m≤n这个公式叫做排列数公式其中,公式右边第一个因数是n,后面的每个因数都比它前面一个因数少1,最后个因数为n-m+1,共有m个因数相乘。
排列数公式还可以写成:
注意:为了保证公式在n=m时成立,特规定0! =1。
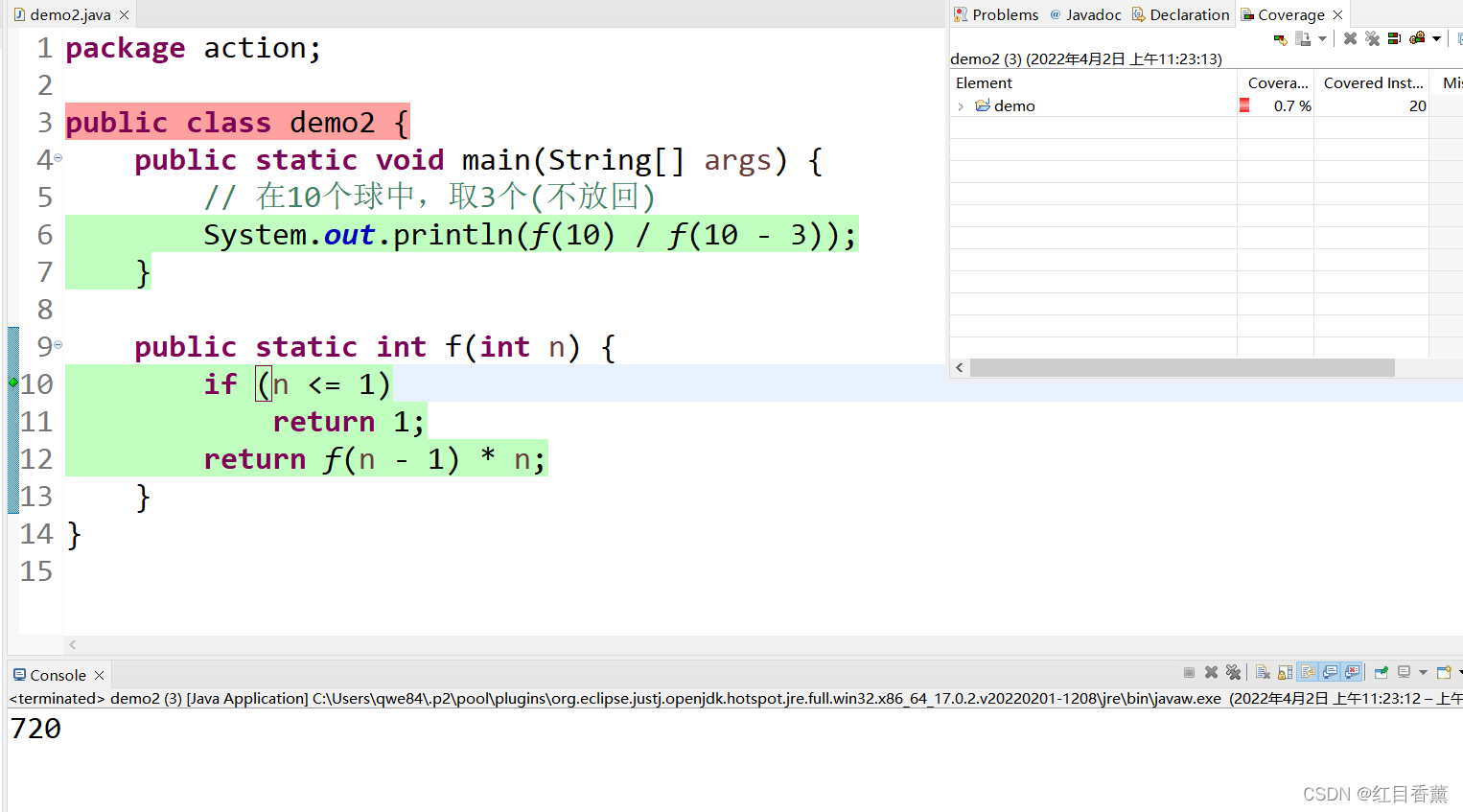
示例:
在10个球中,任意取3个(不放回),求有多少种取法?
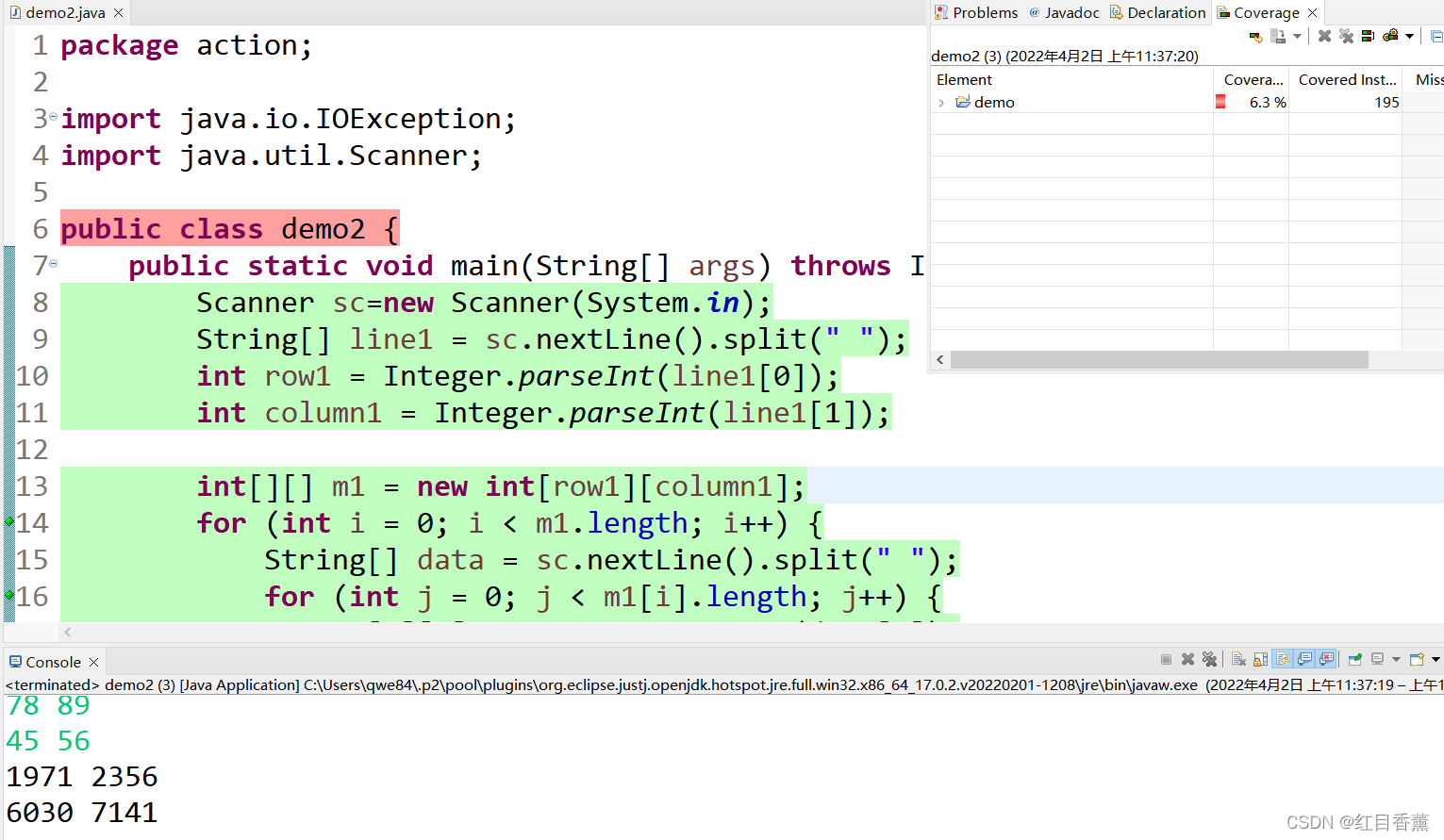
附加1:矩阵相乘
资源限制
内存限制:256.0MB C/C++时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s
问题描述
小明最近在为线性代数而头疼,线性代数确实很抽象(也很无聊),可惜他的老师正在讲这矩阵乘法这一段内容。
当然,小明上课打瞌睡也没问题,但线性代数的习题可是很可怕的。
小明希望你来帮他完成这个任务。
现在给你一个ai行aj列的矩阵和一个bi行bj列的矩阵,
要你求出他们相乘的积(当然也是矩阵)。
(输入数据保证aj=bi,不需要判断)
输入格式
输入文件共有ai+bi+2行,并且输入的所有数为整数(long long范围内)。
第1行:ai 和 aj
第2~ai+2行:矩阵a的所有元素
第ai+3行:bi 和 bj
第ai+3~ai+bi+3行:矩阵b的所有元素
输出格式
输出矩阵a和矩阵b的积(矩阵c)
(ai行bj列)
样例输入
样例输出
附加2:线性同余方程(B组以上)
数论中,线性同余方程是最基本的同余方程,“线性”表示方程的未知数次数是一次.
在数论中,线性同余方程是最基本的同余方程,“线性”表示方程的未知数次数是一次,即形如:
ax≡b (mod n)的方程。
此方程有解当且仅当 b 能够被 a 与 n 的最大公约数整除(记作 gcd(a,n) | b)。
这时,如果 x0 是方程的一个解,那么所有的解可以表示为:
其中 d 是a 与 n 的最大公约数。在模 n 的完全剩余系 {0,1,…,n-1} 中,恰有 d 个解。
理论示例:
在方程3x ≡ 2 (mod 6)中, d = gcd(3,6) = 3 ,3 不整除 2,因此方程无解。
在方程5x ≡ 2 (mod 6)中, d = gcd(5,6) = 1,1 整除 2,因此方程在{0,1,2,3,4,5} 中恰有一个解: x=4。
在方程4x ≡ 2 (mod 6)中, d = gcd(4,6) = 2,2 整除 2,因此方程在{0,1,2,3,4,5} 中恰有两个解: x=2 and x=5。
代码示例:
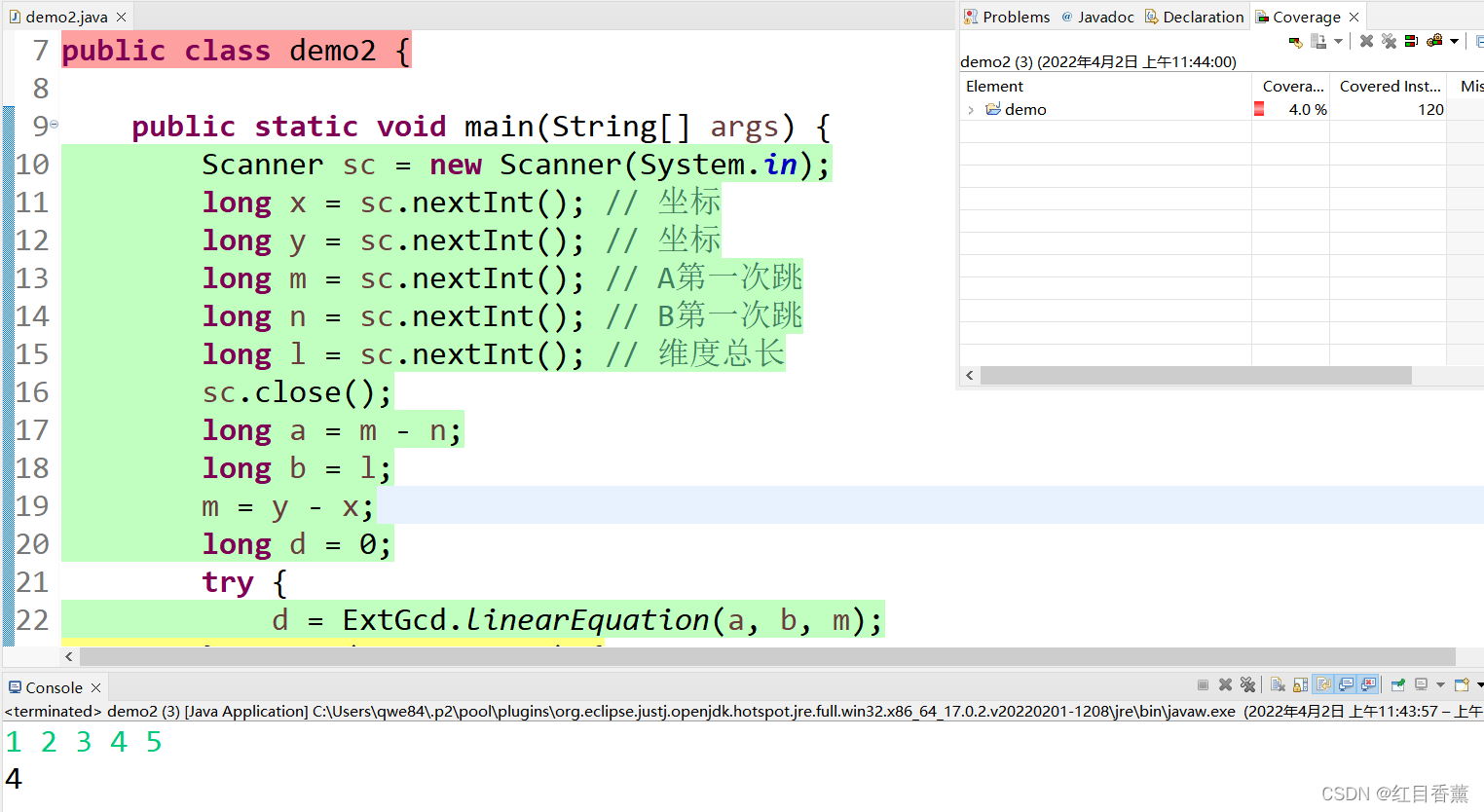
青蛙的约会
两只青蛙在网上相识了,它们聊得很开心,于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上,于是它们约定各自朝西跳,直到碰面为止。可是它们出发之前忘记了一件很重要的事情,既没有问清楚对方的特征,也没有约定见面的具体位置。不过青蛙们都是很乐观的,它们觉得只要一直朝着某个方向跳下去,总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上,不然是永远都不可能碰面的。为了帮助这两只乐观的青蛙,你被要求写一个程序来判断这两只青蛙是否能够碰面,会在什么时候碰面。
我们把这两只青蛙分别叫做青蛙A和青蛙B,并且规定纬度线上东经0度处为原点,由东往西为正方向,单位长度1米,这样我们就得到了一条首尾相接的数轴。设青蛙A的出发点坐标是x,青蛙B的出发点坐标是y。青蛙A一次能跳m米,青蛙B一次能跳n米,两只青蛙跳一次所花费的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。
输入
输入只包括一行5个整数x,y,m,n,L,
其中x≠y < 2000000000,0 < m、n < 2000000000,0 < L < 2100000000。
输出
输出碰面所需要的跳跃次数,如果永远不可能碰面则输出一行"Impossible"
输入示例
输出示例
题目分析
设跳次数为t,则跳t次后两个青蛙的位置分别为(x+mt) mod L、(y+nt) mod L,相遇即是(x+mt)%L=(y+nt)%L转化为ax+by=c方程: (m-n)t+kL=y-x。设a=m-n,b=L,c=y-x,然后套用拓展欧几里得即可得出答案。
- 点赞
- 收藏
- 关注作者




![[2, \sqrt{n} ]](https://res-hd.hc-cdn.cn/ecology/9.3.204/v2_resources/ydcomm/libs/images/loading.gif)
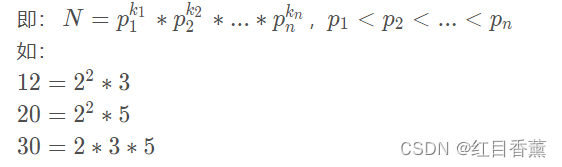



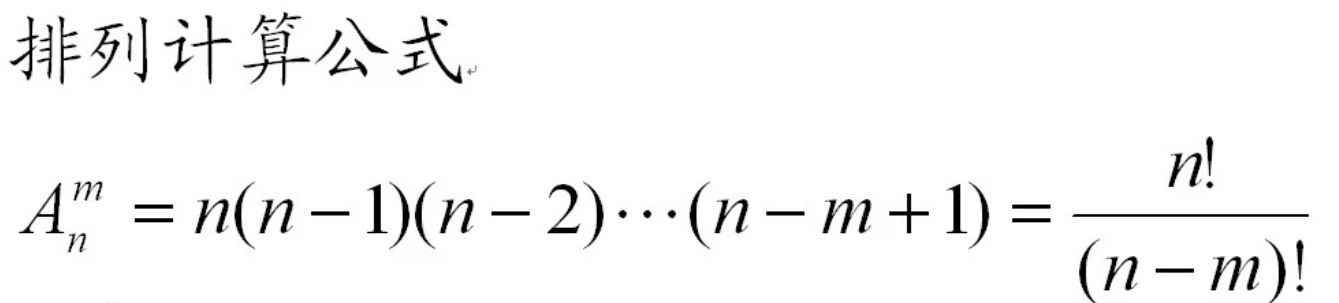
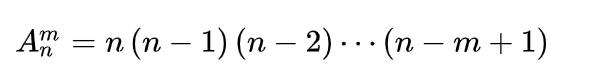
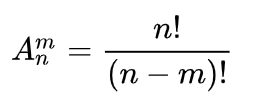

评论(0)