累积分布函数和直方图哪个更好？

我们的大多数统计评估都依赖于累积分布函数 (CDF)。尽管直方图乍一看似乎更直观并且需要较少的解释，但实际上 CDF 提供了几个优点，值得熟悉它。CDF 的主要优点以及我们主要使用它而不是直方图的原因在对两个图的主要解释之后列出如下。

基本说明

在探讨不同地块的优势之前，首先在此对其进行描述。

应该给出一组数字。这些可以来自任何类型的测量、模拟或任意其他数据源。只是为了说明，我们刚刚使用 MATLAB 随机数生成器生成了一些正态分布的数字：

x=randn(100,1)*10+50

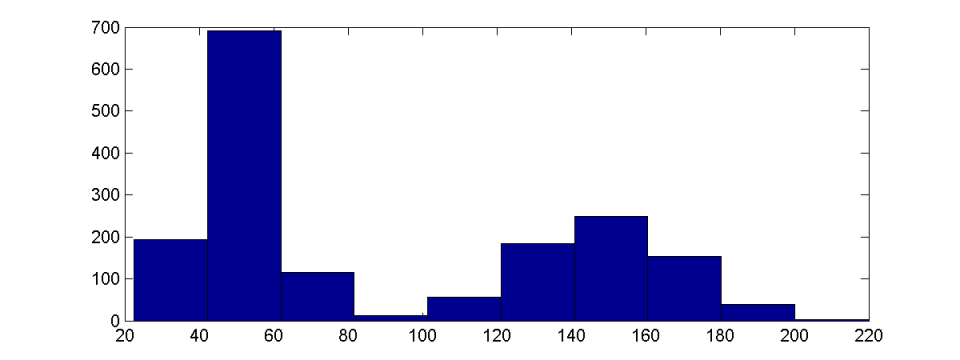
在直方图的帮助下显示这些数字，数字的结果范围被分成一定数量的均匀间隔 - 所谓的bins。然后将每个 bin 内数字的绝对或相对计数绘制为相应间隔的条形图。上一个示例的结果可能如下图所示：

另一方面，在累积分布函数 (CDF) 中，已排序数字的百分比或相对计数绘制在数字本身上。这或多或少是直方图的积分。

前面的示例数字导致下图：

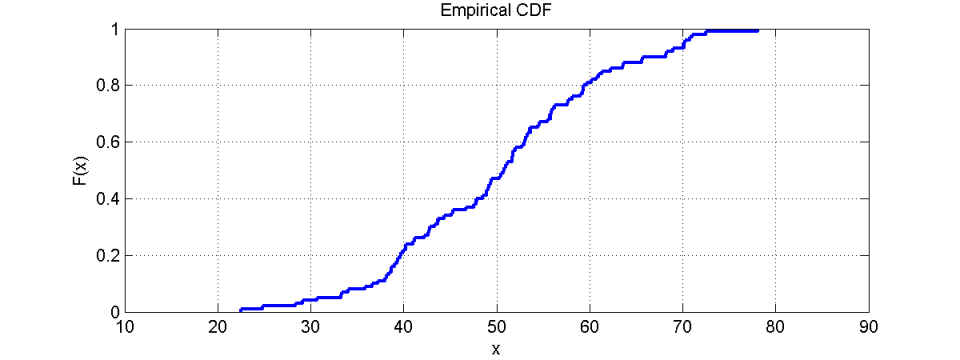
该图意味着来自给定数字集的F(x)值的相对数量小于或等于值x。

在我们看来，这张图有很多本质的优势。

基本关键值的直接定量读取

CDF 相对于直方图的主要优势之一是可以直接从图表中读取主要和重要的关键值和特征，如最小值、最大值、中值、分位数、百分位数等。

可以在 CDF 开始并碰到 x 轴的点处看到最小值。在 CDF 到达线y=1并结束的地方可以看到最大值。百分位数和分位数也可以直接从x轴读取。

给定数字集中的每个值都是 CDF 中的某个点。在我们的一些 CDF 评估中，我们实现了在 CDF 中单击该点时直接命名该点或其值。在直方图中，无法单独处理数字样本。

异常值检测

在某些情况下，使用直方图检测异常值可能会出现问题。作为示例，我们将值 400 添加到上面的给定示例数字中。相应的直方图如下所示：

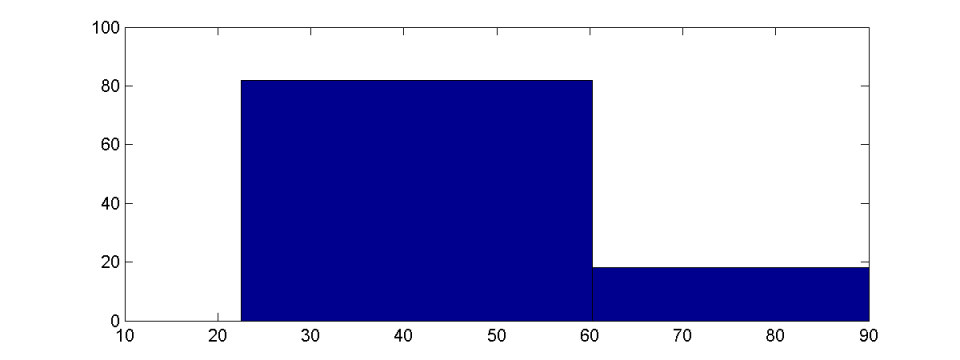
如果数据集很大，由于与值总数的关系相对较小，可能无法很好地看到异常值。另一方面，异常值以原始分布可能变得难以识别的方式扩展了 bin 的大小。因此，必须根据离群值到主要值的距离来扩展 bin 的数量。但这通常只能在事后很好地完成，而不是先验的，或者需要一些复杂的算法来选择 bin 大小。如果 x 轴的限制没有根据异常值而改变，则异常值也可能完全被监督。直方图没有表明在显示的轴限制之外仍然存在数据。

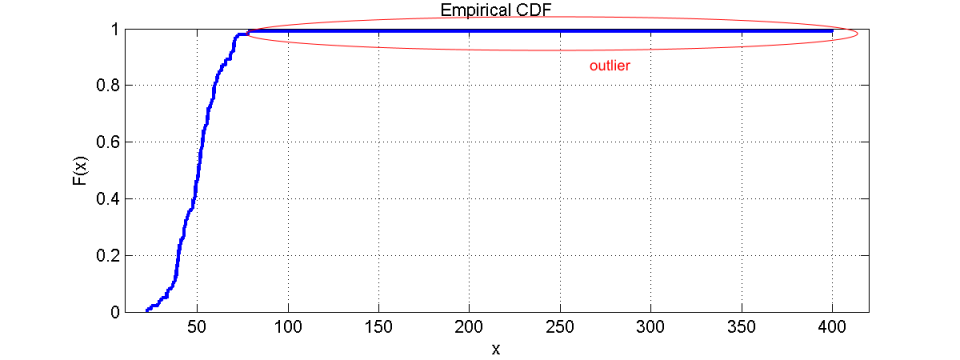
在累积分布函数内，可以通过 CDF 曲线的尾部看到异常值。它们的值在尾部的末端直接可见。此外，即使由于异常值导致x 轴重新缩放，分布类型也保持可见。

如果不更改x轴的限制以容纳所有数据，由于分布函数并未在轴限制之前结束且未到达y=1线，因此异常值的存在仍然很明显.

无穷大值的显示

如果某些无穷大值是数据集的一部分，则在直方图中根本看不到它们的存在。在 CDF 中，可以看到无穷大值的存在，因为绘图没有到达下线y=0（对于-Inf）或上线y=1（对于+Inf）。CDF 末端到上下线的距离也表示无穷大值的相对数量。对于负无穷大和正无穷大都是如此。有时我们用圆圈标记这些值，以突出和容易识别这些值。

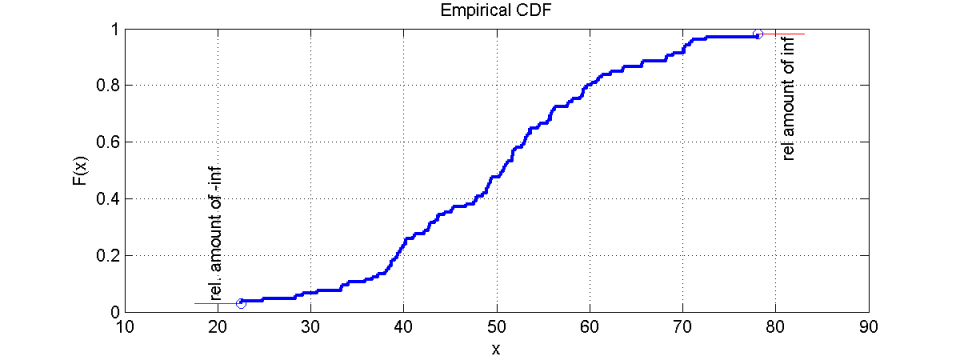
分配类型的识别

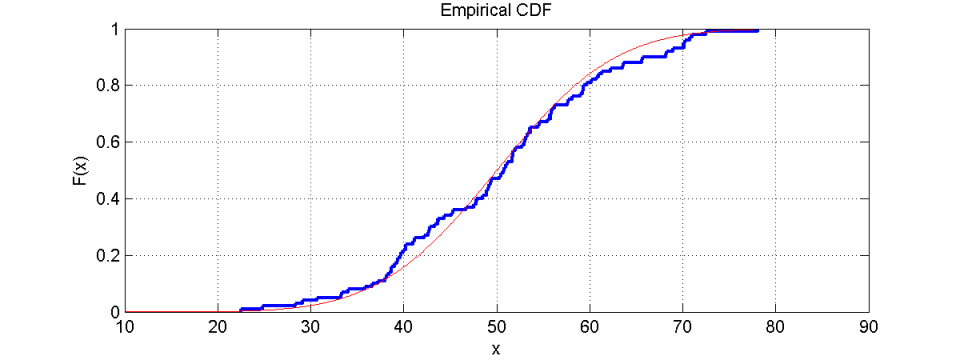
我们同意使用直方图可以更简单地识别分布类型。在直方图中，人们可以轻松识别数据是正态分布还是遵循任何不同的分布类型。另一方面，如果不仅绘制了经验分布函数本身，还绘制了预期分布类型的 CDF（比较下图中正态分布的红线），则可以直接应用 Kolmogorov Smirnov 检验。这两条曲线在 y 方向的最大距离验证了分布的类型。这种差异越小，关于分布类型的证据就越多。

集群的识别

与分布类型一样，在直方图中可以很容易地看到集群的存在。

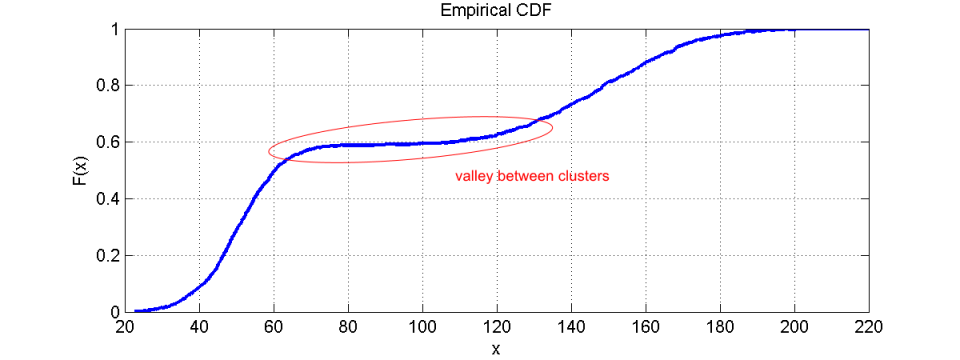
但是只需很少的部分，也可以在 CDF 中清楚地看到集群。一个人只需要寻找下降的斜率，之后梯度会再次增加。下图中可以看到一个示例，它依赖于与上面的直方图相同的数字。

几个数据集的比较

CDF 比直方图更适合比较多个数据集。可以将任意数量的 CDF 绘制到相同的轴上，而不会出现任何比较问题。因此，每个集合实际包含多少数据无关紧要。

直方图很快就会变得混乱，并且很难在视觉上区分不同的数据集。除了直方图的所有其他缺点之外，在此处生成这些缺点也更加复杂。例如，所有数据集的所有 bin 都必须同步。这甚至可能恶化直方图的现有缺点。

防止误解和操纵的安全性

直方图的另一个缺点是它对某些显示参数（如 bin 大小）的敏感性。以下面的正态分布数据集为例，该数据集已由 MATLAB 随机数生成器 ( randn(20,1))再次生成：

[0.5377, 0.5377, 1.8339, -2.2588, 0.8622, 0.3188, -1.3077, -0.4336, 0.3426, 3.5784, 2.7694, -1.3499, 3.0349, 0.7254, -0.063, 0.7147, -0.2050, -0.1241, 1.4897, 1.4090, 1.4172]

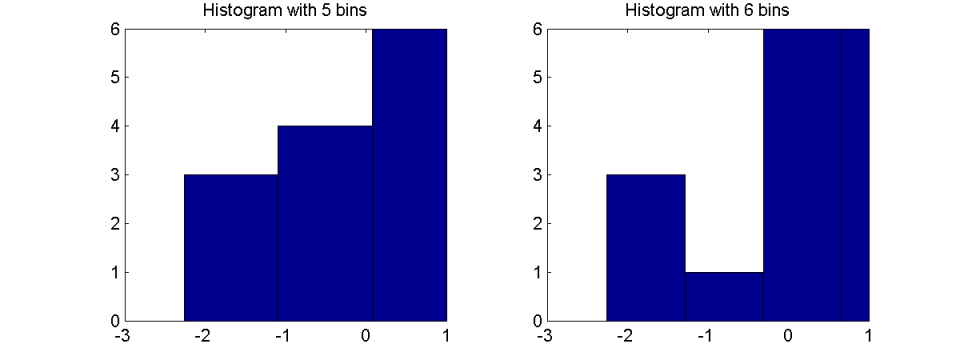
根据所选的 bin 数量，生成的图表可能会有很大差异：

具有 5 个 bin 的直方图与预期的正态分布在很大程度上相关。同样的数字看起来完全不同，当选择6个直方图条块进行说明的时候. 在这种情况下，直方图看起来像具有 3 个集群的多峰分布，而不是正态分布。

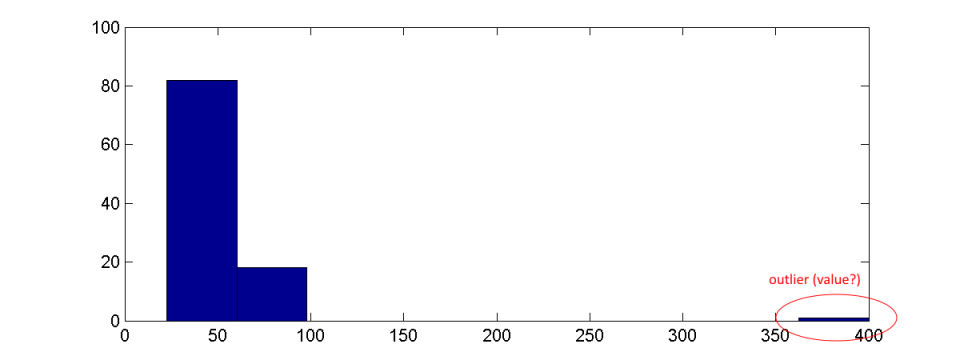
如果不巧选择了轴限制，画面会变得更糟：

与此相反，CDF 的显示始终清晰且独特。如果在数据集范围内定义了轴限制，则 CDF 不会到达线y=0或y=1。这清楚地表明还有一些在当前视图中看不到的可用数据。这样，CDF 对“操纵”和由于不吉利的显示参数造成的误解更加稳健。