1 RBF神经网络介绍

RBF（Radial Basis Function, RBF）网络和BP网络一样都是非线性多层前向网络，在任
何情况下可以互相代替。BP神经网络是一种全局逼近网络，学习速率相对慢些，不适合
实时性等要求较高的场合。而RBF网络被证明对非线性网络具有一致逼近性，可以逼近
任意的非线性函数，结构简单，并且具有很快的学习收敛速度。因此RBF网络有较为广
泛的应用
径向基网络是一种单隐层前馈神经网络，使用径向基函数作为隐层神经元的激活函数，
而输出层则是隐层输出的线性组合。径向基神经网络可分为正则化网络和广义网络，广
义RBF网络是由正则化网络稍加变化得到的，被应用的较多

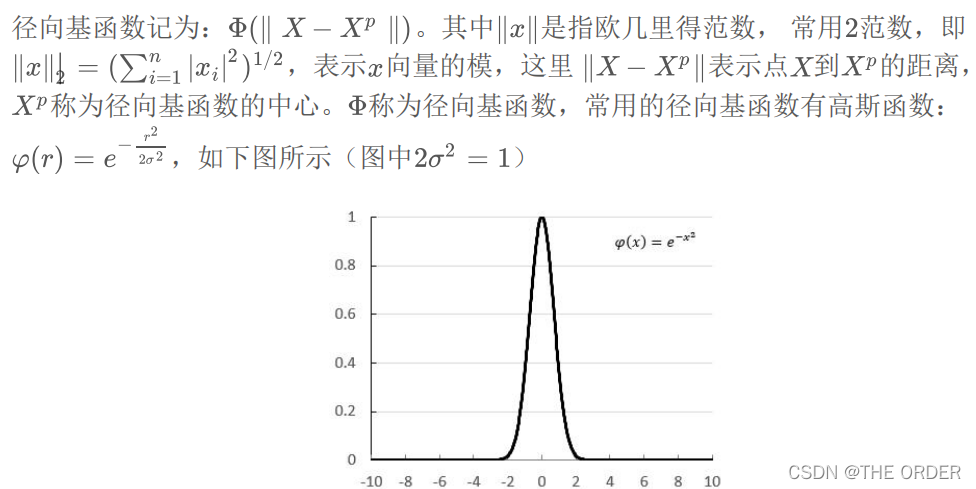
2 径向基函数

3 正则化网络

正则化网络中，所有的输入样本作为径向基函数的中心Xp，即这里隐层节点数等于输入
样本数P。各径向基函数选择统一的标准差σ，从隐层到输出层之间采用与权值向量
W加权和的形式进行线性组合

4 权值调整——目标输出

5 权值调整——算法

6 局限性和解决途径

正则化逼近性能依赖于足够多的训练样本，但是如果训练样本的样本量P过大，需要
计算P timesP 矩阵的逆，网络计算量将大的惊人（通用矩阵相乘算法的复杂度是
O(P 3)，优化算法的复杂度是O(P 2.807) ），从而导致过低的效率甚至根本不可能实
现。
· 另一个局限性是当一个矩阵很大时，它是病态矩阵的可能性就很高，也就是说Φ中的
一个微小扰动将对结果W产生很大影响。
· 这些问题的解决方案是减少隐层神经元的个数，使其阶跃输入维度数和样本量之间。
此时求得的解是较低维度空间上的次优解。

7 广义BPF网络

广义RBF网络是针对正则化网络的局限性稍加变化得到的，主要体现在径向基函数的
中心tj及基函数标准差的选取上，而且在隐层加入了阈值参数来与基函数共同求加权
和。广义RBF网络中隐节点的个数M远小于样本个数P，基函数的中心更多的由训练
算法确定。
· 根据径向基函数中心确定方法的不同，对应有不同的学习策略，常见的有：随机选取
固定中心；自组织选取中心；有监督选取中心。

8 例子说明

RBF主要是低位映射到高维，通过减去径向基中心生成高维数据
正则化RBF网络是选取所有X作为径向基中心，广义RBF是选择有限数据进行映射
$ $x_1 x_2$
$x^1$ 2 4
$x^2$ 1 1
$x^3$ 3 1
$x^4$ 2 2

分别以x1，x2，x3，x4为径向基中心点求距离，然后再映射后成为四维数据，变成线性可分
0 $\sqrt{\smash[b]{10}}$ $\sqrt{\smash[b]{10}}$ 2
$\sqrt{\smash[b]{10}}$ 0 2 $\sqrt{\smash[b]{2}}$
$\sqrt{\smash[b]{10}}$ 2 0 $\sqrt{\smash[b]{2}}$
2 $\sqrt{\smash[b]{2}}$ $\sqrt{\smash[b]{2}}$ 0

径向基函数生成新数据，x离中心约近y越大，越远y越小，新数据一定是线性可分的