主成成分分析（PCA)讲解与应用（一）

概念

存在一定的相关性,比如在研究上海世界博览会影响力评价时,就要考虑多个评价变量。当变量个数较多且变量之间存在复杂关系时,会显著增加分析问题的复杂性。如果有一种方法可以将多个变量综合为少数几个代表性变量,使这些变量既能够代表原始变量的绝大多数信息又互不相关,那么这样的方法无疑有助于对问题的分析和建模。这样的方法就是主成成分分析。

PCA步骤

1. 对原始数据进行标准化处理
2. 计算样本相关系数矩阵
3. 计算相关系数矩阵R的特征值和相应的特征向量
4. 选择重要的主成分,并写出主成分表达式
5. 计算主成分得分
6. 依据主成分得分的数据,进一步对问题进行后续的分析和建模

企业综合实力排序案例分析与matlab实现

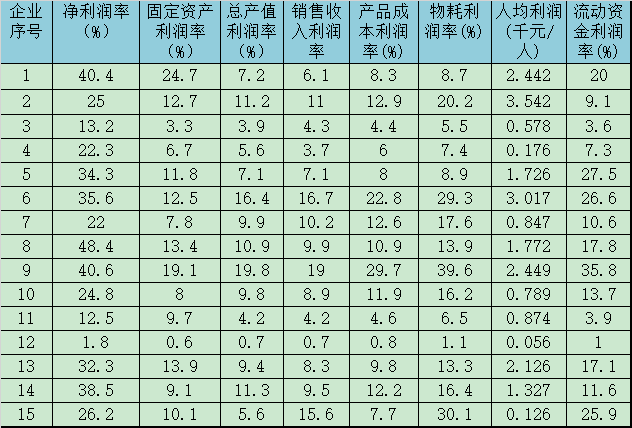
为了系统地分析某IT类企业的经济效益﹐选择了8个不同的利润指标,对15家企业进行了调研,并得到如下所示的数据。请根据这些数据对这15家企业进行综合实力排序。

matlab代码实现：

clear all
clc
%% 数据导入处理
clc
clear all
A = xlsread('t.xlsx'

文章来源: chuanchuan.blog.csdn.net，作者：川川菜鸟，版权归原作者所有，如需转载，请联系作者。

原文链接：chuanchuan.blog.csdn.net/article/details/122738208