2022美赛单变量深度学习LSTM 时间序列分析预测
【摘要】
换汤不换药,有手就会
基础肥皂案例
数据集如下: 你的数据只要能跟它合上就行,年份和数据。 你只需要修改的地方:
套上去就完事,完整代码:
# coding=gbk
"""
作者:川...
换汤不换药,有手就会
基础肥皂案例
数据集如下:
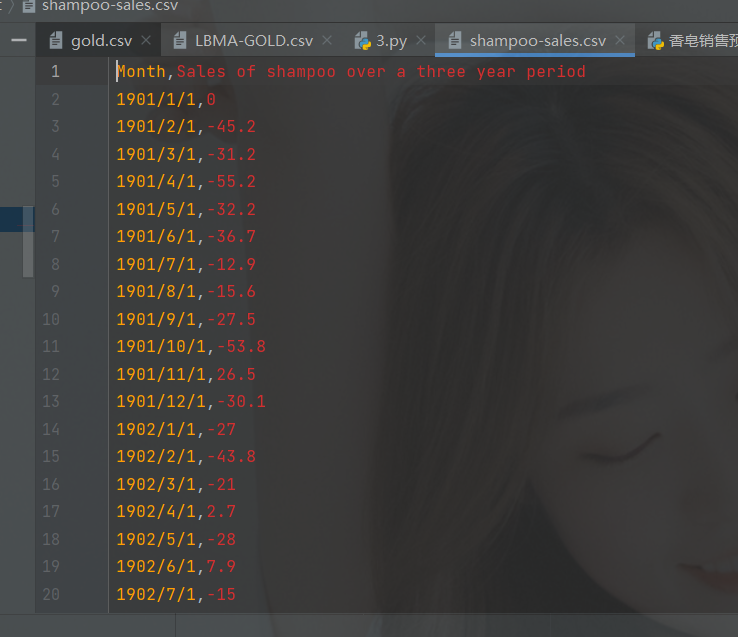
你的数据只要能跟它合上就行,年份和数据。
你只需要修改的地方:
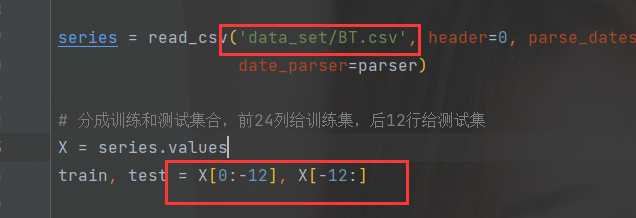
套上去就完事,完整代码:
# coding=gbk
"""
作者:川川
公众号:玩转大数据
@时间 : 2022/2/18 19:03
群:701163024
"""
from pandas import read_csv
from pandas import datetime
from sklearn.metrics import mean_squared_error
from math import sqrt
from matplotlib import pyplot
# 加载数据
def parser(x):
return datetime.strptime(x, '%Y/%m/%d') #年月日
series = read_csv('data_set/BT.csv', header=0, parse_dates=[0], index_col=0, squeeze=True,
date_parser=parser)
# 分成训练和测试集合,前24列给训练集,后12行给测试集
X = series.values
train, test = X[0:-12], X[-12:]
'''
步进验证模型:
其实相当于已经用train训练好了模型
之后每一次添加一个测试数据进来
1、训练模型
2、预测一次,并保存预测结构,用于之后的验证
3、加入的测试数据作为下一次迭代的训练数据
'''
#把数组train赋值给一个history列表
history = [x for x in train]
#创建一个predictions列表,这个列表记录了观测值,创建一个predictions数组中第n个元素,对应test数组中第n-1个元素
predictions = list()
for i in range(len(test)):
predictions.append(history[-1]) # history[-1],就是执行预测,这里我们只是假设predictions数组就是我们预测的结果
history.append(test[i]) # 将新的测试数据加入模型
# 预测效果评估
rmse = sqrt(mean_squared_error(test, predictions))#返回的结果是测试数组test,和观测数组predictions的标准差,https://www.cnblogs.com/nolonely/p/7009001.html
print('RMSE:%.3f' % rmse)
# 画出预测+观测值
pyplot.plot(test)#测试数组
pyplot.plot(predictions)#观测数组
pyplot.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
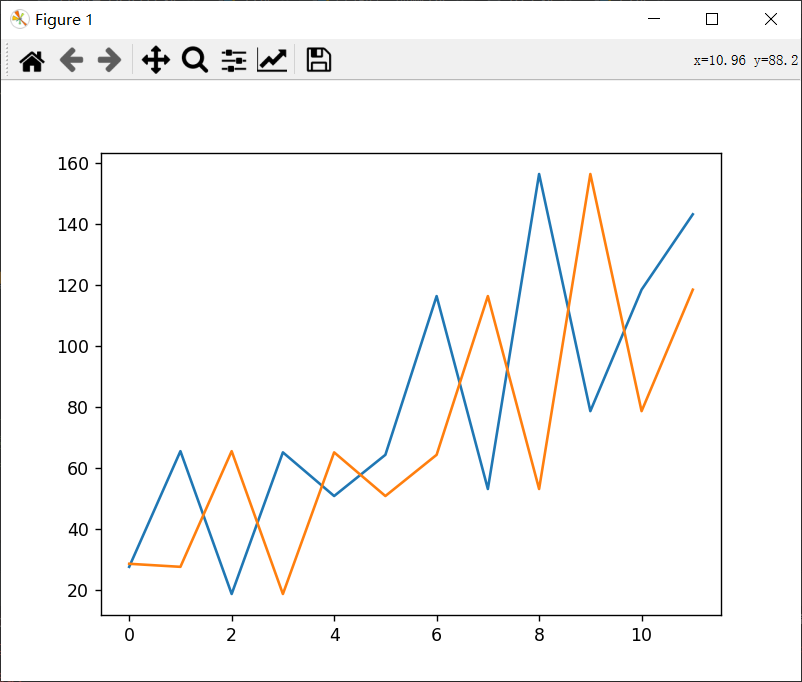
完整文件:
链接:https://pan.baidu.com/s/1FgDKr6ZF__OBuahkpy2PFg?pwd=dat5
提取码:dat5
--来自百度网盘超级会员V3的分享
- 1
- 2
- 3
升级版肥皂案例
数据还是如下:
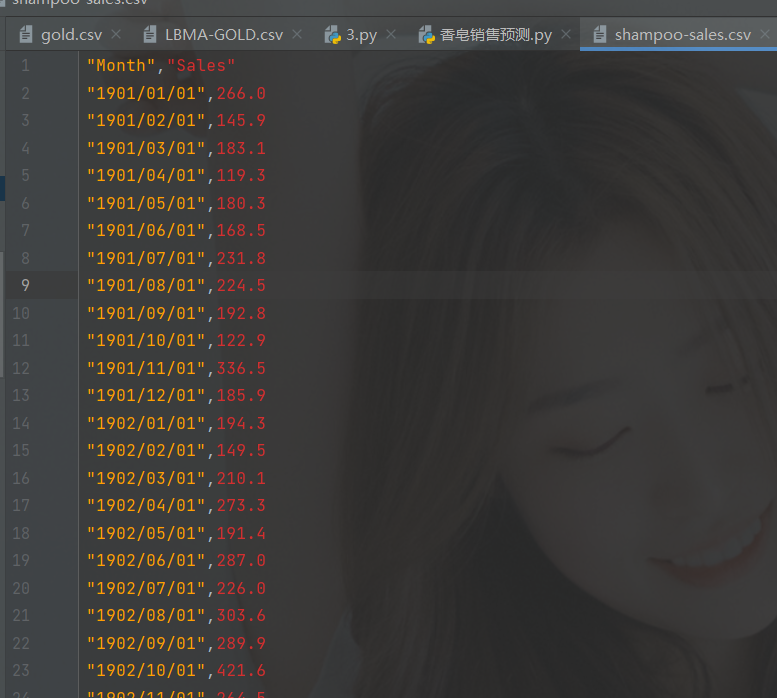
代码如下,你可以根据自己的数据集修改一下路径罢了:
# coding=utf-8
from pandas import read_csv
from pandas import datetime
from pandas import concat
from pandas import DataFrame
from pandas import Series
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from math import sqrt
from matplotlib import pyplot
import numpy
# 读取时间数据的格式化
def parser(x):
return datetime.strptime(x, '%Y/%m/%d')
# 转换成有监督数据
def timeseries_to_supervised(data, lag=1):
df = DataFrame(data)
columns = [df.shift(i) for i in range(1, lag + 1)] # 数据滑动一格,作为input,df原数据为output
columns.append(df)
df = concat(columns, axis=1)
df.fillna(0, inplace=True)
return df
# 转换成差分数据
def difference(dataset, interval=1):
diff = list()
for i in range(interval, len(dataset)):
value = dataset[i] - dataset[i - interval]
diff.append(value)
return Series(diff)
# 逆差分
def inverse_difference(history, yhat, interval=1): # 历史数据,预测数据,差分间隔
return yhat + history[-interval]
# 缩放
def scale(train, test):
# 根据训练数据建立缩放器
scaler = MinMaxScaler(feature_range=(-1, 1))
scaler = scaler.fit(train)
# 转换train data
train = train.reshape(train.shape[0], train.shape[1])
train_scaled = scaler.transform(train)
# 转换test data
test = test.reshape(test.shape[0], test.shape[1])
test_scaled = scaler.transform(test)
return scaler, train_scaled, test_scaled
# 逆缩放
def invert_scale(scaler, X, value):
new_row = [x for x in X] + [value]
array = numpy.array(new_row)
array = array.reshape(1, len(array))
inverted = scaler.inverse_transform(array)
return inverted[0, -1]
# fit LSTM来训练数据
def fit_lstm(train, batch_size, nb_epoch, neurons):
X, y = train[:, 0:-1], train[:, -1]
X = X.reshape(X.shape[0], 1, X.shape[1])
model = Sequential()
# 添加LSTM层
model.add(LSTM(neurons, batch_input_shape=(batch_size, X.shape[1], X.shape[2]), stateful=True))
model.add(Dense(1)) # 输出层1个node
# 编译,损失函数mse+优化算法adam
model.compile(loss='mean_squared_error', optimizer='adam')
for i in range(nb_epoch):
# 按照batch_size,一次读取batch_size个数据
model.fit(X, y, epochs=1, batch_size=batch_size, verbose=0, shuffle=False)
model.reset_states()
print("当前计算次数:"+str(i))
return model
# 1步长预测
def forcast_lstm(model, batch_size, X):
X = X.reshape(1, 1, len(X))
yhat = model.predict(X, batch_size=batch_size)
return yhat[0, 0]
# 加载数据
series = read_csv('data_set/shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True,
date_parser=parser)
# 让数据变成稳定的
raw_values = series.values
diff_values = difference(raw_values, 1)#转换成差分数据
# 把稳定的数据变成有监督数据
supervised = timeseries_to_supervised(diff_values, 1)
supervised_values = supervised.values
# 数据拆分:训练数据、测试数据,前24行是训练集,后12行是测试集
train, test = supervised_values[0:-12], supervised_values[-12:]
# 数据缩放
scaler, train_scaled, test_scaled = scale(train, test)
# fit 模型
lstm_model = fit_lstm(train_scaled, 1, 100, 4) # 训练数据,batch_size,epoche次数, 神经元个数
# 预测
train_reshaped = train_scaled[:, 0].reshape(len(train_scaled), 1, 1)#训练数据集转换为可输入的矩阵
lstm_model.predict(train_reshaped, batch_size=1)#用模型对训练数据矩阵进行预测
# 测试数据的前向验证,实验发现,如果训练次数很少的话,模型回简单的把数据后移,以昨天的数据作为今天的预测值,当训练次数足够多的时候
# 才会体现出来训练结果
predictions = list()
for i in range(len(test_scaled)):#根据测试数据进行预测,取测试数据的一个数值作为输入,计算出下一个预测值,以此类推
# 1步长预测
X, y = test_scaled[i, 0:-1], test_scaled[i, -1]
yhat = forcast_lstm(lstm_model, 1, X)
# 逆缩放
yhat = invert_scale(scaler, X, yhat)
# 逆差分
yhat = inverse_difference(raw_values, yhat, len(test_scaled) + 1 - i)
predictions.append(yhat)
expected = raw_values[len(train) + i + 1]
print('Moth=%d, Predicted=%f, Expected=%f' % (i + 1, yhat, expected))
# 性能报告
rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))
print('Test RMSE:%.3f' % rmse)
# 绘图
pyplot.plot(raw_values[-12:])
pyplot.plot(predictions)
pyplot.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
结果如下:
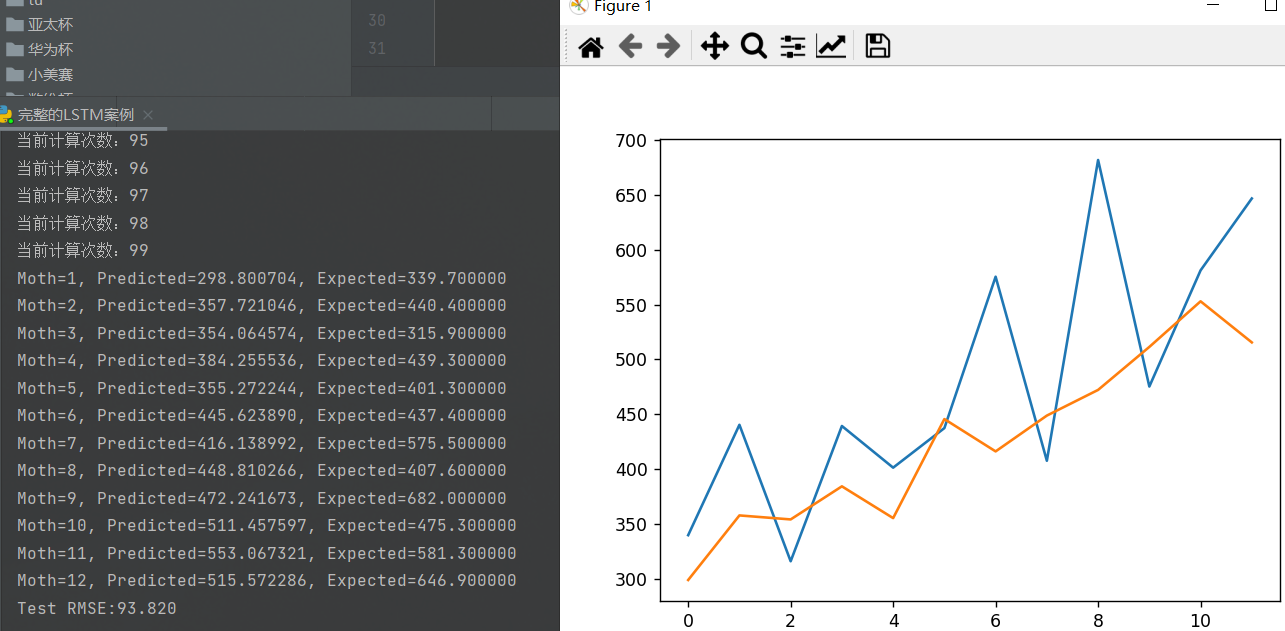
具体自己改改,给个参考。
完整文件:
链接:https://pan.baidu.com/s/1tYDb44Ge5S6Wwt1sPE8iHA?pwd=hkkc
提取码:hkkc
--来自百度网盘超级会员V3的分享
- 1
- 2
- 3
数模q un:912166339比赛期间禁止交流,赛后再聊,订阅本专栏,观看更多数学模型套路与分析。
更健壮的LSTM
数据集不变,代码如下:
# coding=utf-8
from pandas import read_csv
from pandas import datetime
from pandas import concat
from pandas import DataFrame
from pandas import Series
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from math import sqrt
from matplotlib import pyplot
import numpy
# 读取时间数据的格式化
def parser(x):
return datetime.strptime(x, '%Y/%m/%d')
# 转换成有监督数据
def timeseries_to_supervised(data, lag=1):
df = DataFrame(data)
columns = [df.shift(i) for i in range(1, lag + 1)] # 数据滑动一格,作为input,df原数据为output
columns.append(df)
df = concat(columns, axis=1)
df.fillna(0, inplace=True)
return df
# 转换成差分数据
def difference(dataset, interval=1):
diff = list()
for i in range(interval, len(dataset)):
value = dataset[i] - dataset[i - interval]
diff.append(value)
return Series(diff)
# 逆差分
def inverse_difference(history, yhat, interval=1): # 历史数据,预测数据,差分间隔
return yhat + history[-interval]
# 缩放
def scale(train, test):
# 根据训练数据建立缩放器
scaler = MinMaxScaler(feature_range=(-1, 1))
scaler = scaler.fit(train)
# 转换train data
train = train.reshape(train.shape[0], train.shape[1])
train_scaled = scaler.transform(train)
# 转换test data
test = test.reshape(test.shape[0], test.shape[1])
test_scaled = scaler.transform(test)
return scaler, train_scaled, test_scaled
# 逆缩放
def invert_scale(scaler, X, value):
new_row = [x for x in X] + [value]
array = numpy.array(new_row)
array = array.reshape(1, len(array))
inverted = scaler.inverse_transform(array)
return inverted[0, -1]
# fit LSTM来训练数据
def fit_lstm(train, batch_size, nb_epoch, neurons):
X, y = train[:, 0:-1], train[:, -1]
X = X.reshape(X.shape[0], 1, X.shape[1])
model = Sequential()
# 添加LSTM层
model.add(LSTM(neurons, batch_input_shape=(batch_size, X.shape[1], X.shape[2]), stateful=True))
model.add(Dense(1)) # 输出层1个node
# 编译,损失函数mse+优化算法adam
model.compile(loss='mean_squared_error', optimizer='adam')
for i in range(nb_epoch):
# 按照batch_size,一次读取batch_size个数据
model.fit(X, y, epochs=1, batch_size=batch_size, verbose=0, shuffle=False)
model.reset_states()
print("当前计算次数:"+str(i))
return model
# 1步长预测
def forcast_lstm(model, batch_size, X):
X = X.reshape(1, 1, len(X))
yhat = model.predict(X, batch_size=batch_size)
return yhat[0, 0]
# 加载数据
series = read_csv('data_set/shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True,
date_parser=parser)
# 让数据变成稳定的
raw_values = series.values
diff_values = difference(raw_values, 1)#转换成差分数据
# 把稳定的数据变成有监督数据
supervised = timeseries_to_supervised(diff_values, 1)
supervised_values = supervised.values
# 数据拆分:训练数据、测试数据,前24行是训练集,后12行是测试集
train, test = supervised_values[0:-12], supervised_values[-12:]
# 数据缩放
scaler, train_scaled, test_scaled = scale(train, test)
#重复实验
repeats = 30
error_scores = list()
for r in range(repeats):
# fit 模型
lstm_model = fit_lstm(train_scaled, 1, 100, 4) # 训练数据,batch_size,epoche次数, 神经元个数
# 预测
train_reshaped = train_scaled[:, 0].reshape(len(train_scaled), 1, 1)#训练数据集转换为可输入的矩阵
lstm_model.predict(train_reshaped, batch_size=1)#用模型对训练数据矩阵进行预测
# 测试数据的前向验证,实验发现,如果训练次数很少的话,模型回简单的把数据后移,以昨天的数据作为今天的预测值,当训练次数足够多的时候
# 才会体现出来训练结果
predictions = list()
for i in range(len(test_scaled)):
# 1步长预测
X, y = test_scaled[i, 0:-1], test_scaled[i, -1]
yhat = forcast_lstm(lstm_model, 1, X)
# 逆缩放
yhat = invert_scale(scaler, X, yhat)
# 逆差分
yhat = inverse_difference(raw_values, yhat, len(test_scaled) + 1 - i)
predictions.append(yhat)
expected = raw_values[len(train) + i + 1]
print('Moth=%d, Predicted=%f, Expected=%f' % (i + 1, yhat, expected))
# 性能报告
rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))
print('%d) Test RMSE:%.3f' %(r+1,rmse))
error_scores.append(rmse)
#统计信息
results = DataFrame()
results['rmse'] = error_scores
print(results.describe())
results.boxplot()
pyplot.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
文章来源: chuanchuan.blog.csdn.net,作者:川川菜鸟,版权归原作者所有,如需转载,请联系作者。
原文链接:chuanchuan.blog.csdn.net/article/details/123023199
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)