神经网络——单层感知器 10行代码完成初代神经网络
【摘要】 神经网络——单层感知器 10行代码完成初代神经网络
@[TOC](神经网络——单层感知器
1 感知器(Perceptron)
感知器(Perceptron)是一种具有单层计算单元的神经网络,只能用来解决线性可分的
二分类问题。在高维空间中的模式分类相当于用一个超平面将样本分开。如果二类模式
线性可分,则算法一定收敛。单层感知器的结构和功能都非常简单,在目前解决实际问
题中很少被采用,但是由于其较易学习和理解,是研究其他网络的基础。
2 研究步骤
- 理解结构,类似于之前的神经元模型,用于解决二分类线性可分问题,或者是线性函
数逼近问题 - 确定激活函数,这里常用的是单极性(或双极性)阈值函数:

3 确定输出的计算公式:

- 确定权值调整公式:先要定义学习信号,这里学习信号定义为期望输出和实际输出的
差: 。则权值调整公式为;

4 学习算法步骤
1 观察输入向量,一般需要标准化,当量纲差别不大时不需要标准化。
2 初始化:
- 选取学习率η(0 < η < 1),η值太大会影响训练的稳定性、太小会降低收敛速度
- 初始化权值向量Wj = (ω0j ,ω1j ,ω2j , . . . ,ωnj )T
, 设置为全零值或者较小的非零随
机数 - 设定精度控制参数ϵ(相应的循环时精度控制变量d = ϵ + 1) - 设定最大迭代次数M
计算输出:输入样本:
,计算出节点j的实际输出:
4 根据选择的学习方法调整权值:
,其中
是第 个样本在
j节点 的期望输出
5 循环调整权值直到满足收敛条件,终止循环。收敛条件是:
误差小于某个预先设定的精度控制参数:
(这里为了防止偶然因素
导致的提前收敛,可以设定误差连续若干次小于 ,为了防止算法不一定收敛而
进入死循环), 或者是累积误差小于精度控制参数:
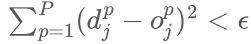
迭代次数达到设定值 (可以两个条件混合使用)
3 R 代码实现
使用R自带的数据集iris,划分x和y
# Take iris as an example
#clean resources
rm(list=ls())
#display the first 5 items
head(iris)
adata<-iris[,1:4]
colnames(adata)<-c("x1","x2","x3","y")
标准化数据消除量纲的影响
#Standardized data
adata[,1:3]<-scale(adata[,1:3])
设置 为阈值,(类比线性回归截距项),使得系数更加自由(没有 一定回过原点,给函数加了限制条件,设置 函数更自由)
adata<-cbind(x0=1,adata)
#select stop residual
初始化残差和,学习率,随机权重
eps=5.5
#initialization residuals
d=eps+1
##learning efficient
eta=0.005
##random weight
w=runif(4,0,1)
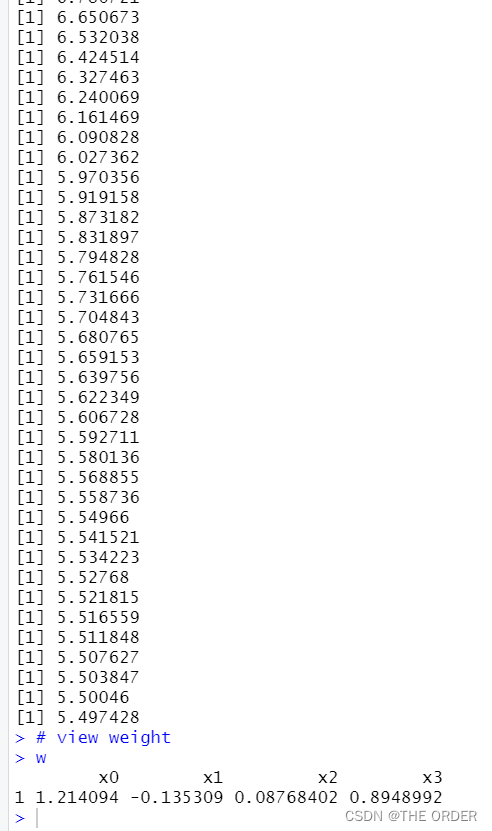
依靠公式进行感知器神经网络
while(d>=eps and i <200){
d<-0;i=1
for(i in 1:nrow(adata)){
xi=adata[i,1:4]
delta=adata[i,5]-sum(xi*w)
w=w+eta*delta*xi
d=d+delta^2
}
i=i+1
print(d)
}
# view weight
w
#Residual sum
sum((adata[,5]-(as.matrix(adata[,1:4]))%*%t(w))^2)
#linear regression
lma<-lm(y~x1+x2+x3,data=adata)
lma
sum(summary(lma)$residual^2)

对比和线性回归的区别,发现和线性回归差别不大,线性回归更优(因为线性回归是最小二乘法得出的最优解)
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者

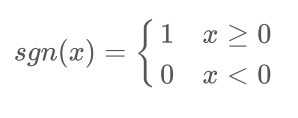
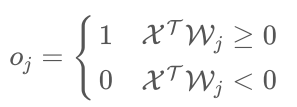
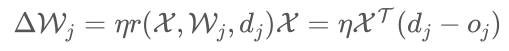

评论(0)