matplotlib绘制箱形图之基本配置——万能模板案例
【摘要】
目录
线形图介绍
参数说明
绘制单个线形图
绘制多个线形图
模板案例
直接使用plt.boxplot(df['列名'])
绘制水晶形式箱形图
使用seaborn进行绘制
线形图的直观可视化
加一组直方图
剖析线形图的原理
数据库分析实际案例
总结
每文一语
线形图介绍
箱形图（Box-plot）盒式图或...
目录
线形图介绍
箱形图（Box-plot）盒式图或箱线图，是一种用作显示一组数据分散情况资料的统计图。因形状如箱子而得名。在各种领域也经常被使用，常见于品质管理。
它主要用于反映原始数据分布的特征，还可以进行多组数据分布特征的比较。
箱线图的绘制方法是：先找出一组数据的上边缘、下边缘、中位数和两个四分位数；然后， 连接两个四分位数画出箱体；再将上边缘和下边缘与箱体相连接，中位数在箱体中间。
参数说明
boxplot(
x, notch=None, sym=None, vert=None, whis=None,
positions=None, widths=None, patch_artist=None,
bootstrap=None, usermedians=None, conf_intervals=None,
meanline=None, showmeans=None, showcaps=None, showbox=None,
showfliers=None, boxprops=None, labels=None, flierprops=None,
medianprops=None, meanprops=None, capprops=None,
whiskerprops=None, manage_ticks=True, autorange=False,
zorder=None, *, data=None):
x：指定要绘制箱线图的数据，可以是一组数据也可以是多组数据；
notch：是否以凹口的形式展现箱线图，默认非凹口；
sym：指定异常点的形状，默认为蓝色的+号显示；
vert：是否需要将箱线图垂直摆放，默认垂直摆放；
whis：指定上下须与上下四分位的距离，默认为1.5倍的四分位差；
positions：指定箱线图的位置，默认为range(1, N+1)，N为箱线图的数量；
widths：指定箱线图的宽度，默认为0.5；
patch_artist：是否填充箱体的颜色，默认为False；
meanline：是否用线的形式表示均值，默认用点来表示；
showmeans：是否显示均值，默认不显示；
showcaps：是否显示箱线图顶端和末端的两条线，默认显示；
showbox：是否显示箱线图的箱体，默认显示；
showfliers：是否显示异常值，默认显示；
boxprops：设置箱体的属性，如边框色，填充色等；
labels：为箱线图添加标签，类似于图例的作用；
filerprops：设置异常值的属性，如异常点的形状、大小、填充色等；
medianprops：设置中位数的属性，如线的类型、粗细等；
meanprops：设置均值的属性，如点的大小、颜色等；
capprops：设置箱线图顶端和末端线条的属性，如颜色、粗细等；
whiskerprops：设置须的属性，如颜色、粗细、线的类型等；
manage_ticks：是否自适应标签位置，默认为True；
autorange：是否自动调整范围，默认为False；
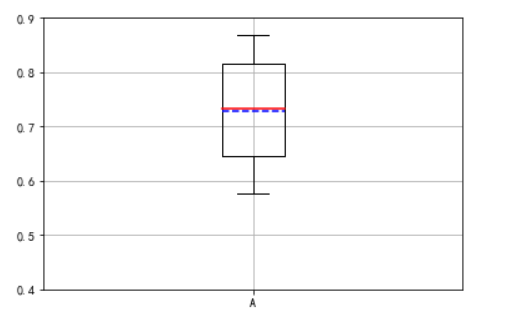
绘制单个线形图
labels = 'A'
data = [0.8685, 0.6671, 0.7971, 0.5774]
plt.grid(True) # 显示网格
plt.boxplot(data,
medianprops={'color': 'red', 'linewidth': '1.5'},
meanline=True,
showmeans=True,
meanprops={'color': 'blue', 'ls': '--', 'linewidth': '1.5'},
flierprops={"marker": "o", "markerfacecolor": "red", "markersize": 10},
labels=labels)
plt.yticks(np.arange(0.4, 0.91, 0.1))
plt.show()
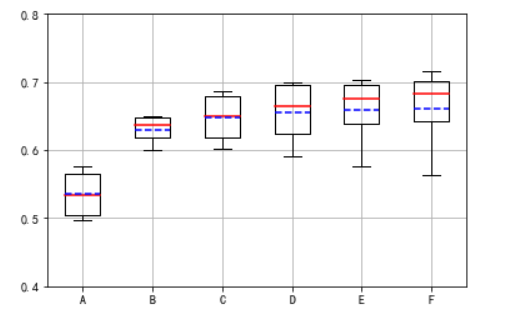
绘制多个线形图
labels = 'A', 'B', 'C', 'D', 'E', 'F'
A = [0.4978, 0.5764, 0.5073, 0.5609]
B = [0.5996, 0.65, 0.6251, 0.6473]
C = [0.6015, 0.687, 0.6237, 0.6761]
D = [0.5918, 0.6999, 0.6343, 0.6947]
E = [0.577, 0.6932, 0.6593, 0.7036]
F = [0.5637, 0.7161, 0.6683, 0.697]
plt.grid(True) # 显示网格
plt.boxplot([A, B, C, D, E, F],
medianprops={'color': 'red', 'linewidth': '1.5'},
meanline=True,
showmeans=True,
meanprops={'color': 'blue', 'ls': '--', 'linewidth': '1.5'},
flierprops={"marker": "o", "markerfacecolor": "red", "markersize": 10},
labels=labels)
plt.yticks(np.arange(0.4, 0.81, 0.1))
plt.show()
模板案例
直接使用plt.boxplot(df['列名'])
groups = df.groupby('OPERATOR', as_index=False)
boxes = [] # 列表(box1,box2,box3,...)
boxes_label = []
for 销售员, df_销售员 in groups: # groupby得到的每一个group包含了分组的键值和被分组的数据
boxes.append(df_销售员['PRICE'])
boxes_label.append(销售员)
plt.figure(figsize=(15,7))
plt.boxplot(boxes,vert=False,whis=2,showmeans=True,showbox = True) # 只调用依次boxplot画多组箱型图
plt.yticks(range(1,len(boxes_label)+1),boxes_label,fontsize=15.0)
plt.xticks(np.arange(0,11000,step=1000))
plt.xlabel('销售额',fontsize=15.0)
plt.ylabel('销售人员',fontsize=15.0)
plt.title('销售人员的销售业绩分析',fontsize=20.0)
plt.show()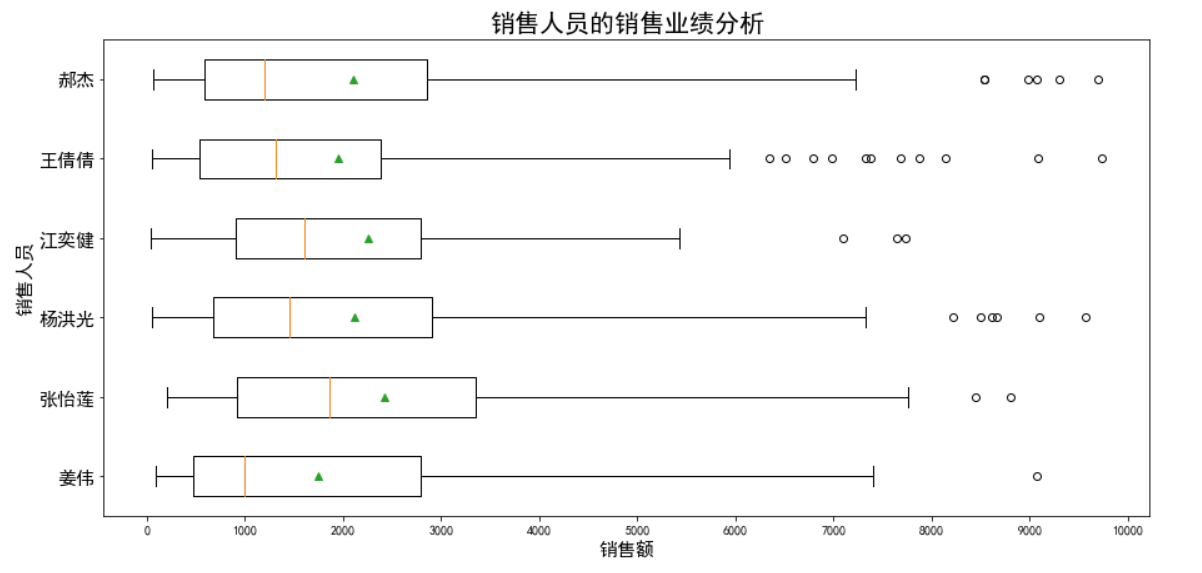
绘制水晶形式箱形图
plt.figure(figsize=(15,7))
plt.violinplot(boxes,vert=True,showmeans=True) # 只调用依次boxplot画多组箱型图
plt.xticks(range(1,len(boxes_label)+1),boxes_label,fontsize=15.0)
plt.yticks(np.arange(0,11000,step=1000))
plt.ylabel('销售额',fontsize=15.0)
plt.xlabel('销售人员',fontsize=15.0)
plt.title('销售人员的销售业绩分析',fontsize=20.0)
plt.show()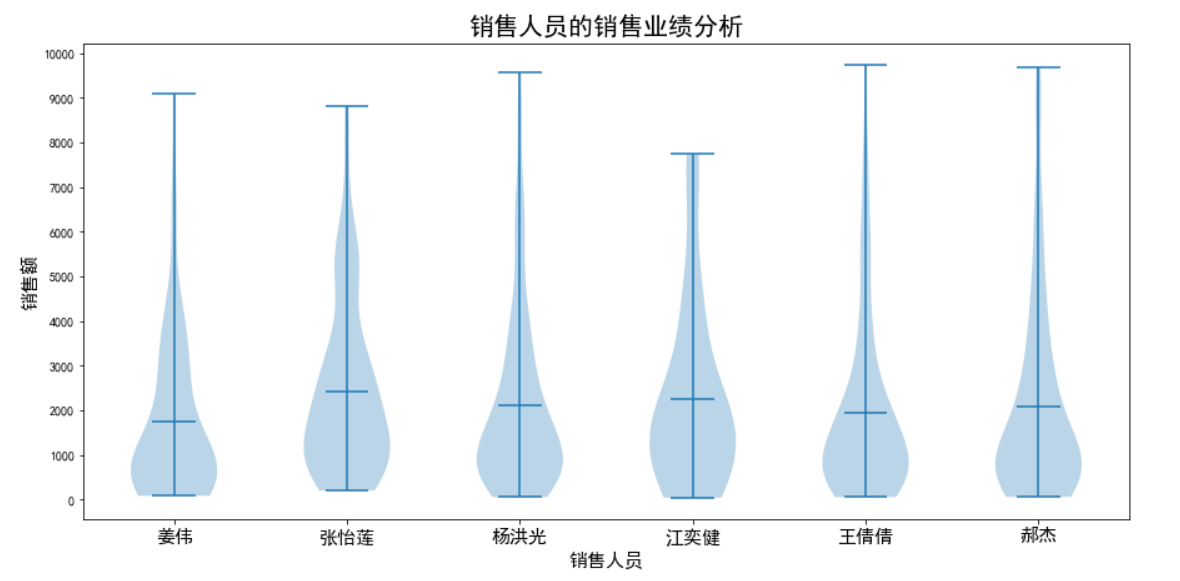
使用seaborn进行绘制
plt.figure(figsize=(10,16))
tips["weekend"] = tips["day"].isin(["Sat", "Sun"])
plt.subplot(321)
sns.barplot(data=tips,x="day", y="total_bill", hue="weekend", dodge=False)
plt.subplot(322)
sns.pointplot(data=tips,x="day", y="total_bill", hue="weekend", dodge=False)
plt.subplot(323)
sns.boxplot(data=tips,x="day", y="total_bill", hue="weekend", dodge=False)
plt.subplot(324)
sns.violinplot(data=tips,x="day", y="total_bill", hue="weekend", dodge=False)
plt.subplot(325)
sns.stripplot(data=tips,x="day", y="total_bill", hue="weekend", dodge=False)
plt.subplot(326)
sns.swarmplot(data=tips,x="day", y="total_bill", hue="weekend", dodge=False)
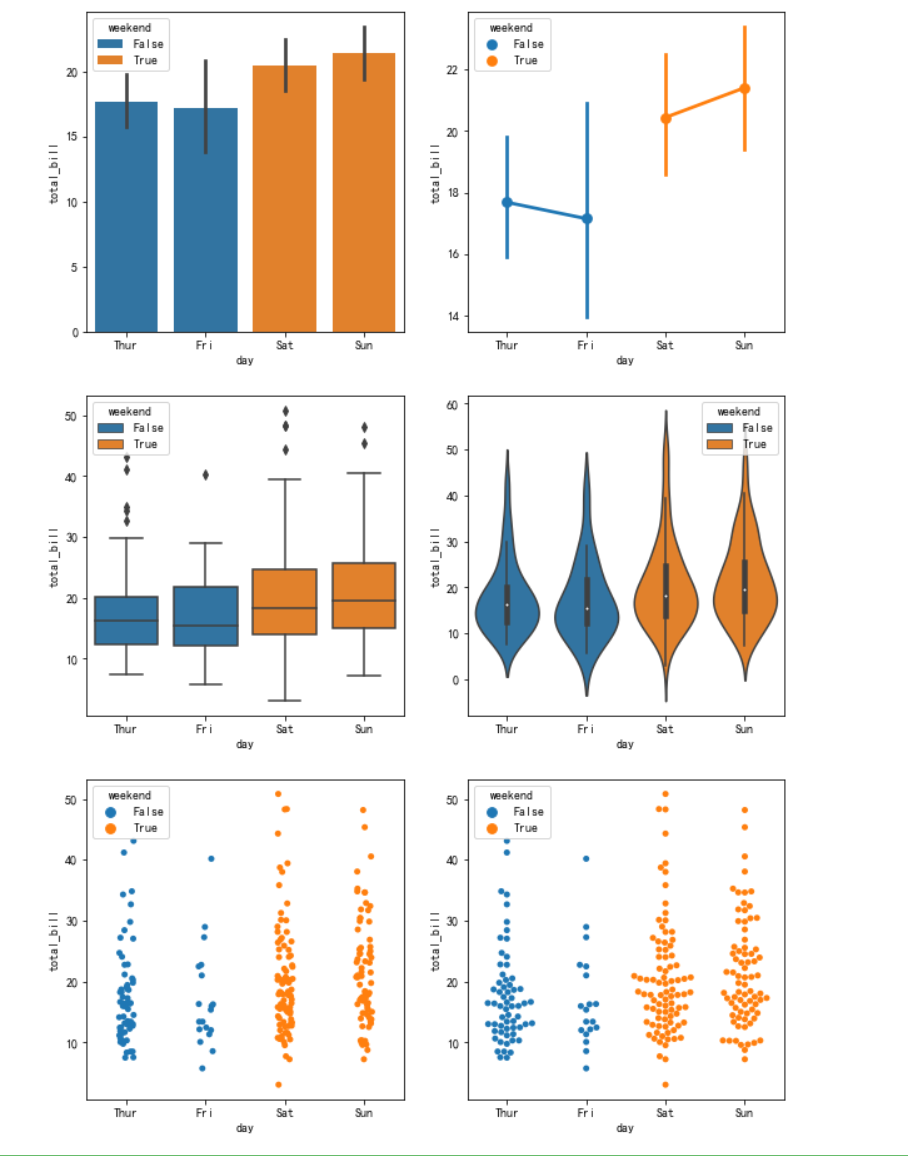
fig = plt.figure(figsize=(10,5))
sns.violinplot(data=df,x='PROD_TYPE',y='PRICE',figure=fig)
#sns.violinplot(data=df,x='OPERATOR',y='PROFIT',figure=fig)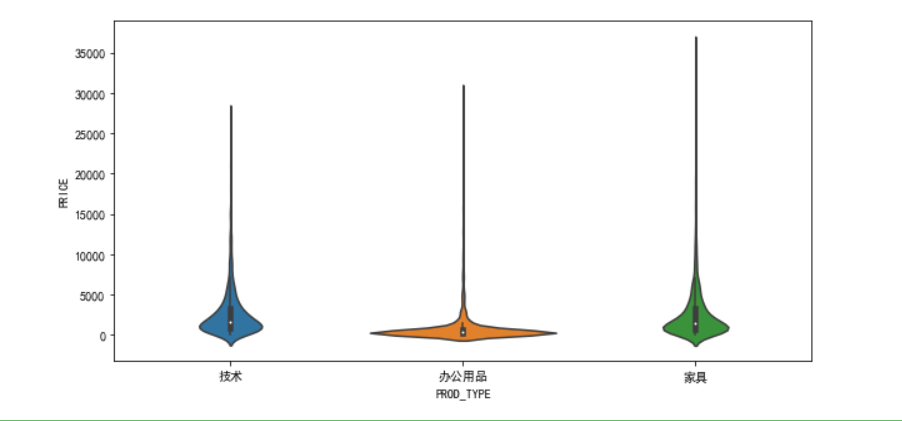
可能看到这里，有些小伙伴都没有理解绘制线形图的要点和精髓，那么下面我们继续在此基础上研究图形的配置和数据源的选择！
线形图的直观可视化
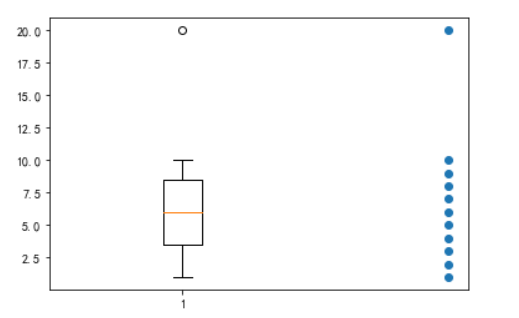
plt.boxplot([1,2,3,4,5,6,7,8,9,10,20]) # 箱型图
plt.scatter(np.full(11,2),[1,2,3,4,5,6,7,8,9,10,20]) # 散点图加一组散点图和线形图进行对比，我们发现线形图反映的是数据的分布特点，也就是我们散点图的可视化，只不过，线形图有更好的指标让我们一目了然的去看出数据的特点。
加一组直方图
N = np.random.randn(1000)*0.5 # Normal 产生1000各满足正态分布的随机数数组
plt.figure(dpi=120)
plt.boxplot(N)
plt.scatter(np.full_like(N,2),N,s=0.3,alpha=0.5,)
plt.hist(N,orientation='horizontal',density=True)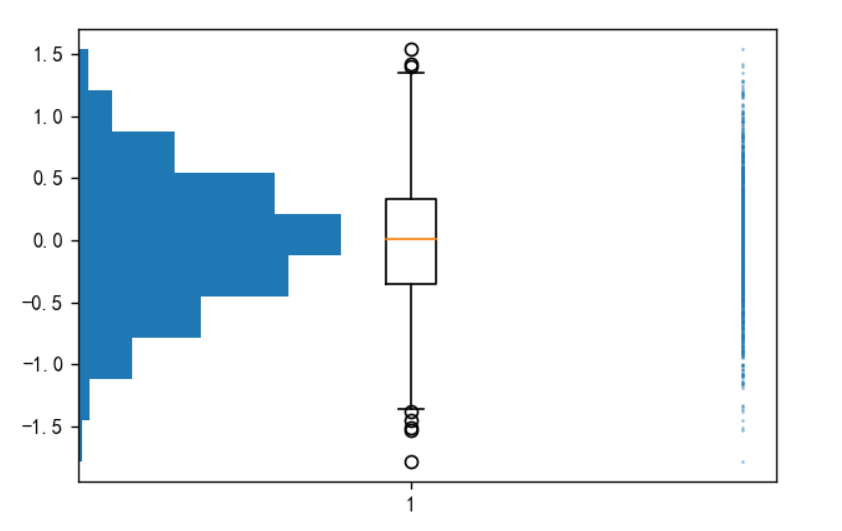
剖析线形图的原理
N = [ -2,1,3,4,5,6,7,8,9, 17, 20]
Q0 = np.quantile(N,q=0/4) # 最小值
Q1 = np.quantile(N,q=1/4) # 箱子的下边
Q2 = np.quantile(N,q=2/4) # 箱子的中位数线
Q3 = np.quantile(N,q=3/4) # 箱子的上边
Q4 = np.quantile(N,q=4/4) # 最大值
M = np.mean(N)
IQR = Q3-Q1 # 箱子的长度
Upper = Q3 + 1.5*IQR # 箱线图的上限 (限制，如果值超过这个限度，就是异常值)
Lower = Q1 - 1.5*IQR # 箱线图的下限 (限制，如果值不超过这个限度，就取不超限的最小值)
print(f"Q3={Q3}, Q1={Q1}, IQR={IQR}, Upper={Upper}, Lower={Lower},M={M} ")
plt.figure(dpi=120)
plt.boxplot(N,meanline=True,showmeans=True)
plt.yticks([0,Lower,Q0,Q1,M,Q2,Q3,Q4,Upper],['0','Lower','Q0','Q1','M','Q2','Q3','Q4','Upper'])
plt.grid(axis='y')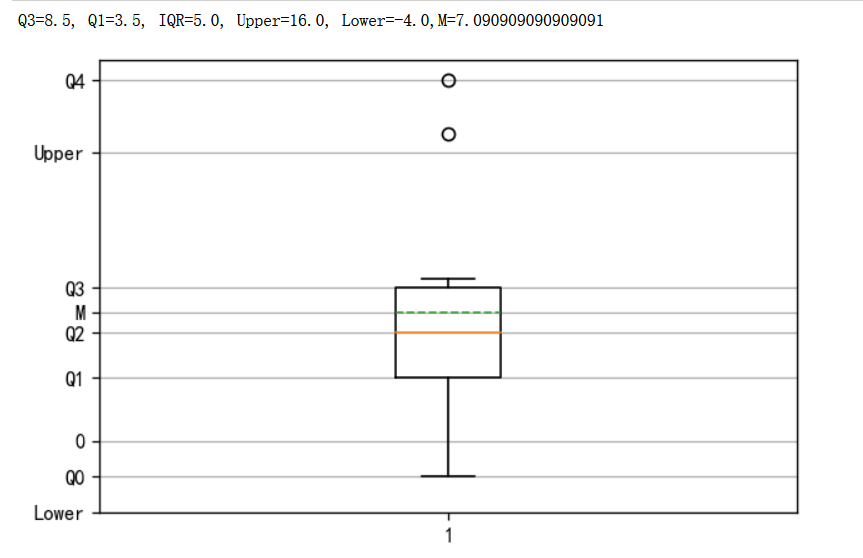
N = [0,1,3,4,5,9,10,20]
Q0 = np.quantile(N,q=0/4) # 最小值
Q1 = np.quantile(N,q=1/4) # 箱子的下边
Q2 = np.quantile(N,q=2/4) # 箱子的中位数线
Q3 = np.quantile(N,q=3/4) # 箱子的上边
Q4 = np.quantile(N,q=4/4) # 最大值
M = np.mean(N) # 均值
IQR = Q3-Q1 # 箱子的长度
Upper = Q3 + 1.5*IQR # 箱线图的上限 (限制，如果值超过这个限度，就取这个限度)
Lower = Q1 - 1.5*IQR # 箱线图的下限 (限制，如果值不超过这个限度，就取不超限的最值)
print(f"Q3={Q3}, Q1={Q1}, IQR={IQR}, Upper={Upper}, Lower={Lower},M={M} ")
plt.boxplot(N,showmeans=True)
plt.yticks([0,Lower,Q0,Q1,M,Q2,Q3,Q4,Upper])
plt.grid(axis='y')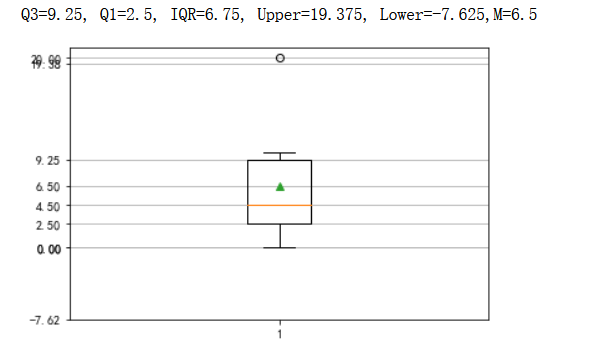 
直接使用sns和plt绘制
plt.subplot(121)
sns.boxplot(df["PROFIT"].values,showfliers=False)
plt.subplot(122)
plt.boxplot(df['PROFIT'],showfliers=False)数据库分析实际案例
import pymysql
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'KaiTi'
plt.rcParams['axes.unicode_minus'] = False
# 连接数据库
db = pymysql.connect(host='172.19.21.249',user='root',password='root',database='testdb')
# 构造sql查询
sql = "select OPERATOR 销售人员, PRICE 销售额 FROM orders where FY='2019'"
# 执行sql查询获取结果
df = pd.read_sql_query(sql,db)
operators = df['销售人员'].unique()
boxes = []
for op in operators:
boxes.append(df[df['销售人员']==op]['销售额'])
plt.boxplot(boxes, labels=operators, showfliers=False,showmeans=True)
counts = df.groupby('销售人员').count()
plt.plot(np.arange(1,counts.shape[0]+1),counts)
plt.show()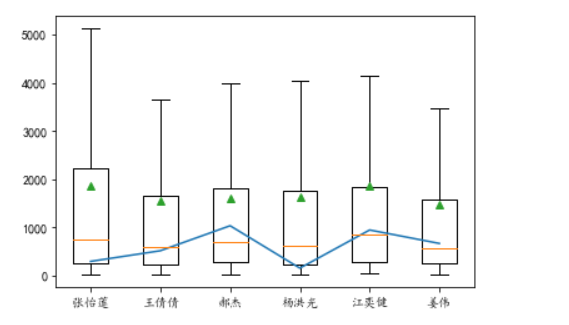
总结
通过这么多的案例，我们应该明确到线形图绘制的基本语法有哪些。如何直接通过数据源就可以对其进行可视化，一般来说，线形图的用处主要是用来发掘异常值和异常点的，在科研统计中用的比较多。
每文一语
有的放矢
文章来源: wxw-123.blog.csdn.net，作者：王小王-123，版权归原作者所有，如需转载，请联系作者。
原文链接：wxw-123.blog.csdn.net/article/details/124061100
【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）