连通块(dfs)java实现
🙊🙊作者主页:🔗
📔📔 精选专栏:🔗
📋📋 精彩摘要:Spring AOP面向切面编程是Java OOP面向对象编程的延续,是软件开发中的一个热点,也是Spring框架中的一个重要内容,是函数式编程的一种衍 生范型。利用AOP可以对业务逻辑的各个部分进行隔离,从而使得业务逻辑各部分之间的耦合度降低,提高程序的可重用性,同时提高了开发的效率。
💞💞觉得文章还不错的话欢迎大家点赞👍➕收藏⭐️➕评论💬支持博主🤞
目录
前言
连通块问题属于图的深度优先遍历dfs,本文章通过求连通块的个数简单案例,来介绍dfs解决连通块问题。
例题链接
例题中给到的是char类型地图,' . ' 代表不通路,' W ' 代表可连通,具体情况根据题目给的进行修改。
什么是连通块
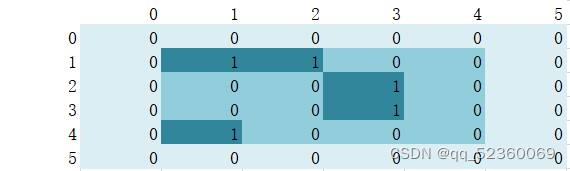
如图整个表格为一个5*5二维数组,用来表示整个地图,白色填充为二维数组下标,最外层浅绿色代表地图的边界(为什么创建边界下文有提到),较为深颜色的为存放数据的二维数组,即下标(1~4)*(1~4)。而颜色最深的块就是连通块,图中给出的就有三个连通块(上下左右连通,不考虑斜对连通)。
具体思路
除了行数列数以及开辟二维数组地图,还需要一个与地图同样大小的二维数组visitied,用来表示当前节点是否已经被访问过了。具体思路同图的dfs类似,当遍历到一个结点为1表示该节点可以连通(根据题目给的可能不同)并且没被访问过就进行深度遍历。
具体看代码。
代码
注意
在实际应用时,为了防止当结点位于边界时,例如结点下标为(0,0),其左结点下标为(-1,0),这时-1会越界。因此开辟二维数组的大小总是比题目中给到的n*m多两行,即开辟(n+2)*(m+2)大小的二维数组。
- 点赞
- 收藏
- 关注作者


评论(0)