数据结构从入门到精通(第六篇) :堆的实现
【摘要】 堆的概念如果有一个关键码的集合K = { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足: <= 且 <= ( >= 且 >= ) i = 0,1,2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。性质:堆中某个节点的值总是不大于或不小于其父节点的值堆总是一棵完全二叉树 堆的实现(大堆) 接口//堆初...
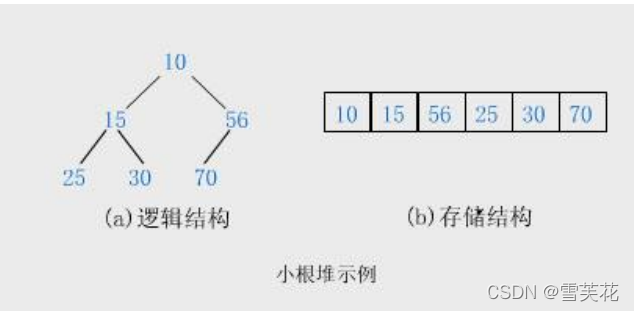
堆的概念
如果有一个关键码的集合K = { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储
在一个一维数组中,并满足: <= 且 <= ( >= 且 >= ) i = 0,1,
2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
- 性质:
-
- 堆中某个节点的值总是不大于或不小于其父节点的值
-
- 堆总是一棵完全二叉树
堆的实现(大堆)
接口
//堆初始化
void HeapInit(HP* hp);
//堆销毁
void HeapDestroy(HP* hp);
//入堆
void HeapPush(HP* hp, HPDataType x);
//出堆
void HeapPop(HP* hp);
//堆数据打印
void HeapPrint(HP* hp);
//堆顶数据
HPDataType HeapTop(HP* hp);
//堆存入数据个数
int HeapSize(HP* hp);
// 堆的判空
bool HeapEmpty(HP* hp);
//交换函数
void Swap(HPDataType* a, HPDataType* b);
//数据向上调整
void AdjustUp(HPDataType* a, int child);
//数据向下调整
void AdjustDown(HPDataType* a, int size, int parent);
堆结构创建
下面我们给出一个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆,现在我们通过算
法,把它构建成一个堆。根节点左右子树不是堆,我们怎么调整呢?这里我们从倒数的第一个非叶子节点的
子树开始调整,一直调整到根节点的树,就可以调整成堆。
//默认堆中的数据类型
typedef int HPDataType;
//堆结构体类型
typedef struct Heap
{
HPDataType* a;//数组指针(指向动态开辟的空间)
int size;//堆中存放的数据个数
int capacity;//堆的容量(数组长度)
}HP;

堆的初始化
//堆初始化
void HeapInit(HP* hp)
{
assert(hp);//避免传入参数错误
//初始化
hp->a = NULL;
hp->size = hp->capacity = 0;
}
堆的销毁
//堆销毁
void HeapDestroy(HP* hp)
{
assert(hp);//避免传入参数错误
//释放
free(hp->a);
hp->a=NULL;//置空
hp->capacity=hp->size=0;
}
入堆
- 这里采用的入堆方式是现将入堆数据先放在堆存储数据最尾部的后一个位置, 再从这个位置进行向上调整,直到符合大堆的存储要求
//入堆
void HeapPush(HP* hp, HPDataType x)
{
assert(hp);//避免传入参数错误
//满堆的情况
if (hp->size == hp->capacity)
{
//如果容量为0则开辟4个空间,否则扩展成原来的两倍
int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
HP* tmp = (HP*)realloc(hp->a, sizeof(HP) * newcapacity);
if (tmp == NULL)//开辟失败则打印错误并结束进程
{
perror("realloc fail:");
exit(-1);
}
hp->capacity = newcapacity;//更新数据
hp->a = tmp;
}
//入堆操作
hp->a[hp->size] = x;//先放入尾端,再调整
hp->size++;
//数据调整
AdjustUp(hp->a, hp->size - 1);//传入数组地址和下标
}
堆向上调整
- 依据父子节点位置,找到对应下标进行比较数据
- 如果数据不符合大堆则进行交换,直到交换成符合大堆
- 当入堆的数据到下标为0时或者符合大堆时停止交换
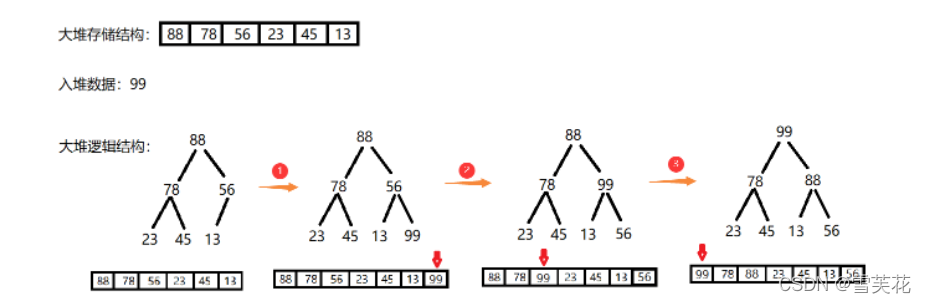
- 代码:
//交换函数
void Swap(HPDataType* a, HPDataType* b)
{
HPDataType tmp = *a;
*a = *b;
*b = tmp;
}
//数据调整
void AdjustUp(HPDataType* a, int child)//
{
int parent = (child - 1) / 2;
while (child)
{
if (a[parent] < a[child])//不符合情况交换
Swap(&a[parent], &a[child]);
else
break;
//调整下标
child = parent;
parent = (child - 1) / 2;
}
}
堆的pop
- 出堆方式:
- 首先我们将堆顶数据也就是下标为0的数据与堆尾数据交换
- 交换后让记录存入数据的变量减减,实现删除堆顶数据
- 再让现在堆顶的数据向下调整
- 代码:
//出堆(删除堆顶的数据)
void HeapPop(HP* hp)
{
assert(hp);//避免传入参数错误
assert(hp->size);//空堆的情况
Swap(&hp->a[0], &hp->a[hp->size - 1]);//先将堆顶数据与堆尾交换
hp->size--;//再将记录数据个数变量减减实现删除的效果
//对现在堆顶的数据进行下调
AdjustDown(hp->a, hp->size, 0);
}
向下调整数据
- 同样的依据父子节点位置,找到对应下标进行比较数据
- 因为堆是一个完全二叉树,需要考虑存在只有左子节点没有右子节点的情况
- 如果左右子节点都存在,那么与左右子节点中数据大的节点进行比较
- 如果数据不符合大堆则进行交换,直到交换成符合大堆
- 当比较的子树下标超出存储数据个数时或者符合大堆时停止交换
代码:
//数据调整
void AdjustDown(HPDataType* a, int size, int parent)
{
int child = parent * 2 + 1;
while (child<size)
{
//找到数据大的儿子
if (child + 1 < size && a[child + 1] > a[child])
{
child++;
}
//将父节点与大子节点交换
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);//交换数据
parent = child;//调整下标位置
child = parent * 2 + 1;
}
else
{
break;//结束调整
}
}
}
建堆时间复杂度的计算
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的
就是近似值,多几个节点不影响最终结果):
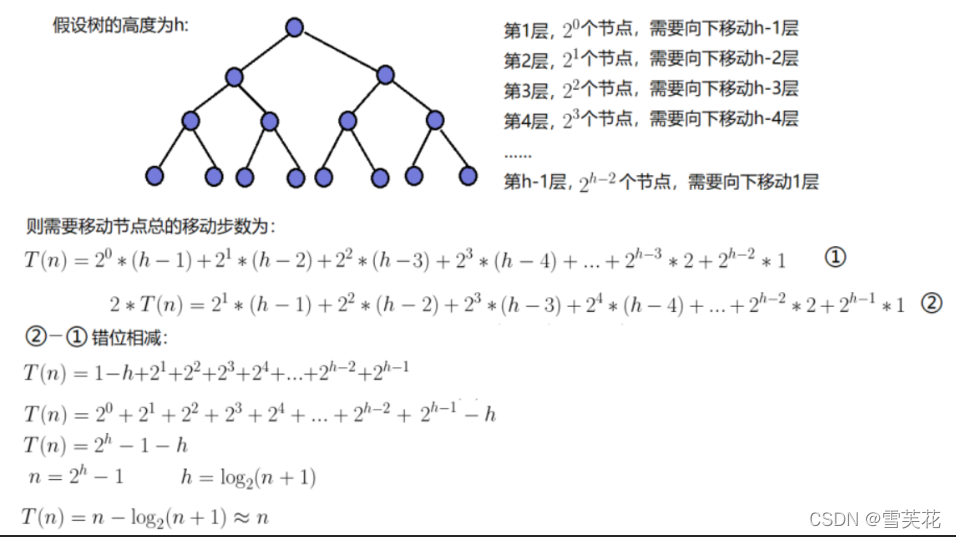
建堆的时间复杂度为O(N)。
总结
- 本篇主要讲的是堆的实现和结构特点
- 但对堆的具体性质和用法 暂未讲解
- 堆的具体性质和用法会放在下一篇***堆的应用***来讲解,敬请期待吧 b( ̄▽ ̄)d
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)