【每日一题】备战冲击蓝桥杯国赛——Python程序设计 | Day15 | 回路计数 | 真题代码解析
每天刷一道题,话不多说,先刷近两年的题吧,现在是2021年的真题了,如果有一起的可以加入我们!!!
一起来刷题,冲击国赛!!!
2021年第十二届蓝桥杯赛题总览
2020年的题就是这些,类型分为两种,分别是结果填空和程序设计,我们每天刷一道题,省赛没问题!
回路计数 (题目)
(本题总分:15分)
官方练习系统:https://www.lanqiao.cn/problems/1462/learning/
—>【问题描述】

—>【结果描述】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
解析
通过阅读题干,本题——难度中等:⭐⭐⭐
考察类型:动态规划、数论
考察知识点:互质、dp
分析:
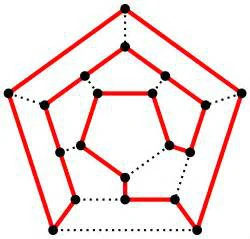
今天的题有点儿意思,一共有21栋楼,编号从1~21,两栋楼a和b之间,如果a和b互质则连通(有一条走廊)。不禁让人想到,互质?诶!什么是互质呢?
互质:互质是公约数只有1的两个整数,叫做互质整数。公约数只有1的两个自然数,叫做互质自然数,后者是前者的特殊情形。
重点来了,走一条哈密尔顿回路。那现在又有疑问了?什么是哈密尔顿回路呢?
哈密顿图(哈密尔顿图)(英语:Hamiltonian graph,或Traceable graph)是一个无向图,由天文学家哈密顿提出,由指定的起点前往指定的终点,途中经过所有其他节点且只经过一次。在图论中是指含有哈密顿回路的图,闭合的哈密顿路径称作哈密顿回路(Hamiltonian cycle),含有图中所有顶点的路径称作哈密顿路径(Hamiltonian path)。
现在大概意思已经明白了 。这里直接引用大佬的解释:
- 一共有2的21次方种状态(从全为0到全为21个1),用二进制表示,例如00000000000000000001,每一位代表一栋教学楼,该位置上为1代表该教学楼已经遍历过,0代表该教学楼没有遍历过。
- 最终的目标为1111·····111(21个1),由于我们从第一栋教学楼出发的,因此初始首位就有一个1(初始状态,即第2种状态,000······0001)
- 每一种状态对应一种遍历的中途过程。
- dp[i][j]存储了第i+1个状态,并且该状态以第j+1栋教学楼为终止节点的方案数。对于某一种状态,由于遍历顺序的不同,因此终止节点可能不同。
- dp[1][0]=1,该等式左边表示第2种状态(000······1),且该状态以第一栋教学楼为终止节点的方案数,并赋值为1.我们就是从第一栋教学楼出发的,这可以理解。
- 状态之间具有转化关系(这里是节点数相差为1的状态间的转化)。例如:000···111(dp[7])可能从000······110(dp[6])、000······101(dp[5])、000······011(dp[3])转化而来。可以看出是其中一个0变成了1.而转化过程与连通与否相关。因此要考虑转化前后状态的具体终止结点,二者互质才可连通。
- 于是,从dp[1]开始递推,最终得到dp[m-1](m为2的21次方),随谓dp[m-1],是一个列表,列表中的元素(数字)代表方案数,以不同教学楼为终止节点的方案数,111······111,该列表有21个元素。得到111······111该状态后,并不是最终结果,因为该状态只是表明所有教学楼都只走过一遍,但没有回到第一栋教学楼,由于1和任何数互质,因此无论以哪一栋教学楼为终止节点(只要不是第一栋教学楼),就能回到起点。
- sum(dp[m - 1]) - dp[m - 1][0]即为最终答案。
下面直接开干!!!
代码
Python代码实现:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2022/3/9 15:22
# @Author : 府学路18号车神
# @Email :yurz_control@163.com
# @File : Day15.py
from math import gcd # 导入函数求解最大公约数
from time import time
n = 21 # 输入栋数
m = 1 << n
dp = [[0 for j in range(n)] for i in range(m)] # #dp[i][j]对于状态i,i的二进制表示中为1的位置 表示走过了教学楼j
load = [[False for a in range(n)] for b in range(n)]
start_time = time()
for a in range(1, n+1):
for b in range(1, n+1):
if gcd(a, b) == 1: # 如果a和b之间的最大公约数为1,则表示互质
load[a-1][b-1] = True
dp[1][0] = 1 # 从第一栋楼出发
for a in range(1, m):
for b in range(1, m):
if a >> b & 1: # 判断状态i是否包含第j栋教学楼
for k in range(n): # 枚举所有可能从教学楼k走到教学楼j的情况
if a - (a<<b) >> k & a and load[k][b]:
dp[a][b] += dp[a-(1<<b)][k]
end_time = time()
print("总共耗时:", end_time-start_time)
print(sum(dp[m-1]) - dp[m-1][0]) # 计算时间很长, 结果为:881012367360

可以得出最终的结果为:881012367360
由此,我们可以快速得出结果,验证完毕!
今天开刷第 十五 天,欢迎大家加入,一起变强,一起自律,一起上国赛!!!
有不同解法的可以在下面留言哦!~
往期刷题路线:
| 刷题路线 | Detail |
|---|---|
| 2020年 | |
| Day-01 | 门牌制作 |
| Day-02 | 寻找2020 |
| Day-03 | 跑步锻炼 |
| Day-04 | 蛇形填数 |
| Day-05 | 排序 |
| Day-06 | 装饰珠 |
| Day-07 | 成绩统计 |
| Day-08 | 单词分析 |
| Day-09 | 数字三角形 |
| Day-10 | 平面切分 |
| – | – |
| 2021年 | |
| Day-11 | 卡片 |
| Day-12 | 直线 |
| Day-13 | 货物摆放 |
| Day-14 | 路径 |
官方刷题练习系统:http://lx.lanqiao.cn/
❤坚持读Paper,坚持做笔记,坚持学习,坚持刷力扣LeetCode❤!!!
坚持刷题!!!冲击国赛
⚡To Be No.1⚡⚡哈哈哈哈
⚡创作不易⚡,过路能❤关注、收藏、点个赞❤三连就最好不过了
ღ( ´・ᴗ・` )
❤
- 点赞
- 收藏
- 关注作者


评论(0)