机器学习推荐算法之关联规则Apriori与FP-Growth算法详解
目录
Apriori算法介绍
Apriori,中文是先验,开始的意思。这个算法为了规避前面说到的指数爆炸的问题,采取了提前剪枝的办法。核心是两条定律:
定律一:如果一个集合是频繁项集,则它的所有子集都是频繁项集。
定律二:如果一个集合不是频繁项集,则它的所有超集都不是频繁项集。
Apriori定律举例
举例1:假设一个集合{A,B}是频繁项集,即A、B同时出现在一条记录的次数大于等于最小支持度min_support,则它的子集{A},{B}出现次数必定大于等于min_support,即它的子集都是频繁项集。
Apriori定律举例
举例2:假设集合{A}不是频繁项集,即A出现的次数小于min_support,则它的任何超集如{A,B}出现的次数必定小于min_support,因此其超集必定也不是频繁项集。
利用这两条定律,可以过滤掉很多的候选项集
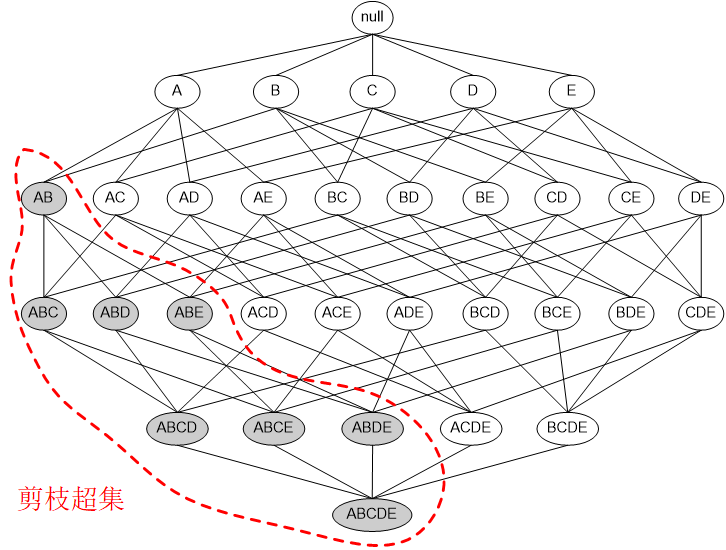
利用性质1通过已知的频繁项集构成长度更大的项集,并将其称为候选频繁项集。
利用性质2过滤候选频繁项集中的非频繁项集
二项频繁集由在一项频繁集的基础上产生的,三项频繁项集由二项频繁项集的基础上产生的,以
此类推。

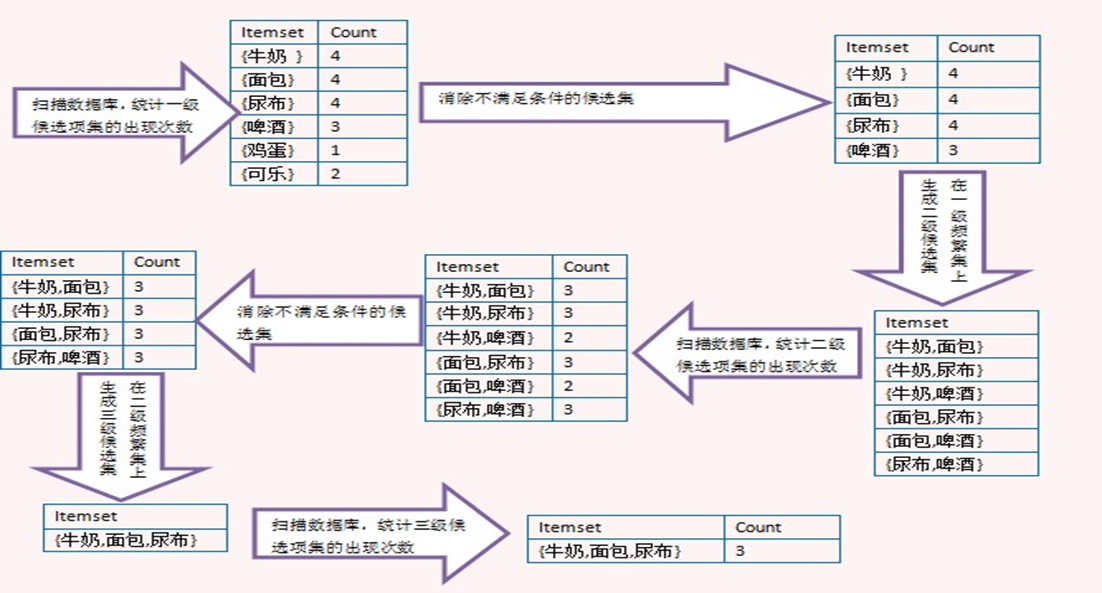
上面的图演示了Apriori算法的过程,注意看由二级频繁项集生成三级候选项集时,没有{牛奶,面包,啤酒},那是因为{面包,啤酒}不是二级频繁项集,这里利用了Apriori定理。
最后生成三级频繁项集后,没有更高一级的候选项集,因此整个算法结束,{牛奶,面包,尿布}是最大频繁子集。
计算菜品间的关联度
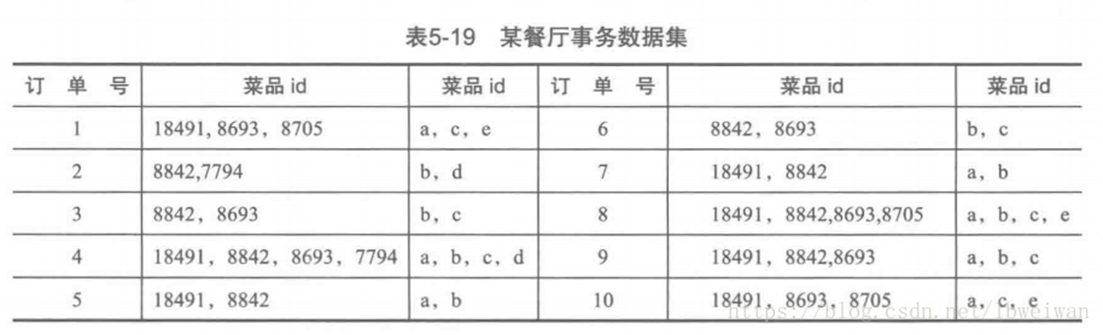
首先计算出所有的频繁项集,这里最小支持度为0.2
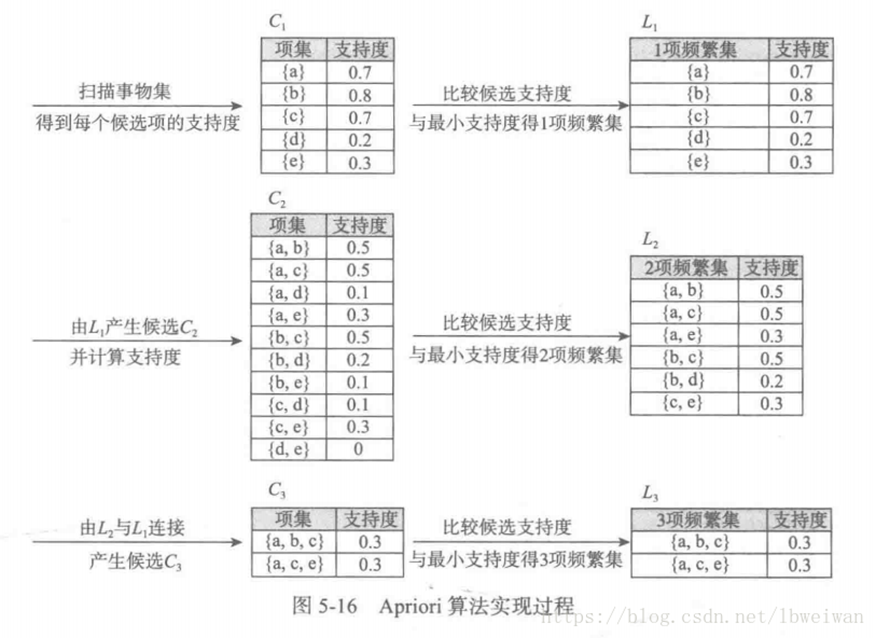
得出L1、L2、L3的各个项集均为频繁项集,再进行计算每个频繁项集的置信度,其中L1不必计算。计算结果如下

Apriori算法不足
可能产生大量的候选集,以及可能需要重复扫描数据库,是Apriori算法的两大缺点。
主要改进方向:
减少候选集产生
降低无效的扫描库次数
提高候选集与原数据的比较效率
Ck中的每个元素需在交易数据库中进行验证来决定其是否加入Lk,这里的验证过程是算法性能的一个瓶颈。这个方法要求多次扫描可能很大的交易数据库,即如果频集最多包含10个项,那么就需要扫描交易数据库10遍,这需要很大的I/O负载。
1.一个项集是频集当且仅当它的所有子集都是频集。那么,如果Ck中某个候选项集有一个(k-1)-子集不属于Lk-1,则这个项集可以被修剪掉不再被考虑,这个修剪过程可以降低计算所有的候选集的支持度的代价。
2.扫描数据库只为了为候选集计数,但一些行比候选集长度还短,再比较就没必要。
3.利用一些hash位图等技术加速原始数据行与候选集的比较功能
FP-Growth算法
相对Apriori算法的改进
Han等人提出FP-Growth(频繁模式增长)算法,通过把交易集D中的信息压缩到一个树结构中,可以在寻找频繁集的过程中不需要产生候选集,大大减少了扫描全库的次数,从而大大提高了运算效率。
FP-TRee
FP-Tree(频繁模式树)是一个树形结构,包括一个频繁项组成的头表,一个标记为null的根结点,它的子结点为一个项前缀子树的集合。
频繁项
单个项目的支持度超过最小支持度则称其为频繁项(frequentitem)
频繁头表
频繁项头表的每个表项由两个域组成,一个是项目名称,一个是链表指针,指向下一个相同项目名称的结点。
生成FP-Growth树
1、遍历数据集,统计各元素项出现次数,创建头指针表
2、移除头指针表中不满足最小值尺度的元素项
3、第二次遍历数据集,创建FP树。对每个数据集中的项集:
3.1初始化空FP树
3.2对每个项集进行过滤和重排序
3.3使用这个项集更新FP树,从FP树的根节点开始:
3.3.1如果当前项集的第一个元素项存在于FP树当前节点的子节点中,则更新这个子节点的计数值
3.3.2否则,创建新的子节点,更新头指针表
3.3.3对当前项集的其余元素项和当前元素项的对应子节点递归3.3的过程
FP-Growth算法更进一步,通过将交易数据巧妙的构建出一颗FP树,然后在FP树中递归的对频繁项进行挖掘。
FP-Growth算法仅仅需要两次扫描数据库,第一次是统计每个商品的频次,用于剔除不满足最低支持度的商品,然后排序得到FreqItems。第二次,扫描数据库构建FP树。
构建频繁项集
| id |
购买的商品 |
| 1 |
a b d |
| 2 |
b c d |
| 3 |
a b e |
| 4 |
a b c |
| 5 |
b c d |
第一步,扫描数据库,统计每个商品的频次,并进行排序,显然商品e仅仅出现了一次,不符合minSupport,剔除。最终得到的结果如下表:
| 商品 |
频次 |
| b |
5 |
| a |
3 |
| c |
3 |
| d |
3 |
构建FP树
第二步,扫描数据库,进行FP树的构建。FP树以root节点为起始,节点包含自身的item和count,以及父节点和子节点。
首先是第一条交易数据,a b d,结合第一步商品顺序,排序后为b a d,依次在树中添加节点b,父节点为root,最新的的频次为1,然后节点a,父节点为a,频次为1,最后节点d,父节点为b,频次为1。
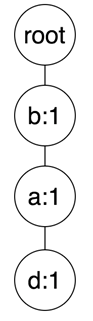
构建FP树
第二条交易数据,排序后为:b c d。依次添加b,树中已经有节点b,因此更新频次加1,然后是节点c,b节点当前只有子节点d,因此新建节点c,父节点为b,频次为1,最后是d,父节点为c,频次为1。
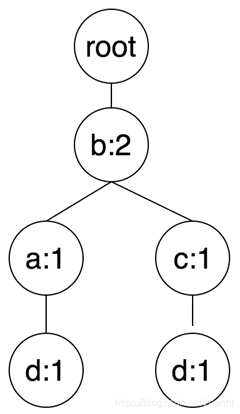
构建FP树
后面三条交易数据的处理和前两条一样
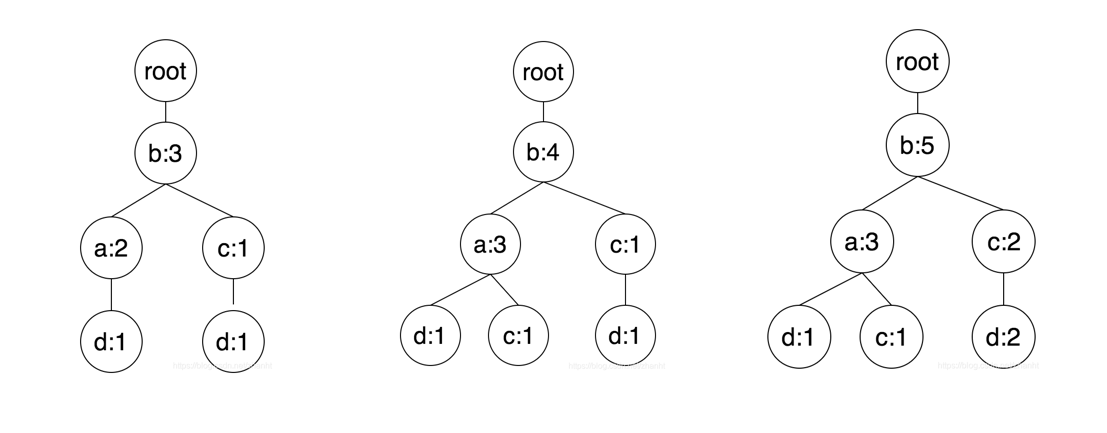
频繁项的挖掘
商品b频繁项的挖掘
首先是商品b,首先b节点本身的频次符合minSupport,所以是一个频繁项(b : 5),然后b节点往上找subTree,只有根节点,所以解锁,b为前缀的频繁项只有一个:(b : 5)。
商品a频繁项的挖掘
a本身是个频繁项(a : 3),然后递归的获取a的子树,进行挖掘。
然后遍历树中所有的a节点,往上找,直到root节点,每个节点的频次为当前遍历节点的频次。因为a只有一个节点(a, 3),所以往上遍历得到节点b,频次为节点(a, 3)的频次3。只能挖掘出频繁项(b : 3),然后这是a递归得到的子树,拼上前缀a,所以得到频繁项为(ab : 3),因此商品a的频繁项挖掘结束,有两个频繁项为:(a : 3), (ab : 3)
商品c频繁项的挖掘商品
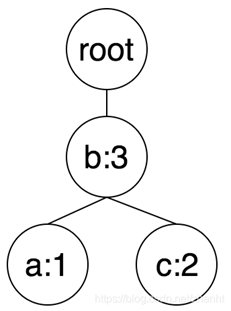
c在FP树中包含两个节点,分别为: (c, 1), (c, 2)。显然c自身是个频繁项(c : 3),然后进行递归。(c, 1)节点往上路径得到如下节点:(a, 1), (b, 1)。节点(c, 2)往上得到(b, 2)。
节点(b, 3)符合minsupport,拼上前缀c得到频繁项(bc : 3)。节点(a, 1)不满足要求,丢弃。
因此,c挖掘出的频繁项为:(c:3), (cb : 3)
![]()
商品d频繁项的挖掘
同理,(d : 3)是一个频繁项,子树首先挖出(c : 2),(b : 3),拼上前缀d得到(dc : 2),(db : 3),然后节点c的仅仅有根节点和节点(b, 2),拼上两个前缀得到(dcb : 2)
最终结果
通过上述的挖掘过程,我们依次挖出了如下9个频繁项:(b : 5), (a : 3), (ab : 3), (c:3), (cb : 3), (d : 3), (dc : 2),(db : 3), (dcb : 2)
总结:
FP-Growth算法 采取如下分治策略:将提供频繁项集的数据库压缩到一棵频繁模式树(FP-tree),但仍保留项集关联信息。减少重复遍历数据的次数,加速计算过程。
关联规则兴趣度
Apriori算法大多是在提升挖掘的效率,而对挖掘出来的规则是否是用户有用,或者说用户感兴趣却研究不多。
现有的许多关联规则发现方法具有以下缺陷:
产生大量的规则,而其中的大部分是显而易见的或不相关的;
没有充分利用管理者的领域知识和职业直觉。管理者的职业直觉往往对知识发现的过程具有重大的价值;
没有提供好的能够评价规则兴趣度的方法。
如何从关联规则中选择出用户最希望得到的知识?
寻找置信度度量的替代物(如兴趣度、有效度、匹配度等)
扩展原有的固定支持度阈值限制的客观评价方法的改进
判断一条关联规则是否有趣可以由两类评价方法:客观兴趣度和主观兴趣度。客观兴趣度主要根据模式或规则的形式和数据库中的数据进行定义,属于数据驱动。主观兴趣度还要考虑客户的参与等人为因索的影响,属于客户驱动。
关联规则挖掘使用支持度-置信度框架存在问题。会产生大量冗余规则。
例如{A,B,C}->{D}等同于{A,B}->{D}强规则不代表有意义,甚至可能误导。
例如conf({怀孕->女性})=100%。
置信度可以看成是在交易数据库中前件发生的 条件下后件概率 P(Y|X )的估计 ,置信度表示某 些项 目集的出现会导致其他项 目集的出现。
置信度作为度量有一个缺点 ,就是只考虑了与的关系,而忽略 了 P(Y) (X=>Y 不等于Y=>X)。例如 :P(XY)/P(X) 的值 可以等于 P(Y) (即 Y出现与X无关--全概率公式 ),但又超过置信度的阀值 可以使规则成立。
关联规则的可信度支持度阈值不能够显示否定示例的情况.
例如, 我们无法采掘出一条规则表示“买了咖啡的顾客不会买奶粉的可能性是34% , 且在交易记录中有46% 的记录是买了咖啡而没买奶粉”. 显然, 这种购买趋势(即买了咖啡不买奶粉) 在现实生活中是很有可能存在的。
买了咖啡同时又卖茶的比较多,但是买了咖啡但是没买茶的更多。造成这种情况的主要问题是2端的数据规模不匹配,买咖啡的人远多余买茶的人,且很多人只买了咖啡。
兴趣度反映 了是X条件下 Y出现的概率与不 考虑X条件下 Y出现的概率比值 ,反映项集X和项 集 y之间的关系。
兴趣度的取值范围为[0,+∞]。当兴趣度等于 1时 ,表明X和 Y同时出现属于概率事件 ,不具有特别意义 ,即X的出现与Y的出现是独立的,互不受影响 ,称该规则为不相关规则
兴趣度小于 1时表明项集X的出现降低了另一个项集 Y出现的可能性 , 称为负相关规则 ;
兴趣度大于 1时表明项集Y在项集出现X的条件下 比在无条件下出现 可能性要大,也就是项集X的出现会带动另一个项集 Y的出 现 ,称为正相关规则。
一般情况下 ,挖掘出正相关 的关联规则更具现 实意义 ,但有时负相关规则 的出现也会 为用户带来新的知识。
这里所说的在上一篇文章中也详细的解释了!
apriori代码案例
# 安装mlxtend : pip install mlxtend
import pandas as pd
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori,fpgrowth,association_rules
# 1. 获取数据(二维列表) list of lists
data_set = [['l1', 'l2', 'l5'],
['l2', 'l4'],
['l2', 'l3'],
['l1', 'l2', 'l4'],
['l1', 'l3'],
['l2', 'l3'],
['l1', 'l3'],
['l1', 'l2', 'l3', 'l5'],
['l1', 'l2', 'l3']]
# 2. 构造项集bool矩阵(One-Hot数据集)
# 使用事务编码器构造One-hot矩阵
encoder = TransactionEncoder()
onehot_data = encoder.fit_transform(data_set)
df = pd.DataFrame(onehot_data, columns=encoder.columns_) # T-F矩阵
#df = pd.DataFrame(onehot_data.astype('int'), columns=encoder.columns_) # 0-1矩阵
# 2. 生成频繁项集
frequent_itemsets = apriori(df,min_support=0.2, use_colnames=True)
print(frequent_itemsets)
# 3. 生成关联规则
associate_rules = association_rules(frequent_itemsets,metric="confidence",min_threshold=0.6)
print(associate_rules)# coding:utf-8
class treeNode: # 定义树节点类
def __init__(self, nameValue, numOccur, parentNode):
self.name = nameValue
self.count = numOccur
self.nodeLink = None
self.parent = parentNode
self.children = {}
def inc(self, numOccur):
self.count += numOccur
def disp(self, ind=1):
print(' '*ind, self.name, ' ', self.count)
for child in self.children.values():
child.disp(ind+1)
def updateHeader(nodeToTest, targetNode):
while nodeToTest.nodeLink != None:
nodeToTest = nodeToTest.nodeLink
nodeToTest.nodeLink = targetNode
def updateFPtree(items, inTree, headerTable, count):
if items[0] in inTree.children:
# 判断items的第一个结点是否已作为子结点
inTree.children[items[0]].inc(count)
else:
# 创建新的分支
inTree.children[items[0]] = treeNode(items[0], count, inTree)
if headerTable[items[0]][1] == None:
headerTable[items[0]][1] = inTree.children[items[0]]
else:
updateHeader(headerTable[items[0]][1], inTree.children[items[0]])
# 递归
if len(items) > 1:
updateFPtree(items[1::], inTree.children[items[0]], headerTable, count)
def createFPtree(dataSet, minSup=1):
headerTable = {}
for trans in dataSet:
for item in trans:
headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
for k in list(headerTable.keys()):
if headerTable[k] < minSup:
del(headerTable[k]) # 删除不满足最小支持度的元素
freqItemSet = set(headerTable.keys()) # 满足最小支持度的频繁项集
if len(freqItemSet) == 0:
return None, None
for k in headerTable:
headerTable[k] = [headerTable[k], None] # element: [count, node]
retTree = treeNode('Null Set', 1, None)
for tranSet, count in dataSet.items():
# dataSet:[element, count]
localD = {}
for item in tranSet:
if item in freqItemSet: # 过滤,只取该样本中满足最小支持度的频繁项
localD[item] = headerTable[item][0] # element : count
if len(localD) > 0:
# 根据全局频数从大到小对单样本排序
# orderedItem = [v[0] for v in sorted(localD.iteritems(), key=lambda p:(p[1], -ord(p[0])), reverse=True)]
orderedItem = [v[0] for v in sorted(localD.items(), key=lambda p:(p[0], int(p[1])), reverse=True)]
# 用过滤且排序后的样本更新树
updateFPtree(orderedItem, retTree, headerTable, count)
return retTree, headerTable
# 回溯
def ascendFPtree(leafNode, prefixPath):
if leafNode.parent != None:
prefixPath.append(leafNode.name)
ascendFPtree(leafNode.parent, prefixPath)
# 条件模式基
def findPrefixPath(basePat, myHeaderTab):
treeNode = myHeaderTab[basePat][1] # basePat在FP树中的第一个结点
condPats = {}
while treeNode != None:
prefixPath = []
ascendFPtree(treeNode, prefixPath) # prefixPath是倒过来的,从treeNode开始到根
if len(prefixPath) > 1:
condPats[frozenset(prefixPath[1:])] = treeNode.count # 关联treeNode的计数
treeNode = treeNode.nodeLink # 下一个basePat结点
return condPats
def mineFPtree(inTree, headerTable, minSup, preFix, freqItemList):
# 最开始的频繁项集是headerTable中的各元素
bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p:p[0])] # 根据频繁项的总频次排序
for basePat in bigL: # 对每个频繁项
newFreqSet = preFix.copy()
newFreqSet.add(basePat)
freqItemList.append(newFreqSet)
condPattBases = findPrefixPath(basePat, headerTable) # 当前频繁项集的条件模式基
myCondTree, myHead = createFPtree(condPattBases, minSup) # 构造当前频繁项的条件FP树
if myHead != None:
# print 'conditional tree for: ', newFreqSet
# myCondTree.disp(1)
mineFPtree(myCondTree, myHead, minSup, newFreqSet, freqItemList) # 递归挖掘条件FP树
def loadSimpDat():
simDat = [['r','z','h','j','p'],
['z','y','x','w','v','u','t','s'],
['z'],
['r','x','n','o','s'],
['y','r','x','z','q','t','p'],
['y','z','x','e','q','s','t','m']]
return simDat
def createInitSet(dataSet):
retDict={}
for trans in dataSet:
key = frozenset(trans)
if key in retDict:
retDict[frozenset(trans)] += 1
else:
retDict[frozenset(trans)] = 1
return retDict
def calSuppData(headerTable, freqItemList, total):
suppData = {}
for Item in freqItemList:
# 找到最底下的结点
Item = sorted(Item, key=lambda x:headerTable[x][0])
base = findPrefixPath(Item[0], headerTable)
# 计算支持度
support = 0
for B in base:
if frozenset(Item[1:]).issubset(set(B)):
support += base[B]
# 对于根的儿子,没有条件模式基
if len(base)==0 and len(Item)==1:
support = headerTable[Item[0]][0]
suppData[frozenset(Item)] = support/float(total)
return suppData
def aprioriGen(Lk, k):
retList = []
lenLk = len(Lk)
for i in range(lenLk):
for j in range(i+1, lenLk):
L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2]
L1.sort(); L2.sort()
if L1 == L2:
retList.append(Lk[i] | Lk[j])
return retList
def calcConf(freqSet, H, supportData, br1, minConf=0.7):
prunedH = []
for conseq in H:
conf = supportData[freqSet] / supportData[freqSet - conseq]
if conf >= minConf:
print("{0} --> {1} conf:{2}".format(freqSet - conseq, conseq, conf))
br1.append((freqSet - conseq, conseq, conf))
prunedH.append(conseq)
return prunedH
def rulesFromConseq(freqSet, H, supportData, br1, minConf=0.7):
m = len(H[0])
if len(freqSet) > m+1:
Hmp1 = aprioriGen(H, m+1)
Hmp1 = calcConf(freqSet, Hmp1, supportData, br1, minConf)
if len(Hmp1)>1:
rulesFromConseq(freqSet, Hmp1, supportData, br1, minConf)
def generateRules(freqItemList, supportData, minConf=0.7):
bigRuleList = []
for freqSet in freqItemList:
H1 = [frozenset([item]) for item in freqSet]
if len(freqSet)>1:
rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
else:
calcConf(freqSet, H1, supportData, bigRuleList, minConf)
return bigRuleListfpgrowth代码案例
import fpgrowth
import time
'''simple data'''
simDat = fpgrowth.loadSimpDat()
initSet = fpgrowth.createInitSet(simDat)
myFPtree, myHeaderTab = fpgrowth.createFPtree(initSet, 3)
myFPtree.disp()
print(fpgrowth.findPrefixPath('z', myHeaderTab))
print(fpgrowth.findPrefixPath('r', myHeaderTab))
print(fpgrowth.findPrefixPath('t', myHeaderTab))
freqItems = []
fpgrowth.mineFPtree(myFPtree, myHeaderTab, 3, set([]), freqItems)
for x in freqItems:
print(x)
# compute support values of freqItems
suppData = fpgrowth.calSuppData(myHeaderTab, freqItems, len(simDat))
suppData[frozenset([])] = 1.0
for x,v in suppData.items():
print(x,v)
freqItems = [frozenset(x) for x in freqItems]
fpgrowth.generateRules(freqItems, suppData)结果
Null Set 1
z 5
r 1
y 3
x 3
t 3
s 2
r 1
x 1
s 1
r 1
{}
{'r'}
{'s'}
{'x', 's'}
{'t'}
{'x', 't'}
{'y', 'x', 't'}
{'y', 'z', 'x', 't'}
{'z', 'x', 't'}
{'y', 't'}
{'y', 'z', 't'}
{'z', 't'}
{'x'}
{'y', 'x'}
{'y', 'z', 'x'}
{'z', 'x'}
{'y'}
{'y', 'z'}
{'z'}
frozenset({'r'}) 0.5
frozenset({'s'}) 0.5
frozenset({'x', 's'}) 0.5
frozenset({'t'}) 0.5
frozenset({'x', 't'}) 0.5
frozenset({'y', 'x', 't'}) 0.0
frozenset({'y', 'z', 'x', 't'}) 0.0
frozenset({'z', 'x', 't'}) 0.5
frozenset({'y', 't'}) 0.0
frozenset({'y', 'z', 't'}) 0.0
frozenset({'z', 't'}) 0.5
frozenset({'x'}) 0.5
frozenset({'y', 'x'}) 0.0
frozenset({'y', 'z', 'x'}) 0.0
frozenset({'z', 'x'}) 0.5
frozenset({'y'}) 0.5
frozenset({'y', 'z'}) 0.5
frozenset({'z'}) 0.8333333333333334
frozenset() 1.0
每文一语
加油!
文章来源: wxw-123.blog.csdn.net,作者:王小王-123,版权归原作者所有,如需转载,请联系作者。
原文链接:wxw-123.blog.csdn.net/article/details/124065993
- 点赞
- 收藏
- 关注作者


评论(0)