1 主要内容

主要内容：
• 决策树学习算法
信息增益
ID3、C4.5、CART
• Bagging与随机森林的思想
投票机制
• 分类算法的评价指标
ROC曲线和AUC值

2 决策树学习的生成算法

• 建立决策树的关键，即在当前状态下选择哪个属性作为分类依据。
• 根据不同的目标函数，建立决策树主要有一下三种
算法。
• ID3
• C4.5
• CART

信息增益

• 概念：当熵和条件熵中的概率由数据估计(特别是极大似然估计)得到时，所对应的熵和条件熵分别称为经验熵和经验条件熵。
• 信息增益表示得知特征A的信息而使得类X的信息的不确定性减少的程度。
• 定义：特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即：
• g(D,A)=H(D) – H(D|A)
• 显然，这即为训练数据集D和特征A的互信息。

三种决策树学习算法

适应信息增益来进行特征选择的决策树学习过程，即为ID3决策。
• 所以如果是取值更多的属性，更容易使得数据更“纯” ，其信息增益更大，决策树会首先挑选这个属性作为树的顶点。结果训练出来的形状是一棵庞大且深度很浅的树，这样的划分是极为不合理的。
• C4.5：信息增益率 gr(D,A) = g(D,A) / H(A)
• CART：基尼指数
• 总结：一个属性的信息增益越大，表明属性对样本的熵减少的能力更强，这个属性使得数据由不确定性变成确定性的能力越强。

决策树的过拟合

• 决策树对训练属于有很好的分类能力，但对未知的测试数据未必有好的分类能力，泛化能力弱，即可能发生过拟合现象。
• 随机森林

3随机森林前言（random forest）

• 随机森林依赖的思想：
• Bootstrap
• Bagging
• 决策树

Bootstraping

Bootstraping的名称来自成语“pull up by your own bootstraps”，意思是依靠你自己的资源，称为自助法，它是一种有放回的抽样方法。

Bagging的策略
• bootstrap aggregation
• 从样本集中重采样(有重复的)选出n个样本
• 在所有属性上，对这n个样本建立分类器(ID3、C4.5、CART、SVM、Logistic回归等) • 重复以上两步m次，即获得了m个分类器
• 将数据放在这m个分类器上，最后根据这m个分类器的投票结果，决定数据属于哪一类

4 随机森林

• 随机森林顾名思义，是用随机的方式建立一个森林，森林里面有很多的决策树组成，随机森林的每一棵决策树之间是没有关联的。
• 在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一棵决策树分别进行一下判断，看看这个样本应该属于哪一类（对于分类算法）；
• 然后看看哪一类被选择最多，就预测这个样本为那一类。
• 随机森林中的“随机”具有两个随机性。
• 两个随机性的引入对随机森林的分类性能至关重要。由于它们的引入，使得随机森林不容易陷入过拟合，并且具有很好得抗噪能力

1 如果训练集大小为N，对于每棵树而言，随机且有放回地从训练集中的抽取N个训
练样本（这种采样方式称为bootstrap sample方法），作为该树的训练集；
• 每棵树的训练集都是不同的，而且里面包，含重复的训练样本（这点很重要。

2 如果每个样本的特征维度为M，指定一个常数m<<M，随机地从M个特征中选取m个特征子集，每次树进行分裂时，从这M个特征中选择最优的；
• 每个节点都将随机选择m(m<M)个特定的变量，然后运用这m个变量来确定最佳的分裂点。在决策树的生成过程中，m的值是保持不变的；
• Typically m = sqrt§ or log§, where p is the number offeatures

3每棵树都尽最大程度的生长，并且没有剪枝过程。

4 通过对所有的决策树进行加总来预测新的数据（在分类时采用多数
投票，在回归时采用平均）

• 随机森林在bagging基础上做了修改。
• 从样本集中用Bootstrap采样选出n个样本；
• 从所有属性中随机选择k个属性，选择最佳分割属性作为节点建立决策树； • 重复以上两步m次，即建立了m棵决策树
• 这m个决策树形成随机森林，通过投票表决结果，决定数据属于哪一类

随机森林/Bagging和决策树的关系
当然可以使用决策树作为基本分类器
• 但也可以使用SVM、Logistic回归等其他分类器，习惯上，这些分类器组成的“总分类器”，仍然叫做随机森林。

离散点是样本集合，描述了臭氧(横轴)和温度(纵轴)的关系
• 试拟合二者的变化曲线

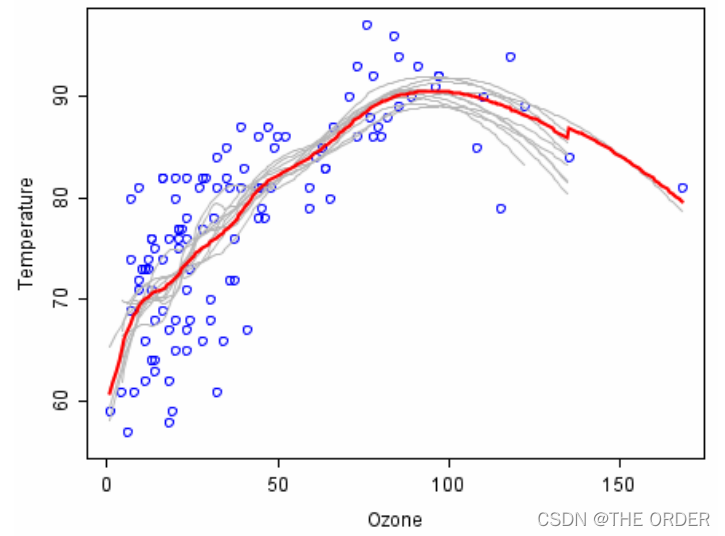
使用Bagging
算法过程

• 做100次bootstrap，每次得到的数据Di，Di的长度为N• 对于每一个Di，使用局部回归(LOESS)拟合一条曲线(图中灰色线是其中的10条曲线) • 将这些曲线取平均，即得到红色的最终拟合曲线

• 显然，红色的曲线更加稳定，并且没有过拟合明显减弱

随机森林、决策树应用

• 决策树R实现
• 最简单package rpart rpart.plot，还有其他如tree、C50等 • 利用R 自带数据iris实现分类

将在下一章节讲解R实现决策树，敬请关注