在 Python 中绘制 Mandelbrot 集
目录
本教程将引导您完成一个有趣的项目,其中涉及Python 中的复数。您将通过使用 Python 的 Matplotlib 和 Pillow 库绘制Mandelbrot 集来了解分形并创建一些真正令人惊叹的艺术。在此过程中,您将了解这个著名的分形是如何被发现的、它代表什么以及它与其他分形的关系。
了解面向对象的编程原理和递归将使您能够充分利用 Python 的表达性语法来编写读起来几乎像数学公式一样的干净代码。要了解制作分形的算法细节,您还应该熟悉复数、对数、集合论和迭代函数。但是不要让这些先决条件吓跑你,因为无论如何你都可以跟随并制作艺术!
在本教程中,您将学习如何:
- 将复数应用于实际问题
- 查找Mandelbrot和Julia集的成员
- 使用Matplotlib和Pillow将这些集合绘制为分形
- 对分形进行丰富多彩的艺术表现
了解曼德布罗集
在您尝试绘制分形之前,这将有助于了解相应的 Mandelbrot 集代表什么以及如何确定其成员。如果您已经熟悉基本理论,请随时跳到下面的绘图部分。
分形几何的标志
即使这个名字对你来说是新的,你也可能以前看过一些令人着迷的 Mandelbrot 集的可视化。它是一组复数,其边界在复平面上描绘时形成独特而复杂的图案。这种模式可以说是最著名的分形,在 20 世纪后期催生了分形几何:

Mandelbrot 集(来源:维基媒体,由 Wolfgang Beyer 创建,CC BY-SA 3.0)
由于技术进步,Mandelbrot 集的发现成为可能。它归功于一位名叫Benoît Mandelbrot的数学家。他在 IBM 工作,可以使用一台能够进行当时要求很高的数字运算的计算机。今天,您可以在舒适的家中探索分形,只使用 Python!
分形是在不同尺度上无限重复的图案。几个世纪以来,哲学家们一直在争论无穷大的存在,但分形确实在现实世界中有一个类比。这是自然界中相当普遍的现象。例如,这种罗马花椰菜是有限的,但具有自相似结构,因为蔬菜的每个部分看起来都像整体,只是更小:

罗马花椰菜的分形结构
自相似性通常可以用递归在数学上定义。Mandelbrot 集并不是完全自相似的,因为它包含在较小尺度上略有不同的自身副本。尽管如此,它仍然可以用复域中的递归函数来描述。
迭代稳定性的边界
形式上,Mandelbrot 集是复数的集合c,其中无限的数字序列z 0 , z 1 , ..., z n , ... 保持有界。换句话说,该序列中每个复数的大小永远不会超过一个限制。Mandelbrot 序列由以下递归公式给出:
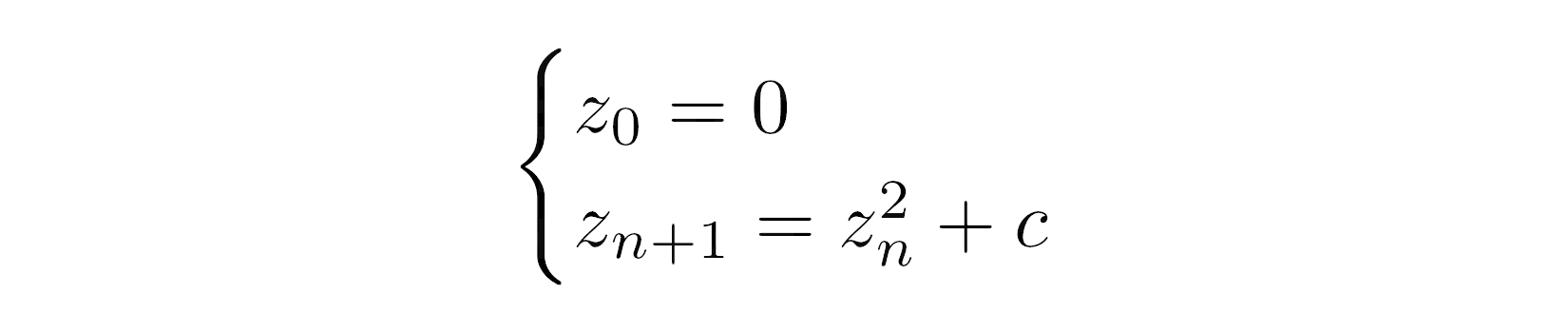
用简单的英语来说,要确定某个复数c是否属于 Mandelbrot 集,您必须将该数字输入到上面的公式中。从现在开始,数字c将在您迭代序列时保持不变。序列的第一个元素z 0始终为零。要计算下一个元素z n+1,您将继续对最后一个元素z n进行平方,并在反馈循环中添加初始数字c 。
通过观察生成的数字序列的行为方式,您将能够将复数c分类为 Mandelbrot 集成员或非 Mandelbrot 集成员。序列是无限的,但您必须在某个时刻停止计算它的元素。做出这样的选择有点武断,取决于您接受的置信水平,因为更多的元素将对c提供更准确的裁决。
注意:当在复平面上描绘时,整个 Mandelbrot 集适合半径为 2 的圆。这是一个方便的事实,可以让您跳过许多不必要的计算,这些计算肯定不属于该集合。
对于复数,您可以在二维中直观地想象这个迭代过程,但现在为了简单起见,您可以继续只考虑实数。如果你要在 Python 中实现上面的等式,那么它可能看起来像这样:
>>> def z(n, c):
... if n == 0:
... return 0
... else:
... return z(n - 1, c) ** 2 + c
您的z()函数返回序列的第 n 个元素,这就是为什么它需要一个元素的索引n, 作为第一个参数。第二个参数c是您正在测试的固定数字。由于递归,这个函数会无限地调用自己。然而,为了打破这个递归调用链,一个条件会使用一个立即已知的解决方案(零)检查基本情况。
尝试使用新函数查找c = 1 序列的前十个元素,看看会发生什么:
>>> for n in range(10):
... print(f"z({n}) = {z(n, c=1)}")
...
z(0) = 0
z(1) = 1
z(2) = 2
z(3) = 5
z(4) = 26
z(5) = 677
z(6) = 458330
z(7) = 210066388901
z(8) = 44127887745906175987802
z(9) = 1947270476915296449559703445493848930452791205
注意这些序列元素的快速增长。它告诉你一些关于c = 1 的成员的信息。具体来说,它不属于Mandelbrot 集,因为相应的序列无限增长。
有时,迭代方法可能比递归方法更有效。这是为指定输入值创建无限序列的等效函数c:
>>> def sequence(c):
... z = 0
... while True:
... yield z
... z = z ** 2 + c
该sequence()函数返回一个生成器对象,在循环中无限地产生序列的连续元素。因为它不返回相应的元素索引,所以您可以枚举它们并在给定次数的迭代后停止循环:
>>> for n, z in enumerate(sequence(c=1)):
... print(f"z({n}) = {z}")
... if n >= 9:
... break
...
z(0) = 0
z(1) = 1
z(2) = 2
z(3) = 5
z(4) = 26
z(5) = 677
z(6) = 458330
z(7) = 210066388901
z(8) = 44127887745906175987802
z(9) = 1947270476915296449559703445493848930452791205
结果和以前一样,但是生成器函数可以让您通过使用惰性求值更有效地计算序列元素。除此之外,迭代消除了对已经计算的序列元素的冗余函数调用。因此,您不再冒达到最大递归限制的风险。
大多数数字会使这个序列发散到无穷大。但是,有些人会通过将序列收敛到单个值或保持在有界范围内来保持稳定。其他人将通过在相同的几个值之间来回循环来使序列周期性地稳定。稳定值和周期性稳定值构成了 Mandelbrot 集。
例如,插入c = 1 会使序列像您刚刚学到的那样无限制地增长,但是c = -1 会导致它在 0 和 -1 之间反复跳跃,而c = 0 会给出由单个值组成的序列:
| 元素 | c = -1 | c = 0 | c = 1 |
|---|---|---|---|
| z 0 | 0 | 0 | 0 |
| z1 | -1 | 0 | 1 |
| z 2 | 0 | 0 | 2 |
| z 3 | -1 | 0 | 5 |
| z 4 | 0 | 0 | 26 |
| z 5 | -1 | 0 | 677 |
| z 6 | 0 | 0 | 458,330 |
| z 7 | -1 | 0 | 210,066,388,901 |
哪些数字是稳定的,哪些不是,这并不明显,因为该公式即使对测试值c的最小变化也很敏感。如果您在复平面上标记稳定数,您将看到以下模式出现:
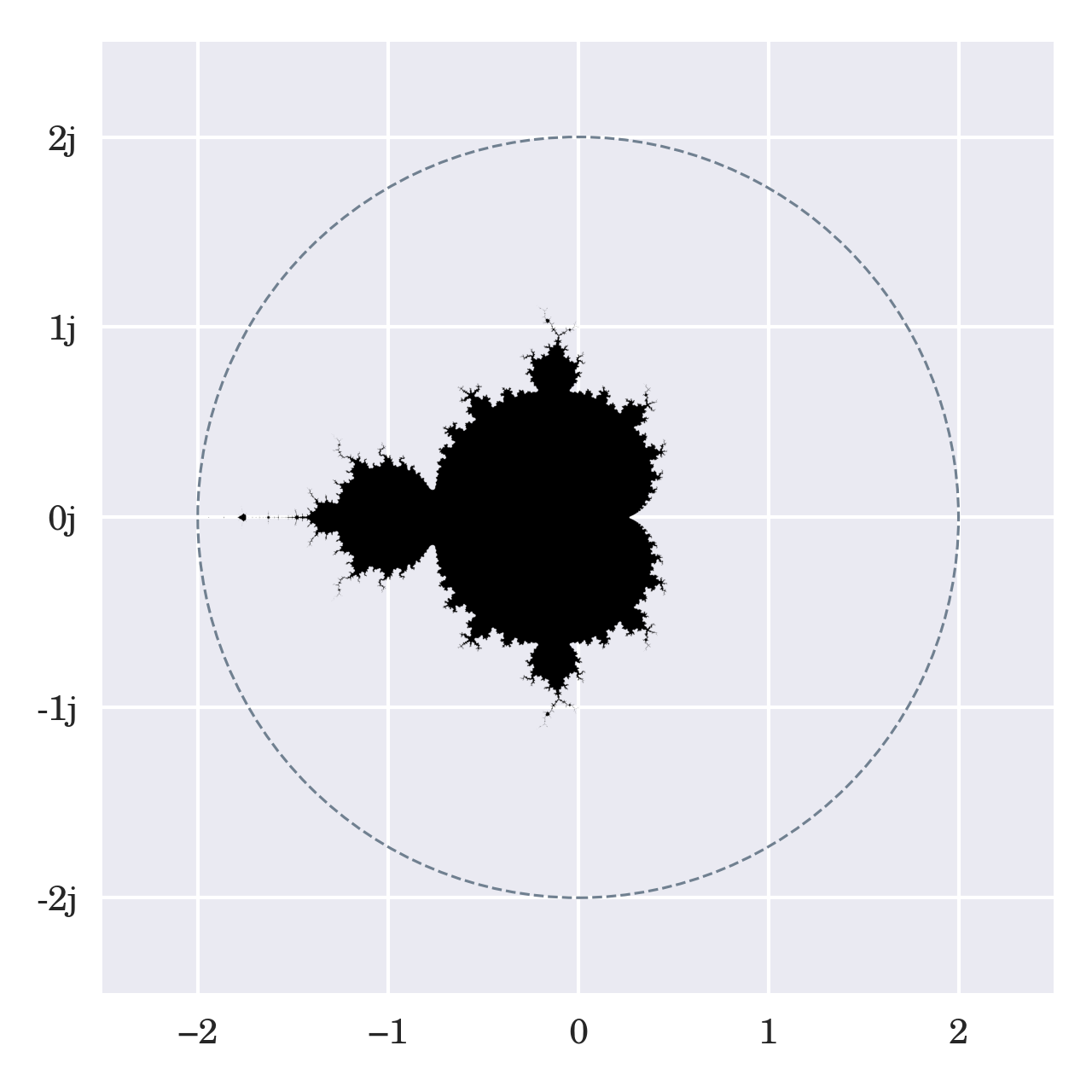
复平面上 Mandelbrot 集的描述
该图像是通过对每个像素运行多达 20 次递归公式生成的,每个像素代表某个c值。当在所有迭代后得到的复数的大小仍然相当小,则相应的像素被着色为黑色。但是,一旦幅度超过半径二,迭代就会停止并跳过当前像素。
有趣的事实:对应于 Mandelbrot 集的分形具有估计为 1.506484 平方单位的有限区域。数学家还没有确定确切的数字,也不知道它是否合理。另一方面,Mandelbrot 集的周长是无限的。查看海岸线悖论,了解现实生活中这个奇怪事实的有趣平行。
您可能会惊讶地发现,一个相对简单的仅涉及加法和乘法的公式可以产生如此精细的结构。但这还不是全部。事实证明,您可以采用相同的公式并使用它来生成无限多个独特的分形!你想看看怎么做吗?
朱莉娅集的地图
如果不提及Julia 集,就很难谈论 Mandelbrot集,这是几十年前法国数学家Gaston Julia在没有计算机帮助的情况下发现的。Julia 集和 Mandelbrot 集密切相关,因为您可以通过相同的递归公式获得它们,只是具有不同的起始条件集。
虽然只有一个 Mandelbrot 集,但有无限多个 Julia 集。到目前为止,您总是从z 0 = 0 开始序列,并系统地测试了某个任意复数c的成员资格。另一方面,要确定一个数字是否属于 Julia 集,您必须使用该数字作为序列的起点,并为c参数选择另一个值。
以下是公式术语的快速比较,具体取决于您正在调查的集合:
| 学期 | 曼德布罗集 | 朱莉娅集 |
|---|---|---|
| z 0 | 0 | 候选值 |
| C | 候选值 | 固定常数 |
在第一种情况下,c代表 Mandelbrot 集的一个潜在成员,并且是唯一需要的输入值,因为z 0保持固定为零。但是,当您在 Julia 模式下使用公式时,每个术语的含义都会发生变化。现在,c用作确定整个 Julia 集的形状和形式的参数,而z 0成为您的兴趣点。与以前不同,Julia 集的公式需要两个输入值而不是一个。
您可以修改之前定义的函数之一,使其更通用。这样,您可以创建从任意点开始的无限序列,而不是始终为零:
def sequence(c, z=0):
while True:
yield z
z = z ** 2 + c
由于突出显示的行中的默认参数值,您仍然可以像以前一样使用此函数,因为z它是可选的。同时,您可以更改序列的起点。在为 Mandelbrot 和 Julia 集定义包装函数之后,您可能会得到一个更好的主意:
def mandelbrot(candidate):
return sequence(z=0, c=candidate)
def julia(candidate, parameter):
return sequence(z=candidate, c=parameter)
每个函数都会返回一个生成器对象,该对象已微调到您想要的起始条件。判断一个候选值是否属于 Julia 集的原理与您之前看到的 Mandelbrot 集相似。简而言之,您必须迭代序列并随着时间的推移观察其行为。
事实上,Benoît Mandelbrot 在他的科学研究中研究 Julia 集。他特别感兴趣的是找到那些产生所谓的连接Julia 集的c值,而不是它们的不连接对应物。后者被称为法头集,当在复平面上可视化时,它表现为由无数个碎片组成的尘埃:
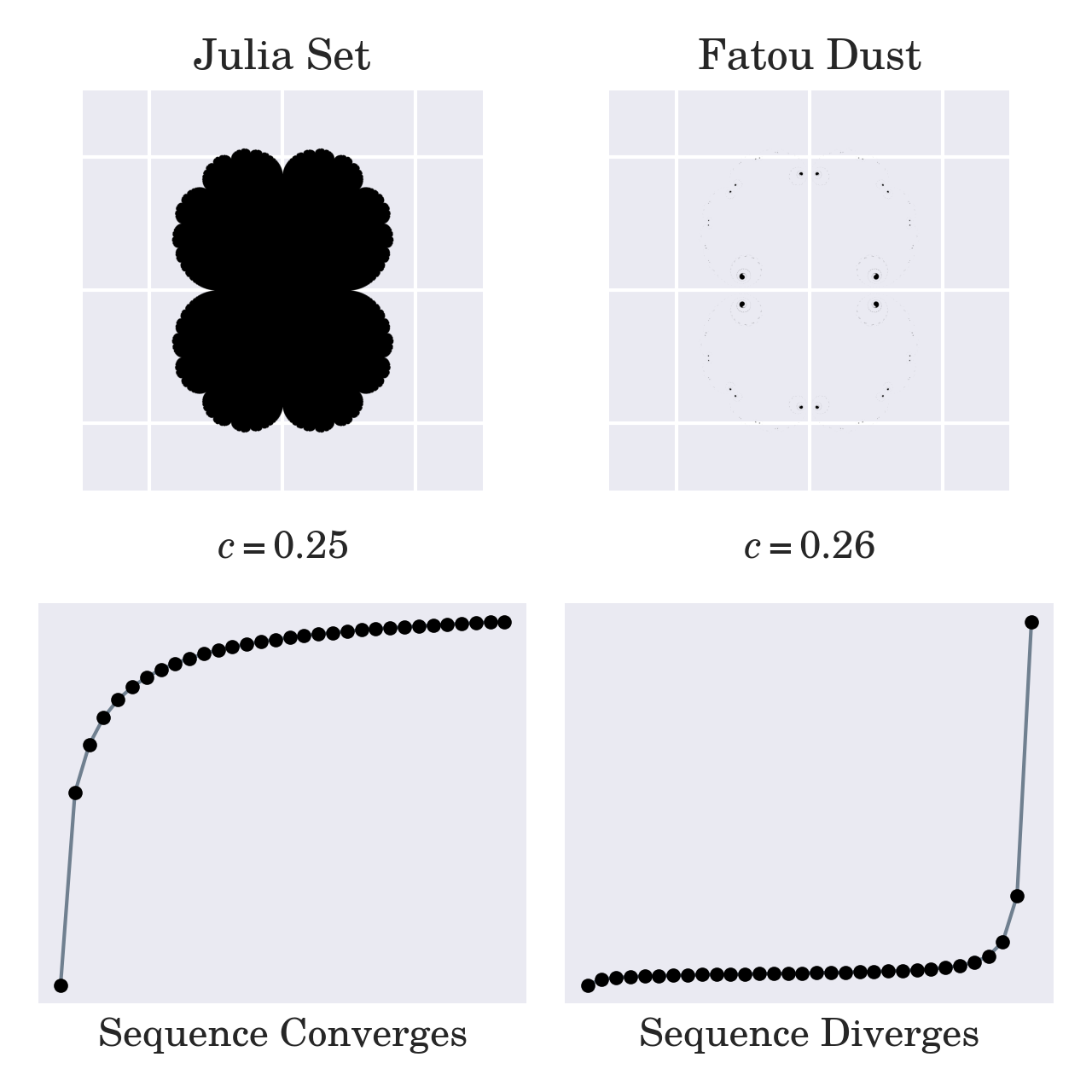
Connected Julia Set vs Fatou Dust
左上角的图像表示从c = 0.25 派生的连接 Julia 集,属于 Mandelbrot 集。您知道将 Mandelbrot 集的一个成员插入递归公式将产生一系列收敛的复数。在这种情况下,数字收敛到 0.5。但是,对c的轻微更改可能会突然将您的 Julia 集变成断开的尘埃,并使相应的序列发散到无穷大。
巧合的是,连接的 Julia 集对应于生成上述递归公式的稳定序列的c值。因此,您可能会说 Benoît Mandelbrot 正在寻找迭代稳定性的边界,或者所有 Julia 集的地图,以显示这些集在哪里连接以及它们在哪里是尘埃。
观察在复平面上为c参数选择不同的点如何影响生成的 Julia 集:
红色的小圆圈表示c的值。只要它停留在左侧所示的 Mandelbrot 集中,右侧描绘的相应 Julia 集就会保持连接。否则,Julia 集会像泡沫一样爆裂,扩散成无数个尘土飞扬的碎片。
你注意到 Julia 集是如何改变形状的吗?事实证明,特定的 Julia 集与用于播种c值的 Mandelbrot 集的特定区域具有共同的视觉特征。当您通过放大镜观察时,两个分形看起来会有些相似。
好了,理论说完了。是时候绘制你的第一个 Mandelbrot 集了!
使用 Python 的 Matplotlib 绘制 Mandelbrot 集
有很多方法可以在 Python 中可视化 Mandelbrot 集。如果您对NumPy和Matplotlib感到满意,那么这两个库将共同提供绘制分形的最直接方法之一。它们方便地使您不必在世界坐标和像素坐标之间进行转换。
注意:世界坐标对应于复平面上的连续数字谱,延伸到无穷大。另一方面,像素坐标是离散的,并且受屏幕有限大小的限制。
要生成初始候选值集,您可以利用np.linspace(),它在给定范围内创建均匀间隔的数字:
1import numpy as np
2
3def complex_matrix(xmin, xmax, ymin, ymax, pixel_density):
4 re = np.linspace(xmin, xmax, int((xmax - xmin) * pixel_density))
5 im = np.linspace(ymin, ymax, int((ymax - ymin) * pixel_density))
6 return re[np.newaxis, :] + im[:, np.newaxis] * 1j
上面的函数将返回一个二维复数数组,该数组包含在由四个参数给定的矩形区域中。xmin和xmax参数指定水平方向的边界,而和ymin指定ymax垂直方向的边界。第五个参数pixel_density确定每单位所需的像素数。
现在,您可以获取该复数矩阵并通过众所周知的递归公式运行它,以查看哪些数字保持稳定,哪些数字保持稳定。由于 NumPy 的矢量化,您可以将矩阵作为单个参数传递c,并在每个元素上执行计算,而无需编写显式循环:
8def is_stable(c, num_iterations):
9 z = 0
10 for _ in range(num_iterations):
11 z = z ** 2 + c
12 return abs(z) <= 2
突出显示行上的代码在每次迭代中针对矩阵的所有元素执行。c因为最初从不同z的c维度开始,NumPy 使用广播巧妙地扩展前者,使两者最终具有兼容的形状。最后,该函数在结果矩阵 上创建布尔值的二维掩码z。每个值对应于该点的序列稳定性。
注意:为了利用向量化计算,代码示例中的循环会无条件地对数字进行平方和相加,无论它们已经有多大。这并不理想,因为在许多情况下,数字很早就发散到无穷大,使得大部分计算都是浪费的。
此外,快速增长的数字通常会导致溢出错误。NumPy 检测到此类溢出并在标准错误流 (stderr)上发出警告。如果您想禁止此类警告,则可以在调用函数之前定义相关过滤器:
1import numpy as np
2
3np.warnings.filterwarnings("ignore")
忽略这些溢出是无害的,因为您对特定幅度不感兴趣,而是对它们是否符合给定阈值感兴趣。
在选定的迭代次数之后,矩阵中每个复数的大小将保持在或超过阈值 2。那些足够小的可能是 Mandelbrot 集的成员。您现在可以使用 Matplotlib 将它们可视化。
低分辨率散点图
可视化 Mandelbrot 集的一种快速而肮脏的方法是通过散点图,它说明了成对变量之间的关系。因为复数是实部和虚部的对,所以您可以将它们解开成单独的数组,这些数组可以很好地与散点图配合使用。
但首先,您需要将布尔稳定性掩码转换为作为序列种子的初始复数。你可以在 NumPy 的掩码过滤的帮助下做到这一点:
16def get_members(c, num_iterations):
17 mask = is_stable(c, num_iterations)
18 return c[mask]
此函数将返回一个一维数组,该数组仅包含那些稳定且因此属于 Mandelbrot 集的复数。当您组合到目前为止定义的函数时,您将能够使用 Matplotlib 显示散点图。不要忘记在文件开头添加必要的导入语句:
1import matplotlib.pyplot as plt
2import numpy as np
3
4np.warnings.filterwarnings("ignore")
这会将绘图界面带到您当前的命名空间。现在您可以计算数据并绘制它:
21c = complex_matrix(-2, 0.5, -1.5, 1.5, pixel_density=21)
22members = get_members(c, num_iterations=20)
23
24plt.scatter(members.real, members.imag, color="black", marker=",", s=1)
25plt.gca().set_aspect("equal")
26plt.axis("off")
27plt.tight_layout()
28plt.show()
调用complex_matrix()准备一个矩形复数数组,在 x 方向的范围为 -2 到 0.5,在 y 方向的范围为 -1.5 到 1.5。随后的调用get_members()仅通过那些属于 Mandelbrot 集的数字。最后,plt.scatter()绘制集合,并plt.show()显示这张图片:

Mandelbrot 集在散点图中的可视化
它包含 749 个点,类似于几十年前 Benoît Mandelbrot 本人在点阵打印机上制作的原始 ASCII 打印输出。你正在重温数学史!通过调整像素密度和迭代次数来观察它们如何影响结果。
高分辨率黑白可视化
要获得更详细的黑白 Mandelbrot 集可视化效果,您可以不断增加散点图的像素密度,直到各个点变得难以辨别。plt.imshow()或者,您可以使用带有二进制颜色图的Matplotlib函数来绘制您的布尔稳定性掩码。
您现有的代码中只需要进行一些调整:
21c = complex_matrix(-2, 0.5, -1.5, 1.5, pixel_density=512)
22plt.imshow(is_stable(c, num_iterations=20), cmap="binary")
23plt.gca().set_aspect("equal")
24plt.axis("off")
25plt.tight_layout()
26plt.show()
将像素密度提高到足够大的值,例如 512。然后,删除对 的调用get_members(),并将散点图替换为plt.imshow()以将数据显示为图像。如果一切顺利,那么您应该会看到这张 Mandelbrot 集的图片:

黑白 Mandelbrot 集的高分辨率可视化
要放大分形的特定区域,请相应地更改复矩阵的边界并将迭代次数增加十倍或更多。您还可以尝试使用 Matplotlib 提供的不同颜色图。然而,要真正释放你内心的艺术家,你可能想用Python 最受欢迎的图像库Pillow让你的脚湿透。
用枕头画曼德布罗套装
本节需要更多的努力,因为您将完成 NumPy 和 Matplotlib 之前为您完成的一些工作。但是,对可视化过程进行更精细的控制将使您能够以更有趣的方式描绘 Mandelbrot 集。在此过程中,您将学习一些有用的概念并遵循最佳Pythonic实践。
NumPy 与 Pillow 一起使用就像与 Matplotlib 一样。np.asarray()您可以使用或以其他方式将 Pillow 图像转换为 NumPy 数组Image.fromarray()。由于这种兼容性,您可以通过将 Matplotlib 替换plt.imshow()为对 Pillow 工厂方法的非常相似的调用来更新上一节中的绘图代码:
21c = complex_matrix(-2, 0.5, -1.5, 1.5, pixel_density=512)
22image = Image.fromarray(~is_stable(c, num_iterations=20))
23image.show()
请注意在稳定性矩阵前面使用按位非运算符( ),它会反转所有布尔值。~这是为了使 Mandelbrot 集在白色背景上显示为黑色,因为 Pillow 默认采用黑色背景。
如果 NumPy 是您熟悉的首选工具,请随时将其整合到本节中。它的执行速度将比您即将看到的纯 Python 代码快得多,因为 NumPy 经过高度优化并依赖于已编译的机器代码。尽管如此,从头开始实现绘图代码将使您能够最终控制并深入了解所涉及的各个步骤。
有趣的事实:Pillow 图像库带有一个方便的函数,可以在一行 Python 代码中生成 Mandelbrot 集的图像:
from PIL import Image
Image.effect_mandelbrot((512, 512), (-3, -2.5, 2, 2.5), 100).show()
传递给函数的第一个参数是一个元组,其中包含生成图像的宽度和高度(以像素为单位)。下一个参数将边界框定义为左下角和右上角。第三个参数是从 0 到 100 的图像质量。
如果您对该函数的工作原理感兴趣,请查看 GitHub 上相应的C 源代码。
在本节的其余部分中,您将自己完成艰苦的工作,而不会走捷径。
寻找集合的收敛元素
之前,您使用 NumPy 的向量化构建了一个稳定性矩阵,以确定给定复数中的哪些属于 Mandelbrot 集。您的函数对公式进行了固定次数的迭代,并返回了一个布尔值的二维数组。使用纯 Python,您可以修改此函数,使其适用于单个数字而不是整个矩阵:
>>> def is_stable(c, max_iterations):
... z = 0
... for _ in range(max_iterations):
... z = z ** 2 + c
... if abs(z) > 2:
... return False
... return True
它看起来与之前的 NumPy 版本非常相似。但是,有一些重要的区别。值得注意的是,c参数表示单个复数,函数返回标量布尔值。其次,循环体中有一个 if 条件,一旦结果数的大小达到已知阈值,它就可以提前终止迭代。
注意:函数参数之一已从 重命名num_iterations为max_iterations以反映迭代次数不再固定并且可以在测试值之间变化的事实。
您可以使用新函数来确定复数是否创建收敛的稳定序列。这直接转化为 Mandelbrot 集合成员。但是,结果可能取决于请求的最大迭代次数:
>>> is_stable(0.26, max_iterations=20)
True
>>> is_stable(0.26, max_iterations=30)
False
例如,数字c = 0.26 位于分形边缘附近,因此如果迭代次数太少,您将得到错误的答案。增加最大迭代次数可以更准确,显示可视化的更多细节。
调用函数并没有错,但使用 Pythonin和not in运算符不是更好吗?将此代码转换为Python 类将允许您覆盖这些运算符并利用更清晰和更 Pythonic 的语法。此外,通过将状态封装在对象中,您将能够在许多函数调用中保留最大迭代次数。
您可以利用数据类来避免必须定义自定义构造函数。这是相同代码的基于类的等效实现:
# mandelbrot.py
from dataclasses import dataclass
@dataclass
class MandelbrotSet:
max_iterations: int
def __contains__(self, c: complex) -> bool:
z = 0
for _ in range(self.max_iterations):
z = z ** 2 + c
if abs(z) > 2:
return False
return True
除了实现特殊方法 .__contains__()、添加一些类型提示以及将max_iterations参数从函数签名中移出之外,其余代码保持不变。假设您将它保存在一个名为 的文件中mandelbrot.py,您可以在同一目录中启动交互式 Python 解释器会话并导入您的类:
>>> from mandelbrot import MandelbrotSet
>>> mandelbrot_set = MandelbrotSet(max_iterations=30)
>>> 0.26 in mandelbrot_set
False
>>> 0.26 not in mandelbrot_set
True
杰出的!这正是您对 Mandelbrot 集进行黑白可视化所需的信息。稍后,您将了解使用 Pillow 绘制像素的一种不那么冗长的方法,但这里是初学者的粗略示例:
>>> from mandelbrot import MandelbrotSet
>>> mandelbrot_set = MandelbrotSet(max_iterations=20)
>>> width, height = 512, 512
>>> scale = 0.0075
>>> BLACK_AND_WHITE = "1"
>>> from PIL import Image
>>> image = Image.new(mode=BLACK_AND_WHITE, size=(width, height))
>>> for y in range(height):
... for x in range(width):
... c = scale * complex(x - width / 2, height / 2 - y)
... image.putpixel((x, y), c not in mandelbrot_set)
...
>>> image.show()
从库中导入Image模块后,您将创建一个具有黑白像素模式和 512 x 512 像素大小的新枕头图像。然后,当您迭代像素行和列时,您将每个点从像素坐标缩放并转换为世界坐标。最后,当对应的复数不属于 Mandelbrot 集时,打开一个像素,使分形的内部保持黑色。
注意:在此特定像素模式下,该.putpixel()方法需要数值为 1 或 0。但是,一旦布尔表达式被评估为上面的代码片段True或False在上面的代码片段中,Python 将分别将其替换为 1 或 0。它按预期工作,因为 Python 的bool数据类型实际上是整数的子类。
当您执行此代码时,您会立即注意到它的运行速度比前面的示例慢得多。如前所述,这部分是因为 NumPy 和 Matplotlib 为高度优化的 C 代码提供了 Python 绑定,而您刚刚在纯 Python 中实现了最关键的部分。除此之外,您还有嵌套循环,并且您正在调用一个函数数十万次!
无论如何,不要担心性能。你的目标是学习在 Python 中绘制 Mandelbrot 集的基础知识。接下来,您将通过在其中显示更多信息来改进分形可视化。
用逃逸计数测量分歧
好的,您知道如何判断一个复数是否使 Mandelbrot 序列收敛,这反过来又可以让您将 Mandelbrot 集可视化为黑色和白色。您可以通过从二值图像到每个像素超过两个强度级别的灰度来增加一点深度吗?答案是肯定的!
尝试从不同的角度看待问题。您可以量化位于 Mandelbrot 集之外的点使递归公式发散到无穷大的速度,而不是找到分形的锐边。有些会很快变得不稳定,而另一些可能需要数十万次迭代才能完成。一般来说,靠近分形边缘的点比远离分形的点不稳定。
通过足够多的迭代,不间断地遍历所有迭代将表明测试的数字很可能是集合成员,因为相关的序列元素保持稳定。另一方面,只有当序列明显发散时,才会在达到最大迭代次数之前跳出循环。检测分歧所需的迭代次数称为逃逸计数。
注意:使用迭代方法测试给定点的稳定性只是实际 Mandelbrot 集的近似值。对于某些点,您需要比最大迭代次数更多的迭代才能知道它们是否稳定,这在实践中可能不可行。
您可以使用转义计数来引入多级灰度。但是,处理归一化转义计数通常更方便,这样无论最大迭代次数如何,它们的值都在从零到一的范围内。要计算给定点的这种稳定性指标,请使用做出决定所需的实际迭代次数与您无条件退出的最大次数之间的比率。
让我们修改您的MandelbrotSet类以计算转义计数。首先,相应地重命名您的特殊方法并使其返回迭代次数而不是布尔值:
# mandelbrot.py
from dataclasses import dataclass
@dataclass
class MandelbrotSet:
max_iterations: int
def escape_count(self, c: complex) -> int:
z = 0
for iteration in range(self.max_iterations):
z = z ** 2 + c
if abs(z) > 2:
return iteration
return self.max_iterations
注意循环如何声明一个变量iteration, 来计算迭代次数。接下来,将稳定性定义为逃逸计数与最大迭代次数的比率:
# mandelbrot.py
from dataclasses import dataclass
@dataclass
class MandelbrotSet:
max_iterations: int
def stability(self, c: complex) -> float:
return self.escape_count(c) / self.max_iterations
def escape_count(self, c: complex) -> int:
z = 0
for iteration in range(self.max_iterations):
z = z ** 2 + c
if abs(z) > 2:
return iteration
return self.max_iterations
最后,带回已删除的特殊方法,成员资格测试操作员in委托给该方法。但是,您将使用建立在稳定性之上的稍微不同的实现:
# mandelbrot.py
from dataclasses import dataclass
@dataclass
class MandelbrotSet:
max_iterations: int
def __contains__(self, c: complex) -> bool:
return self.stability(c) == 1
def stability(self, c: complex) -> float:
return self.escape_count(c) / self.max_iterations
def escape_count(self, c: complex) -> int:
z = 0
for iteration in range(self.max_iterations):
z = z ** 2 + c
if abs(z) > 2:
return iteration
return self.max_iterations
True只有当稳定性等于 1 或 100% 时,成员资格测试算子才会返回。否则,您将获得False价值。您可以通过以下方式检查具体的逃逸计数和稳定性值:
>>> from mandelbrot import MandelbrotSet
>>> mandelbrot_set = MandelbrotSet(max_iterations=30)
>>> mandelbrot_set.escape_count(0.25)
30
>>> mandelbrot_set.stability(0.25)
1.0
>>> 0.25 in mandelbrot_set
True
>>> mandelbrot_set.escape_count(0.26)
29
>>> mandelbrot_set.stability(0.26)
0.9666666666666667
>>> 0.26 in mandelbrot_set
False
对于c = 0.25,观察到的迭代次数与声明的最大迭代次数相同,使稳定性等于 1。相反,选择c = 0.26 会产生略微不同的结果。
该类的更新实现MandelbrotSet允许灰度可视化,它将像素强度与稳定性联系起来。您可以重用上一节中的大部分绘图代码,但您需要将像素模式更改为L,它代表亮度。在这种模式下,每个像素取一个 0 到 255 之间的整数值,因此您还需要适当地缩放分数稳定性:
>>> from mandelbrot import MandelbrotSet
>>> mandelbrot_set = MandelbrotSet(max_iterations=20)
>>> width, height = 512, 512
>>> scale = 0.0075
>>> GRAYSCALE = "L"
>>> from PIL import Image
>>> image = Image.new(mode=GRAYSCALE, size=(width, height))
>>> for y in range(height):
... for x in range(width):
... c = scale * complex(x - width / 2, height / 2 - y)
... instability = 1 - mandelbrot_set.stability(c)
... image.putpixel((x, y), int(instability * 255))
...
>>> image.show()
同样,要在仅照亮其外部的同时将 Mandelbrot 设置为黑色,您必须通过从其中减去它来反转稳定性。当一切按计划进行时,您将看到以下图像的粗略描述:

Pillow 对 Mandelbrot 集的灰度渲染
哇!这看起来已经更有趣了。不幸的是,稳定性值在明显离散的水平上出现量化,因为转义计数是整数。增加最大迭代次数可以帮助缓解这种情况,但仅限于一定程度。此外,添加更多的迭代将过滤掉大量的噪音,在这个放大倍数上留下更少的内容。
在下一小节中,您将了解消除条带伪影的更好方法。
平滑条带伪影
摆脱 Mandelbrot 套装外部的色带归结为使用分数转义计数。插入中间值的一种方法是使用对数。底层数学相当复杂,所以让我们用数学家的话来更新代码:
# mandelbrot.py
from dataclasses import dataclass
from math import log
@dataclass
class MandelbrotSet:
max_iterations: int
escape_radius: float = 2.0
def __contains__(self, c: complex) -> bool:
return self.stability(c) == 1
def stability(self, c: complex, smooth=False) -> float:
return self.escape_count(c, smooth) / self.max_iterations
def escape_count(self, c: complex, smooth=False) -> int | float:
z = 0
for iteration in range(self.max_iterations):
z = z ** 2 + c
if abs(z) > self.escape_radius:
if smooth:
return iteration + 1 - log(log(abs(z))) / log(2)
return iteration
return self.max_iterations
从模块导入log()函数后math,您添加一个可选的布尔标志来控制您的方法的平滑。当您打开平滑时,数学魔法就会通过将迭代次数与发散数的空间信息结合起来,从而产生一个浮点数。
注意:上面的数学公式是基于逃逸半径接近无穷大的假设,所以不能再硬编码了。这就是为什么您的类现在定义了一个默认值为 2 的可选escape_radius字段,您可以在创建MandelbrotSet.
请注意,由于平滑逃逸计数公式中的对数,相关的稳定性可能会过冲甚至变为负数!这是一个简单的示例,可以证明这一点:
>>> from mandelbrot import MandelbrotSet
>>> mandelbrot_set = MandelbrotSet(max_iterations=30)
>>> mandelbrot_set.stability(-1.2039 - 0.1996j, smooth=True)
1.014794475165942
>>> mandelbrot_set.stability(42, smooth=True)
-0.030071301713066417
大于一且小于零的数字将导致像素强度环绕允许的最大和最小级别。所以,不要忘记在点亮一个像素之前和之前钳制你的缩放像素值:max()min()
# mandelbrot.py
from dataclasses import dataclass
from math import log
@dataclass
class MandelbrotSet:
max_iterations: int
escape_radius: float = 2.0
def __contains__(self, c: complex) -> bool:
return self.stability(c) == 1
def stability(self, c: complex, smooth=False, clamp=True) -> float:
value = self.escape_count(c, smooth) / self.max_iterations
return max(0.0, min(value, 1.0)) if clamp else value
def escape_count(self, c: complex, smooth=False) -> int | float:
z = 0
for iteration in range(self.max_iterations):
z = z ** 2 + c
if abs(z) > self.escape_radius:
if smooth:
return iteration + 1 - log(log(abs(z))) / log(2)
return iteration
return self.max_iterations
在计算稳定性时,您默认启用钳位,但让最终用户决定如何处理上溢和下溢。一些色彩丰富的可视化可能会利用这种包装来产生有趣的效果。这由上述方法clamp中的标志控制.stability()。您将在后面的部分中使用可视化。
以下是如何将更新后的MandelbrotSet课程付诸实践:
>>> from mandelbrot import MandelbrotSet
>>> mandelbrot_set = MandelbrotSet(max_iterations=20, escape_radius=1000)
>>> width, height = 512, 512
>>> scale = 0.0075
>>> GRAYSCALE = "L"
>>> from PIL import Image
>>> image = Image.new(mode=GRAYSCALE, size=(width, height))
>>> for y in range(height):
... for x in range(width):
... c = scale * complex(x - width / 2, height / 2 - y)
... instability = 1 - mandelbrot_set.stability(c, smooth=True)
... image.putpixel((x, y), int(instability * 255))
...
>>> image.show()
smooth您可以通过打开用于稳定性计算的标志来启用平滑。但是,仅这样做仍然会产生一点点条带,因此您也可以将逃生半径增加到一个相对较大的值,例如一千。最后,您将看到具有丝般光滑外观的 Mandelbrot 套装图片:

触手可及的部分逃逸计数为在 Mandelbrot 集可视化中使用颜色提供了有趣的可能性。稍后您将探索它们,但首先,您可以改进和简化绘图代码,使其更加健壮和优雅。
在集合元素和像素之间转换
到目前为止,您的可视化已经描绘了分形的静态图像,但它并没有让您放大特定区域或平移以显示更多细节。与之前的对数不同,缩放和转换图像的数学运算并不是非常困难。但是,它增加了一些代码复杂性,值得在继续之前将其抽象为辅助类。
在高层次上,绘制 Mandelbrot 集可以分为三个步骤:
- 将像素的坐标转换为复数。
- 检查该复数是否属于 Mandelbrot 集。
- 根据像素的稳定性为其分配颜色。
您可以构建一个智能像素数据类型,它将封装坐标系之间的转换、考虑缩放和处理颜色。对于 Pillow 和像素之间的集成层,您可以设计一个视口类来处理平移和缩放。
Pixel和类的代码Viewport很快就会出现,但是一旦它们被实现,你就可以用几行 Python 代码重写绘图代码:
>>> from PIL import Image
>>> from mandelbrot import MandelbrotSet
>>> from viewport import Viewport
>>> mandelbrot_set = MandelbrotSet(max_iterations=20)
>>> image = Image.new(mode="1", size=(512, 512), color=1)
>>> for pixel in Viewport(image, center=-0.75, width=3.5):
... if complex(pixel) in mandelbrot_set:
... pixel.color = 0
...
>>> image.show()
而已!该类Viewport包装了枕头图像的一个实例。它根据中心点和世界单位的视口宽度计算出相关的缩放因子、偏移量和世界坐标的垂直范围。作为一个可迭代的,它还提供Pixel可以循环的对象。像素知道如何将自己转换为复数,并且它们是由视口包裹的图像实例的朋友。
注意:传递给枕头图像的构造函数的第三个参数允许您设置背景颜色,默认为黑色。在这种情况下,您需要一个白色背景,它对应于二进制像素模式中等于 1 的像素强度。
您可以通过使用@dataclass装饰器对其进行注释来实现视口,就像MandelbrotSet之前对类所做的那样:
# viewport.py
from dataclasses import dataclass
from PIL import Image
@dataclass
class Viewport:
image: Image.Image
center: complex
width: float
@property
def height(self):
return self.scale * self.image.height
@property
def offset(self):
return self.center + complex(-self.width, self.height) / 2
@property
def scale(self):
return self.width / self.image.width
def __iter__(self):
for y in range(self.image.height):
for x in range(self.image.width):
yield Pixel(self, x, y)
视口将图像实例、表示为复数的中心点和世界坐标的水平范围作为参数。它还从这三个参数中派生了一些只读属性,像素稍后将使用这些属性。最后,该类实现了一个特殊的方法,.__iter__()它是Python 中迭代器协议的一部分,它使得对自定义类的迭代成为可能。
正如您通过查看上面的代码块可能已经猜到的那样,Pixel该类接受Viewport实例和像素坐标:
# viewport.py (continued)
# ...
@dataclass
class Pixel:
viewport: Viewport
x: int
y: int
@property
def color(self):
return self.viewport.image.getpixel((self.x, self.y))
@color.setter
def color(self, value):
self.viewport.image.putpixel((self.x, self.y), value)
def __complex__(self):
return (
complex(self.x, -self.y)
* self.viewport.scale
+ self.viewport.offset
)
这里只定义了一个属性,但它包含像素颜色的 getter 和 setter,它们通过视口委托给 Pillow。特殊方法.__complex__()负责将像素转换为世界单位的相关复数。它沿垂直轴翻转像素坐标,将它们转换为复数,然后利用复数算法来缩放和移动它们。
继续尝试一下您的新代码。Mandelbrot 集包含几乎无限的复杂结构,只有在放大倍率下才能看到。一些地区的特点是螺旋形和曲折形,类似于海马、章鱼或大象。放大时,不要忘记增加最大迭代次数以显示更多细节:
>>> from PIL import Image
>>> from mandelbrot import MandelbrotSet
>>> from viewport import Viewport
>>> mandelbrot_set = MandelbrotSet(max_iterations=256, escape_radius=1000)
>>> image = Image.new(mode="L", size=(512, 512))
>>> for pixel in Viewport(image, center=-0.7435 + 0.1314j, width=0.002):
... c = complex(pixel)
... instability = 1 - mandelbrot_set.stability(c, smooth=True)
... pixel.color = int(instability * 255)
...
>>> image.show()
视口跨越 0.002 个世界单位,以 -0.7435 + 0.1314j 为中心,靠近产生美丽螺旋的Misiurewicz 点。根据迭代次数,您将获得具有不同细节程度的更暗或更亮的图像。如果您愿意,可以使用 Pillow 来增加亮度:
>>> from PIL import ImageEnhance
>>> enhancer = ImageEnhance.Brightness(image)
>>> enhancer.enhance(1.25).show()
这将使图像亮 25% 并显示这个螺旋:

Mandelbrot 集以 Misiurewicz 点为中心
您可以找到更多产生如此壮观结果的独特点。维基百科拥有一个完整的图片库,其中包含值得探索的 Mandelbrot 集的各种细节。
如果您已经开始检查不同的点,那么您可能还注意到渲染时间对您当前正在查看的区域高度敏感。远离分形的像素会更快地发散到无穷大,而靠近分形的像素往往需要更多的迭代。因此,特定区域中的内容越多,解决这些像素是否稳定或不稳定所需的时间就越长。
您可以使用一些选项来提高 Python 中的 Mandelbrot 集渲染性能。但是,它们超出了本教程的范围,因此如果您好奇,请随意探索它们。现在是时候给你的分形一些颜色了。
制作曼德布罗集的艺术表现形式
由于您已经可以绘制灰色阴影的分形,因此添加更多颜色应该不会太困难。如何将像素的稳定性映射到色调完全取决于您。虽然有许多算法可以以美观的方式绘制 Mandelbrot 集,但您的想象力是唯一的限制!
如果您还没有关注,那么您可以通过单击下面的链接下载随附的代码:
在继续之前,您需要对上一节中的绘图代码进行一些调整。具体来说,您将切换到更丰富的颜色模式并定义一些可重用的辅助函数,以使您的生活更轻松。
调色板
自古以来,艺术家们一直在一个叫做调色板的物理板上混合颜料。在计算中,调色板代表一个颜色查找表,它是一种无损压缩形式。它通过索引每种颜色一次然后在所有相关像素中引用它来减少图像的内存占用。
这种技术相对简单且计算速度快。同样,您可以使用预定义的调色板来绘制分形。但是,您可以使用转义计数作为调色板的索引,而不是使用像素坐标来查找相应的颜色。事实上,您早期的可视化已经通过应用 256 种单色灰色的调色板做到了这一点,只是没有将它们缓存在查找表中。
要使用更多颜色,您需要先在RGB 模式下创建图像,这将分配 24 位/像素:
image = Image.new(mode="RGB", size=(width, height))
从现在开始,Pillow 将把每个像素表示为一个由红色、绿色和蓝色 (RGB)颜色通道组成的元组。每种原色都可以采用 0 到 255 之间的整数,达到 1670 万种独特的颜色。但是,在迭代次数附近,您的调色板通常包含比这少得多的内容。
注意:调色板中的颜色数量不一定必须等于最大迭代次数。毕竟,在您运行递归公式之前,不知道会有多少稳定性值。当您启用平滑时,分数转义计数的数量可能大于迭代次数!
如果您想测试几个不同的调色板,那么引入帮助函数以避免一遍又一遍地重新输入相同的命令可能会很方便:
>>> from PIL import Image
>>> from mandelbrot import MandelbrotSet
>>> from viewport import Viewport
>>> def paint(mandelbrot_set, viewport, palette, smooth):
... for pixel in viewport:
... stability = mandelbrot_set.stability(complex(pixel), smooth)
... index = int(min(stability * len(palette), len(palette) - 1))
... pixel.color = palette[index % len(palette)]
该函数将MandelbrotSet实例作为参数,后跟Viewport、调色板和平滑标志。调色板必须是具有 Pillow 期望的红色、绿色和蓝色通道值的元组列表。请注意,一旦您计算了手头像素的浮点稳定性,您必须在将其用作调色板中的整数索引之前对其进行缩放和钳制。
Pillow 只理解颜色通道的 0 到 255 范围内的整数。但是,使用0 到 1 之间的归一化小数值通常可以防止您的大脑紧张。您可以定义另一个函数来反转规范化过程以使 Pillow 库满意:
>>> def denormalize(palette):
... return [
... tuple(int(channel * 255) for channel in color)
... for color in palette
... ]
此函数将分数颜色值缩放为整数值。例如,它将一个带有数字的元组转换(0.13, 0.08, 0.21)为另一个由以下通道强度组成的元组:(45, 20, 53).
巧合的是,Matplotlib 库包含几个具有此类标准化颜色通道的颜色图。一些颜色图是固定的颜色列表,而另一些则能够对作为参数给出的值进行插值。您现在可以将其中一个应用到您的 Mandelbrot 集可视化:
>>> import matplotlib.cm
>>> colormap = matplotlib.cm.get_cmap("twilight").colors
>>> palette = denormalize(colormap)
>>> len(colormap)
510
>>> colormap[0]
[0.8857501584075443, 0.8500092494306783, 0.8879736506427196]
>>> palette[0]
(225, 216, 226)
twilight颜色图是 510 种颜色的列表。调用denormalize()它后,您将获得适合您的绘画功能的调色板。在调用它之前,您需要定义更多变量:
>>> mandelbrot_set = MandelbrotSet(max_iterations=512, escape_radius=1000)
>>> image = Image.new(mode="RGB", size=(512, 512))
>>> viewport = Viewport(image, center=-0.7435 + 0.1314j, width=0.002)
>>> paint(mandelbrot_set, viewport, palette, smooth=True)
>>> image.show()
这将产生与以前相同的螺旋,但外观更具吸引力:
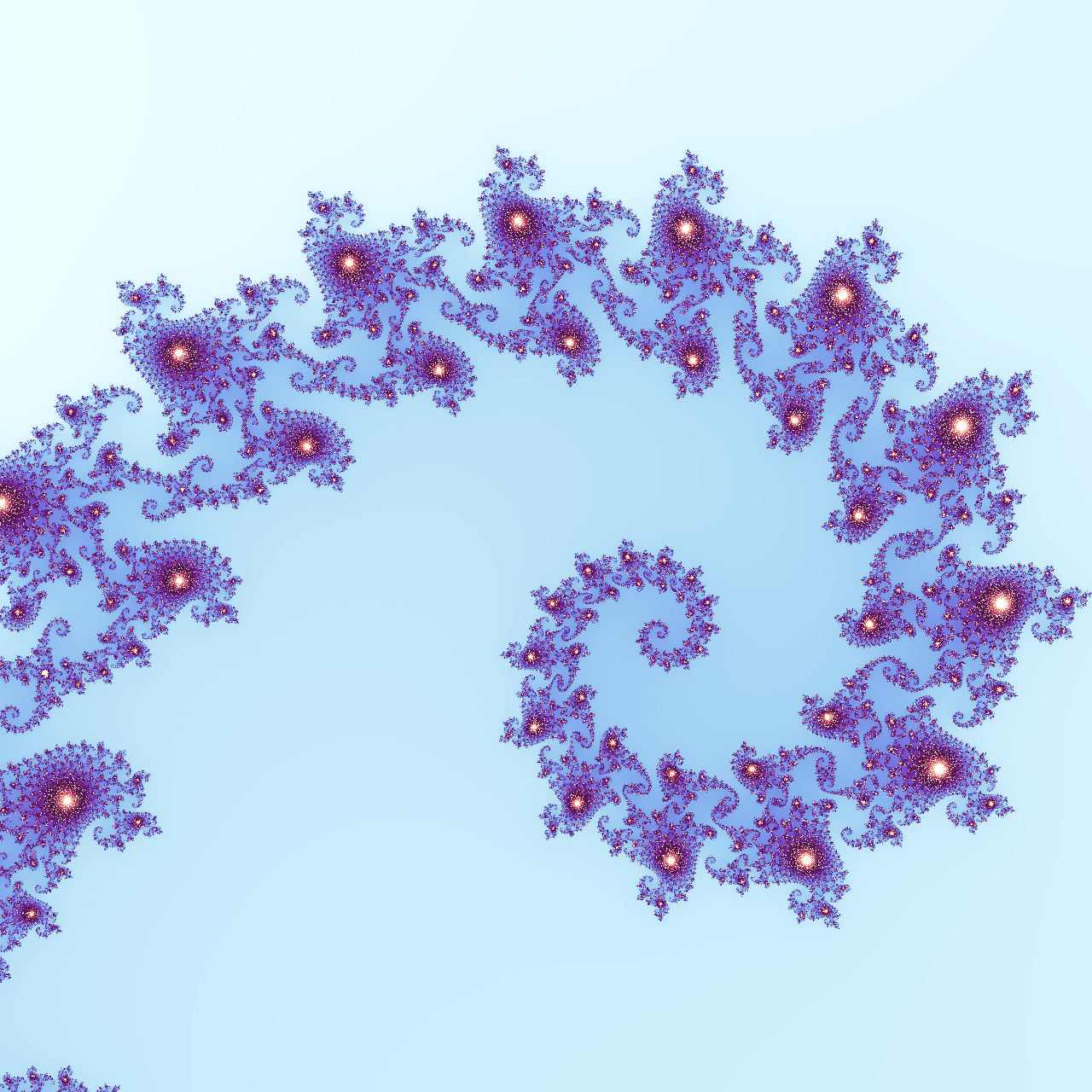
使用暮光调色板可视化的螺旋
随意尝试 Matplotlib 中包含的其他调色板或他们在文档中提到的第三方库之一。此外,Matplotlib 允许您通过将_r后缀附加到颜色图的名称来反转颜色顺序。您还可以从头开始创建调色板,如下所示。
假设您想强调分形的边缘。在这种情况下,您可以将分形分成三个部分并为每个部分分配不同的颜色:
>>> exterior = [(1, 1, 1)] * 50
>>> interior = [(1, 1, 1)] * 5
>>> gray_area = [(1 - i / 44,) * 3 for i in range(45)]
>>> palette = denormalize(exterior + gray_area + interior)
为您的调色板选择一个整数,例如 100 种颜色,将简化公式。然后,您可以拆分颜色,使 50% 到外部,5% 到内部,剩下的 45% 到中间的灰色区域。通过将 RGB 通道设置为完全饱和,您希望外部和内部都保持白色。但是,中间地带应该逐渐从白色变为黑色。
不要忘记将视口的中心点设置为 -0.75,并将其宽度设置为 3.5 个单位以覆盖整个分形。在此缩放级别,您还需要减少迭代次数:
>>> mandelbrot_set = MandelbrotSet(max_iterations=20, escape_radius=1000)
>>> viewport = Viewport(image, center=-0.75, width=3.5)
>>> paint(mandelbrot_set, viewport, palette, smooth=True)
>>> image.show()
当您再次调用paint()并显示图像时,您将看到 Mandelbrot 集的清晰边界:
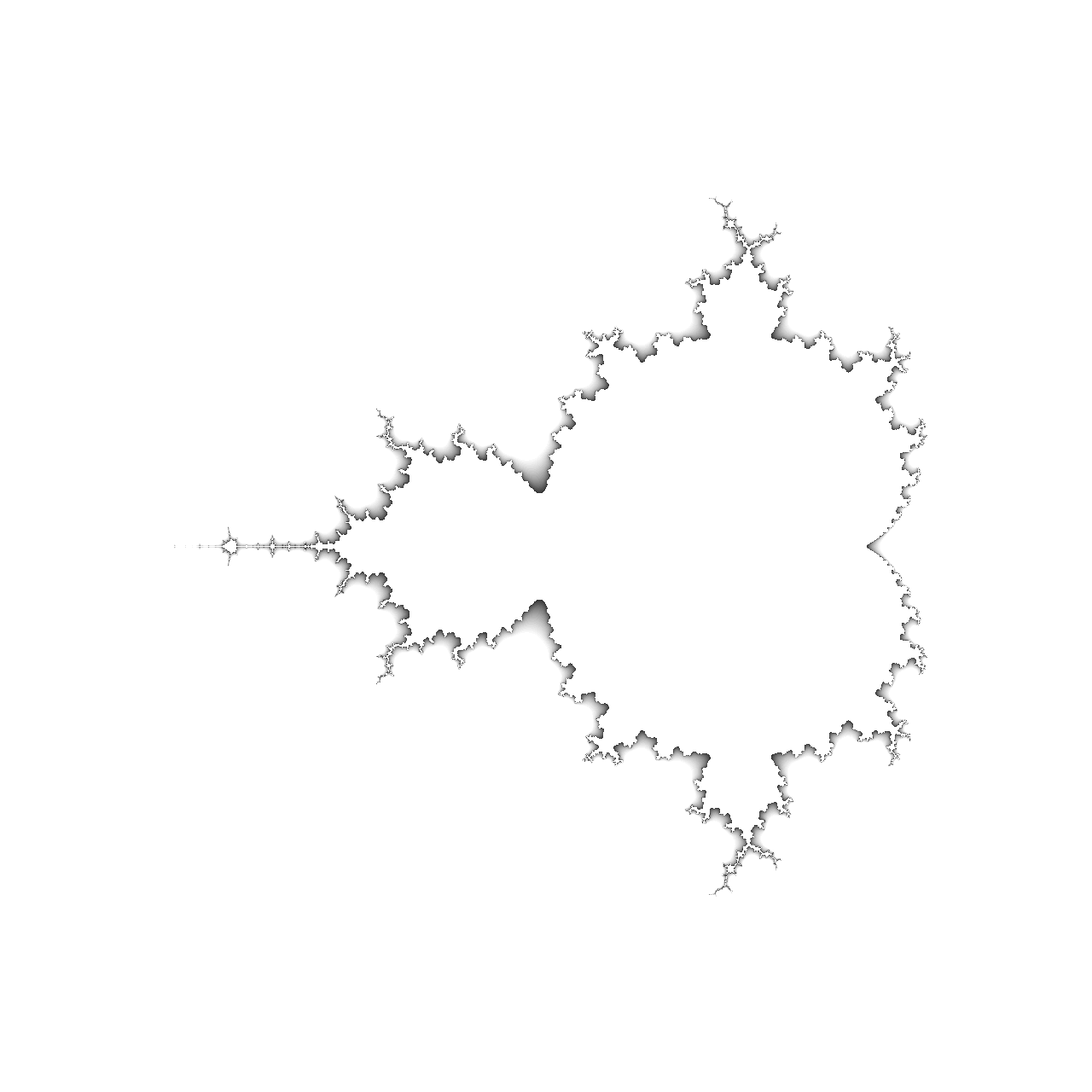
带出分形边缘的自定义调色板
从白色到黑色的连续过渡,然后突然跳到纯白色,会产生一种阴影浮雕效果,突出分形的边缘。您的调色板将一些固定颜色与称为颜色渐变的平滑颜色渐变相结合,您将在接下来进行探索。
颜色渐变
您可能会将渐变视为连续的调色板。最常见的颜色渐变类型是线性渐变,它使用线性插值来查找两种或多种颜色之间最接近的值。当您混合黑色和白色以投射阴影时,您刚刚看到了这种颜色渐变的示例。
现在,您可以计算出您打算使用的每个渐变的数学计算或构建一个通用渐变工厂。此外,如果您想以非线性方式分配颜色,那么SciPy是您的朋友。该库带有线性、二次和三次插值方法等。以下是您可以利用它的方法:
>>> import numpy as np
>>> from scipy.interpolate import interp1d
>>> def make_gradient(colors, interpolation="linear"):
... X = [i / (len(colors) - 1) for i in range(len(colors))]
... Y = [[color[i] for color in colors] for i in range(3)]
... channels = [interp1d(X, y, kind=interpolation) for y in Y]
... return lambda x: [np.clip(channel(x), 0, 1) for channel in channels]
您的新工厂函数接受定义为浮点值三元组的颜色列表和带有 SciPy 公开的插值算法名称的可选字符串。大写X变量包含基于颜色数量介于 0 和 1 之间的标准化值。大写Y变量为每种颜色保存三个序列的 R、G 和 B 值,并且该channels变量具有每个通道的插值函数。
当你调用make_gradient()一些颜色时,你会得到一个新函数,它可以让你插入中间值:
>>> black = (0, 0, 0)
>>> blue = (0, 0, 1)
>>> maroon = (0.5, 0, 0)
>>> navy = (0, 0, 0.5)
>>> red = (1, 0, 0)
>>> colors = [black, navy, blue, maroon, red, black]
>>> gradient = make_gradient(colors, interpolation="cubic")
>>> gradient(0.42)
[0.026749999999999954, 0.0, 0.9435000000000001]
请注意,渐变颜色(例如上例中的黑色)可以重复并以任何顺序出现。要将渐变连接到您的调色板感知绘画函数,您必须确定相应调色板中的颜色数量并将渐变函数转换为非规范化元组的固定大小列表:
>>> num_colors = 256
>>> palette = denormalize([
... gradient(i / num_colors) for i in range(num_colors)
... ])
...
>>> len(palette)
256
>>> palette[127]
(46, 0, 143)
您可能会想直接针对稳定性值使用梯度函数。不幸的是,这在计算上太昂贵了,把你的耐心推到了极限。您想预先计算所有已知颜色的插值,而不是每个像素。
最后,在构建渐变工厂、创建渐变函数和非规范化颜色之后,您可以使用渐变调色板绘制 Mandelbrot 集:
>>> mandelbrot_set = MandelbrotSet(max_iterations=20, escape_radius=1000)
>>> paint(mandelbrot_set, viewport, palette, smooth=True)
>>> image.show()
这将产生一个发光的霓虹灯效果:

不断增加迭代次数,直到您对图像中的平滑量和细节数量感到满意为止。但是,请查看接下来会发生什么以获得最佳结果和最直观的颜色处理方式。
颜色模型
到目前为止,您一直在研究红色、绿色和蓝色 (RGB) 分量的领域,这并不是思考颜色的最自然方式。幸运的是,有其他颜色模型可以让您表达相同的概念。一种是色相、饱和度、亮度(HSB)颜色模型,也称为色相、饱和度、值(HSV)。
注意:不要将 HSB 或 HSV 与另一种颜色模型混淆:色相、饱和度、亮度 (HSL)。
与 RGB 一样,HSB 模型也具有三个分量,但它们与红色、绿色和蓝色通道不同。您可以将 RGB 颜色想象为包含在 3D 立方体中的一个点。但是,同一点在 HSB 中具有柱坐标:
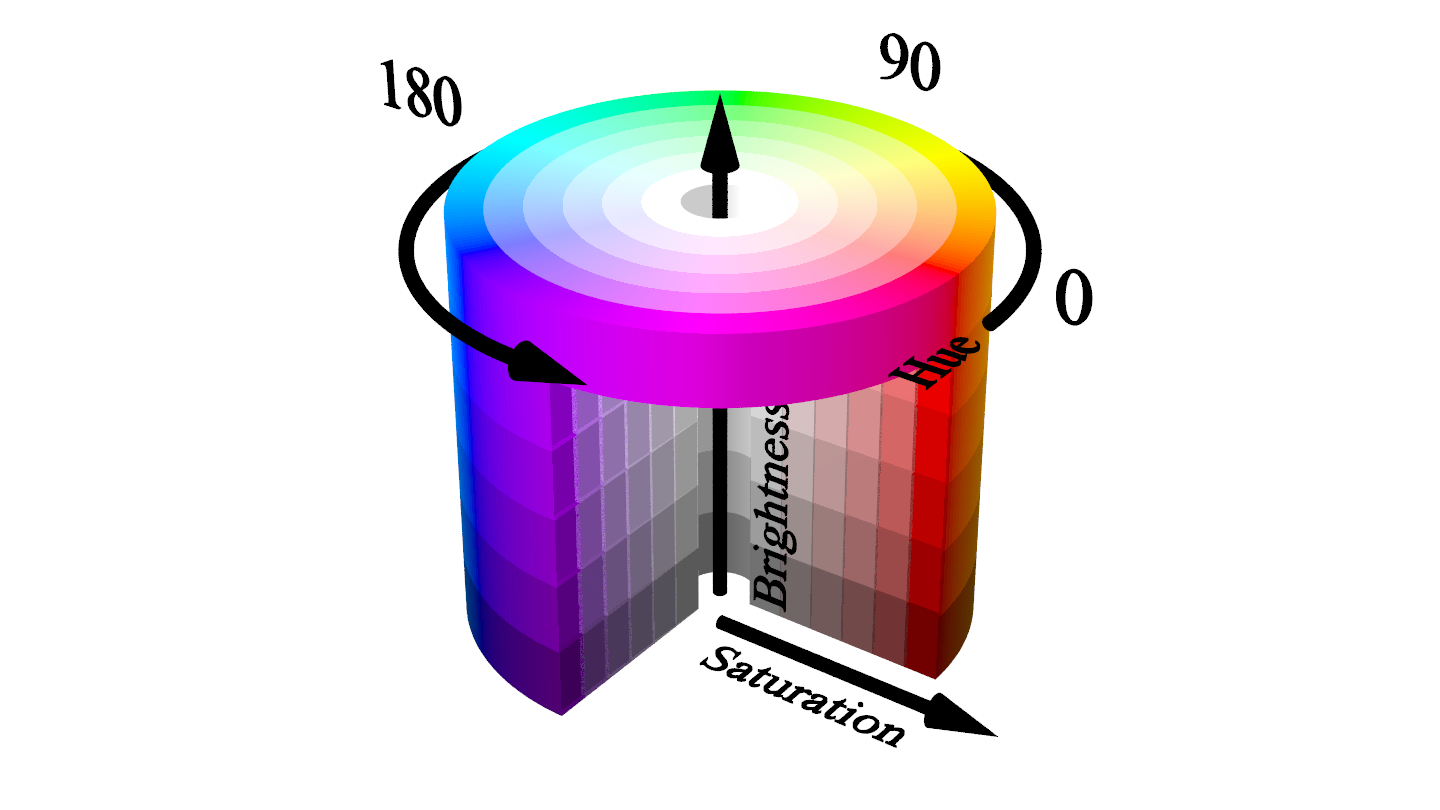
色相饱和度亮度缸
三个 HSB 坐标是:
- 色调:在 0° 和 360° 之间逆时针测量的角度
- 饱和度:圆柱体的半径在 0% 到 100% 之间
- 亮度:圆柱体的高度在 0% 到 100% 之间
要在 Pillow 中使用此类坐标,您必须将它们转换为熟悉的 0 到 255 范围内的 RGB 值元组:
>>> from PIL.ImageColor import getrgb
>>> def hsb(hue_degrees: int, saturation: float, brightness: float):
... return getrgb(
... f"hsv({hue_degrees % 360},"
... f"{saturation * 100}%,"
... f"{brightness * 100}%)"
... )
>>> hsb(360, 0.75, 1)
(255, 64, 64)
Pillow 已经提供了getrgb()您可以委托的辅助函数,但它需要一个带有编码 HSB 坐标的特殊格式的字符串。另一方面,您的包装函数接受hue度数和两者saturation,并brightness作为规范化的浮点值。这使您的函数与零到一之间的稳定性值兼容。
有几种方法可以将稳定性与 HSB 颜色联系起来。例如,您可以通过将稳定性缩放到 360° 度来使用整个色谱,使用稳定性来调制饱和度,并将亮度设置为 100%,如下面的 1 所示:
>>> mandelbrot_set = MandelbrotSet(max_iterations=20, escape_radius=1000)
>>> for pixel in Viewport(image, center=-0.75, width=3.5):
... stability = mandelbrot_set.stability(complex(pixel), smooth=True)
... pixel.color = (0, 0, 0) if stability == 1 else hsb(
... hue_degrees=int(stability * 360),
... saturation=stability,
... brightness=1,
... )
...
>>> image.show()
要将内部涂成黑色,请检查像素的稳定性是否恰好为 1,并将所有三个颜色通道设置为零。对于小于 1 的稳定性值,外部的饱和度会随着与分形的距离而减弱,并且色调会遵循 HSB 圆柱体的角度维度:
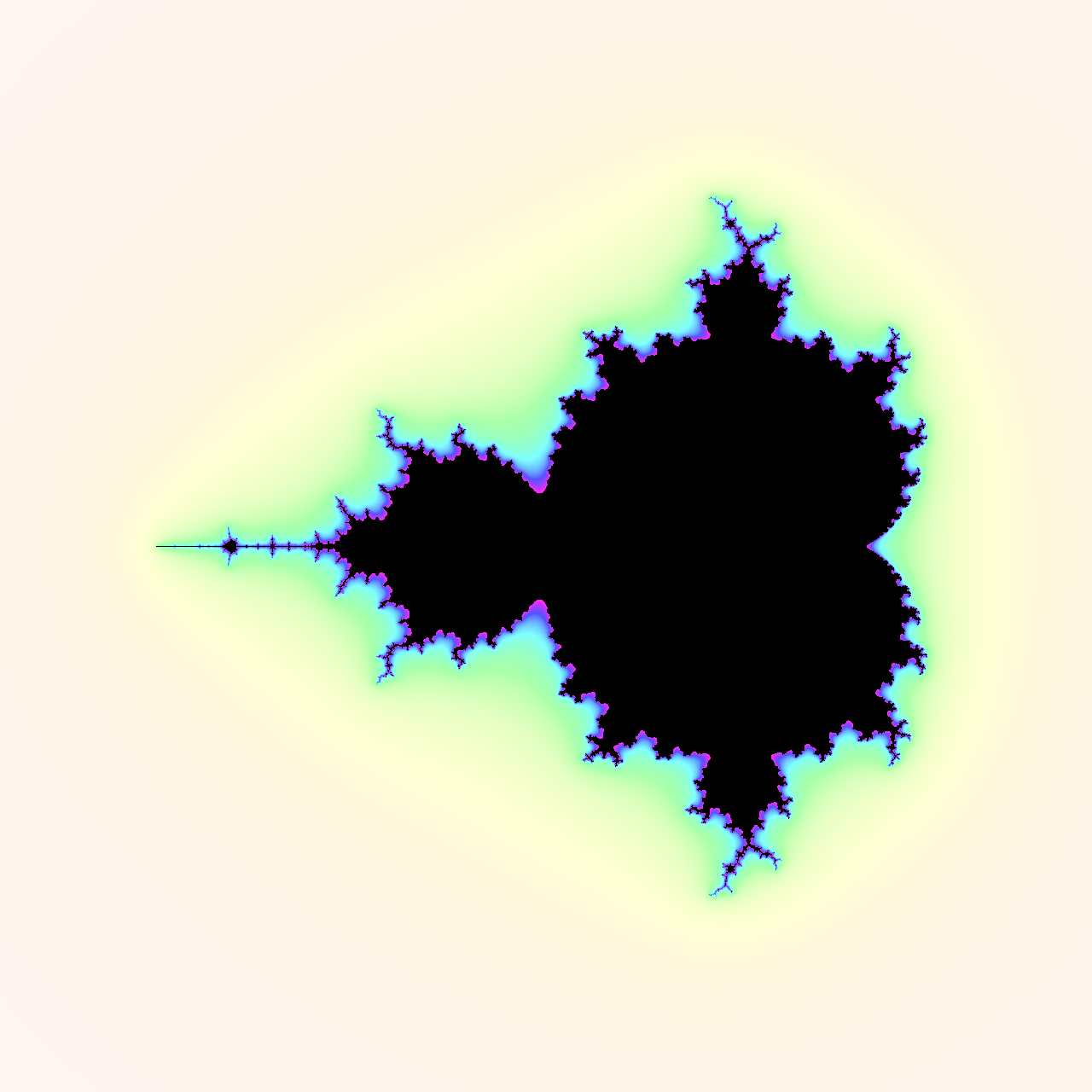
使用 HSB 颜色模型可视化的 Mandelbrot 集
当您靠近分形时,角度会增加,颜色会从黄色变为绿色、青色、蓝色和洋红色。您看不到红色,因为分形的内部总是涂成黑色,而外部最远的部分几乎没有饱和度。请注意,将圆柱体旋转 120° 可让您在其底部定位三种原色(红色、绿色和蓝色)中的每一种。
不要犹豫,尝试以不同的方式计算 HSB 坐标,看看会发生什么!
结论
现在您知道如何使用 Python 来绘制和绘制 Benoît Mandelbrot 发现的著名分形了。你已经学会了用颜色、灰度和黑白来可视化它的各种方法。您还看到了一个实际示例,说明了复数如何帮助在 Python 中优雅地表达数学公式。
在本教程中,您学习了如何:
- 将复数应用于实际问题
- 查找Mandelbrot和Julia集的成员
- 使用Matplotlib和Pillow将这些集合绘制为分形
- 对分形进行丰富多彩的艺术表现
您可以通过单击下面的链接下载本教程中使用的完整源代码:
- 点赞
- 收藏
- 关注作者


评论(0)