@[TOC](R 聚类分析)

1 常规聚类过程

• 1、首先用dist()函数计算变量间距离 dist.r = dist(data, method=” “)
• 其中method包括：”euclidean”, “maximum”, “manhattan”,
• “canberra”, “binary” or “minkowski”。

• 2、再用hclust()进行聚类 hc.r = hclust(dist.r, method = “ ”)
• 其中聚类的方法method包括7：”ward”, “single”, “complete”,
• ”average”, “mcquitty”, “median” or “centroid”。

• 3、画图 plot(hc.r, hang = -1,labels=NULL) 或者plot(hc.r, hang =
0.1,labels=F)

• hang 等于数值，表示标签与末端树杈之间的距离，若是负数，则
表示末端树杈长度是0，即标签对齐。
• labels 表示标签，默认是NULL，表示变量原有名称。

如果参与聚类的变量的量纲不同会导致错误的聚类结果。因此在聚类过程进行之前必须
对变量值进行标准化，即消除量纲的影响。如果参与聚类的变量纲相同，可以使用系统
默认值None，要对数据不要进行标准化处理。

2 变量的相似度计算方法

1 连续型属性的相似度计算方法

2 二值离散型属性的相似度计算方法

数据样本的二值离散型属性的取值情况

对称的二值离散型属性

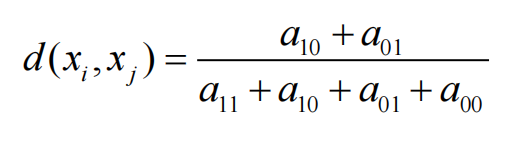
不对称的二值离散型属性

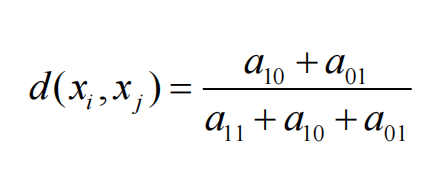
3 多值离散型属性的相似度计算方法

多值离散型属性的相似度

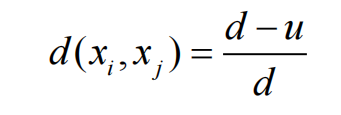
d为数据集中的属性个数，u为样本xi和xj取值
相同的属性个数

4 混合类型属性的相似度计算方法

• 对于包含混合类型属性的数据集的相似度通常有两种计算方法：
• 将属性按照类型分组，每个新的数据集中只包含一种类型的属性；之后对每个数据集进
行单独的聚类分析
• 把混合类型的属性放在一起处理，进行一次聚类分析

• r语言中使用
• dist(x, method = “euclidean”,diag = F, upper = FALSE, p = 2)
• 来计算距离。其中x是样本矩阵或者数据框。method表示计算哪种距离。method的取值有：
euclidean 欧几里德距离，就是平方再开方。
maximum 切比雪夫距离
manhattan 绝对值距离
canberra Lance 距离
minkowski 明科夫斯基距离，使用时要指定p值
binary 定性变量距离. • r语言中使用scale(x, center = TRUE, scale = TRUE) 对数据矩阵
做中心化和标准化变换。如只中心化 scale(x,scale=F) 。

• 对变量进行分类时，不计算距离，而是计算变量间的相关系数。
y <- scale(x, center = F, scale = T)/sqrt(nrow(x)-1)
• C <- t(y) %*% y • 相关系数用cor函数

数据收集和整理系统；雏菊
• Dissimilarity Matrix Calculation
• daisy {cluster}
• Description
• 计算数据库中成对数据之间的距离（差异dissimilarities
(distances)）。原始变量可能是混合模型或设置 metric =
“gower” ，这时会使用Gower’s formula广义公式. • Usage
• daisy(x, metric = c(“euclidean”, “manhattan”, “gower”),
stand = FALSE, type = list(), weights = rep.int(1, p),
warnBin = warnType, warnAsym = warnType, warnConst =
warnType, warnType = TRUE)

3、 k平均（k-means）聚类算法

• 发明于1956年， 最常见，采用Lloyd algorithm迭代探索法。
• 劳埃德算法首先把输入点分成k个初始化分组，可以是随机的或者使用一些启发式数据。
• 然后计算每组的均值，根据均值把对象分到离它最近的中心，重新确定分组。
• 继续重复不断地计算中心并重新分组，直到收敛，即对象不再改变分组（“中心”位置不再改变）。
• 划分聚类方法对数据集进行聚类时包含三个要点：
• 选定某种距离作为数据样本间的相似性度量
• 选择评价聚类性能的准则函数
• 选择某个初始分类，之后用迭代的方法得到聚类结果，使得评价聚类的准则函数取得最优值 .

r语言中Kmeans聚类方法
kmeans(x, centers, iter.max = 10, nstart = 1, algorithm =
c(“Hartigan-Wong”, “Lloyd”, “Forgy”, “MacQueen”),
trace=FALSE)
• ## S3 method for class ‘kmeans’
fitted(object, method = c(“centers”, “classes”), …)
• centers是初始类的个数或者初始类的中心。iter.max是
最大迭代次数。当centers是数字时，nstart是随机集合
的个数。algorithm是算法，默认是第一个。

参数

x 数值型矩阵，或者一个对象，可以被转换成矩阵形式 (例如数值型向量、
所有列都是数值的数据框).
centers 聚类的个数 k, 或一组初始簇的中心.如果是一个数，将从x中随机选择几行
作为初始的中心.
iter.max 最大迭代次数
nstart 如果 centers 是一个数，该参数给出应该随机选择几个子集
algorithm 字符串。该参数可以被简写， "Lloyd" and"Forgy" 是可选项
object R中"kmeans"的一个对象，主要是 ob <- kmeans(..)的ob结果
method 字符串，可以被简写.该参数如果是 "centers" ，则拟合返回簇的中心(每一
个输入值有一个结果) ，如果该参数是"classes"，则拟合结果返回分配到的
簇的一个向量.
trace 逻辑值或整数，可用的方法就是默认项("Hartigan-Wong"):如果该参数是整
数，或者T，生成算法处理过程的信息。数值越大生成的信息越大

输出

cluster 一个整数(from 1:k)向量，表明每个点在哪个簇cluster中.
centers 簇中心构成的矩阵.
totss The total sum of squares，总平方和.
withinss
Vector of within-cluster sum of squares, 向量，簇内平方和，每个簇内一
个内容.
tot.withinss Total within-cluster sum of squares, i.e. sum(withinss).簇内总平方和
betweenss The between-cluster sum of squares, i.e. totss-tot.withinss.簇间的平方和
size The number of points in each cluster.每一个簇内的点数
iter The number of (outer) iterations.迭代次数
ifault 整数，表明可能的算法问题，针对专家

Examples
• # 前边例子
• #a 2-dimensional example
• x <- rbind(matrix(rnorm(100, sd = 0.3), ncol = 2),matrix(rnorm(100, mean = 1, sd = 0.3), ncol = 2) )
• colnames(x) <- c(“x1”, “x2”)
• ###聚类
• (cl <- kmeans(x, 2))

K-means clustering with 2
clusters of sizes 48, 52
Cluster means:
Clustering vector:
Within cluster sum of
squares by cluster:
Available components:

聚类结果详细结论

画聚类图


K均值聚类方法缺点

K均值聚类方法是基于均值的，所以它对异常
值是敏感的。
K均值聚类一般使用欧几里得距离

k中心点聚类pam()和pamk() {fpc}

• k中心点聚类和k均值聚类算法很接近，主要的区别是：在k均值算法中，它的中心代表一个类，而在k中心点算法中将与类中心对象最接近的点作为一个类
• PAM（Partitioning Around Medoids）的思想是基于距离聚类，具有良好的抗噪声、抗偏离点的能力。
• 它的弱点是不能处理大量的数据，但是经过改良的算法CLARA算法选取数据的多个样本
• PAM和CLARA这两个算法在R中可以通过包‘cluster’中的函数pam()和clara()实现，这两个函数都需要指定聚类的数量k。但是在包‘fpc’中的函数pamk()可以通过调用pam()或者
clara()选择效果最优的聚类数。

• library(fpc) • pamk.result <- pamk(iris2)
• pamk.result： ##查看结果
• $pamobject
• Medoids: • Clustering vector:
• Objective function:
• Available components:
• nc
• crit

summary(pamk.result)
pamk.result$pamobject
pamk.result$nc
table(pamk.result$pamobject$clustering, iris$Species)
setosa versicolor virginica
1 50 1 0 
2 0 49 50

• ##分为三类
• pam.result <- pam(iris2, 3)
• ##检验聚类结果
• table(pam.result$clustering, 
iris$Species)
39
setosa versicolor virginica
1 50 0 0
2 0 48 14 
3 0 2 36

轮廓系数

• 轮廓系数（Silhouette coefficient）适用于实际类别信息未知的情况。对于单个样本，设a 是与它同类别中其他样本的平均距离，b 是与它距离最近不同类别中样本的平均距离，轮廓系数为：
• s=(b−a)/max(a,b) 。 • 对于一个样本集合，它的轮廓系数是所有样本轮廓系数的平均值。
• 轮廓系数取值范围是[−1,1] ，同类别样本越距离相近且不同类别样本距离越远，分数越高

4 层次聚类方法

 层次聚类方法对给定的数据集进行层次的分解，直到某种条件满足为止。具体可分为：
凝聚的层次聚类：一种自底向上的策略，首先将每个对象作为一个类，然后合并这些原子类为越来越大的类，直到某个终结条件被满足。
分裂的层次聚类：采用自顶向下的策略，它首先将所有对象置于一个类中，然后逐渐细分为越来越小的类，直到达到了某个终结条件。
 无论哪种方法，聚类原则都是相近的聚为一类，即距离最近或最相似的聚为一类。以上两种方法是方向相反的两种聚类过程
 层次凝聚的代表是AGNES算法，层次分裂的代表是DIANA算法。

r语言中进行层次聚类

• hclust(d, method = “complete”, members=NULL) 来进行层次聚类。其中d为距离矩阵；
• method表示类的合并方法，有：
single 最短距离法
complete 最长距离法
median 中间距离法
mcquitty 相似法
average 类平均法
centroid 重心法
ward 离差平方和法
• stats包中的hclust（）函数进行聚类。系统聚类一般首先使用dist（）函数计算欧式距离，再使用hclust（）函数展开系统聚类。

层次聚类例

x<-c(1,2,3,7,8,9,15)###x为1行7列 • dim(x)=c(7,1) ###x为7行1列 • d=dist(x) ##distance,差的绝对值
• ### 生成系统聚类函数hclust： • hc1<-hclust(d,"single")
• hc2<-hclust(d,"complete")
• hc3<-hclust(d,"median")
• hc4<-hclust(d,"average")
• ###其中hclust表示系统聚类计算函
数，single、complete、median、
average
• ##分别表示最短距离法、最长距离
法、中间距离法、类平均法。
• ##聚类结果可视化，画图
• win.graph(width=5,height=4)
• par(mfrow=c(2,2))
• plot(hc1)
• plot(hc2)
• plot(hc3)
• plot(hc4)

对鸢尾花数据集进行层次聚类

• ##从鸢尾花数据集中抽取40个样本，避免聚
类图上的点拥挤甚至重叠在一起
• idx <- sample(1:dim(iris)[1], 40)
• irisSample <- iris[idx,]
• irisSample $Species <- NULL • hc <- hclust(dist(irisSample), method="ave") • plot(hc, hang = -1, labels=iris$Species[idx])

基于密度的聚类

算法： DBSCAN
通过检查数据集中每个对象的ε-邻域来寻找聚类。如果一个点p的ε-邻域包含多于MinPts个对象，则创建一个p作为核心对象的新类。然后反复地寻找从这些核心对象直接密
度可达的对象。当没有新的点可以被添加到任何类时，该过程结束。
只要一个区域中的点的密度大于某个阈值，就把它加到与
之相近的聚类中去。

r使用包‘fpc’实现DBSCAN算法

• dbscan(data, eps, MinPts, scale, method, seeds, show
plot, countmode) • eps是可达距离，定义邻域的大小，距离的半径，
• minpts是最少多少个点，邻域eps内所有满足为一
类点的数量最小值要求。
• scale是否标准化,method 有三个值raw,dist,hybird 。
showplot画不画图，0不画，1和2都画。
• Countmode，用来显示计算进度。

鸢尾花数据集基于密度的聚类算法

• library(fpc) • newiris <- iris[1:4]##或iris3 <- iris[-5] # 移除分
类标签
• ds <- dbscan(newiris, eps=0.42, MinPts=5)
• ds
• plot(ds, newiris) ##结果为4*4的矩阵图

5 聚类之EM算法

定义：在统计计算中，最大期望（EM）算法是在概率模型中（E步）寻找参数最大似然估计或者最大后验估计（M步）的算法，其中概率模型依赖于无法观测的隐藏变量
（LatentVariable），聚类应用中就是隐藏的类别。 • 期望最大算法是一种从不完全数据或有数据丢失的数据集（存在隐含变量）中求解概率模型参数的最大似然估计方
法。
• 该算法既简单又复杂，简单的是其仅包含了两个步骤（E步和M步）就能完成强大的功能，复杂的是数学推理涉及到比较繁杂的概率公式。下面先举一个简单的例子也许就
能大致明白这里的E步和M步了。

• 为了理解EM算法，做一次EM算法的步骤：
• 1）假定初始的P(A)和P(B)值，不妨P(A)=0.6，P(B)=0.5。 • 2）对于第一次试验，A硬币或B硬币出现5次正面朝上的
概率，该步为E步

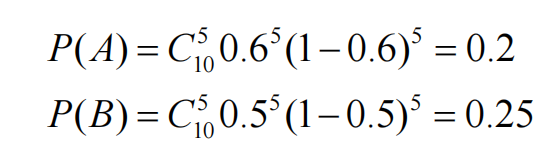
从而断定，第一次可能投掷B硬币的概率比较大，依次可以计算后四次用某种硬币投掷的可能性.

R语言中提供了EM算法的软件包

• Mclust(){mclust}可以实现EM聚类，
• Mclust(data, G = NULL, modelNames = NULL, prior = NULL, control = emControl(), initialization = NULL, warn = mclust.options("warn"), 
...)
• data提供用于分析的数据集，切记数据集中不可有分类变量；
• G指定聚类的数目，默认为1:9类；
• modelNames指定EM聚类过程中的拟合模型；
• prior指定先验值，默认不指定；
• control指定EM算法的控制参数，如收敛阈值、最大迭代次数等
• initialization为算法指定初始值；

• temp<-cmdscale(dist.r,k=2) 
• x<-temp[,1]
• y<-temp[,2]
• library(ggplot2)
• p<-ggplot(data.frame(x,y),aes(x,y))
• p+geom_point(size=3,alpha=0.8,
• aes(colour=factor(result)))

6 R 实践

K-means聚类

创建随机数进行聚类

c1<-cbind(rnorm(40,2,1),rnorm(40,2,3))
c2<-cbind(rnorm(30,3,1),rnorm(30,10,9))
c3<-cbind(rnorm(30,15,1),rnorm(30,20,9))
v1=rbind(c1,c2,c3)
plot(v1)
cl=kmeans(v1,3)
cl$betweenss  #Sum of squares between clusters
cl$iter       #Number of iterations
plot(v1,col=cl$cluster)
points(cl$centers,pch="+",col=cl$cluster)

有量纲影响的数据进行标准化后表现更好，这里没有第一次创建的随机数太好了，没表现出来

#When the data units are inconsistent,you can standardize the data and make the clustering standard

v2=scale(v1)
v2
cl1=kmeans(v2,3)
plot(v2,col=cl1$cluster)
points(cl1$centers,pch="*",col="blue")

以iris为例子

data(iris)
fix(iris)
newdata=iris[,-ncol(iris)]

newdata
cl=kmeans(newdata,3)
cl$cluster
cbind(iris$Species,cl$cluster)

循环寻找最适合的类别数，并画图观察

USArrests
clu=kmeans(USArrests,3)
clu$cluster
USArrests[clu$cluster==2,]

kk=1:8
pp=NULL
for (i in kk) {
  clf=kmeans(USArrests,i)
  pp[i]=clf$betweenss/clf$totss
}
pp
plot(kk,pp,type="l",ylab = "比例",main="折线图")
cll=kmeans(scale(USArrests),4)
cll

层次聚类

?hclust
dd=iris[,-ncol(iris)]
hc1=hclust(dist(dd),method = "single")
plot(hc1)
plot(hc1,hang=2)
cutree(hc1,k=2) #K is classification quantity