【数据结构系列】双向链表
课后习题
上一篇文章中我们说到单链表,然后最后有一道习题,不知道大家有没有做出来,为了照顾一些还不太会的同学,这里专门对这道题进行一个简单的讲解,先来看看原题内容:
有一个带头结点的单链表L = {a1,b1,a2,b2,…,a(n),b(n)},试设计一个算法将其拆分成两个带头结点的单链表L1和L2,L1 = {a1,a2,…,a(n)},L2 = {b(n),b(n - 1),…,b(1)},要求L1使用L的头结点。
从题目中我们就可以看出,L1通过尾插法建立,L2通过头插法建立。
这道题本身并没有太大难度,我们通过画图的方式来分析一下,如下图是单链表L的一部分:

既然是要拆分成两个链表,我们需要定义出两个结点类型的变量p,q,可以先让p指向第一个有效结点,即:存放数据a1的结点,然后将a1插入到L1中;接着让q指向p的下一个结点,即:存放数据b1的结点,然后将b1插入到L2中,以此循环,即可完成。
看代码如何实现:
PNode split(PNode L){
PNode L1,L2,R1,p,q;
L1 = L;//这里我们仍然使用链表L的头结点作为链表L1的头结点
R1 = L1;//R1为链表L1的尾结点,初始指向头结点
p = L->next;//p初始指向链表L的第一个有效结点,用于找出链表L1的结点
//创建链表L2的头结点
L2 = (PNode) malloc(sizeof(Node));
if(L2 == NULL){
printf("内存分配失败,程序终止!\n");
exit(-1);
}
L2->next = NULL;//L2的头结点初始指针域为NULL
while(p != NULL){
q = p->next;//q初始指向链表L的第二个有效结点,用于找出链表L2的结点
//尾插法插入结点到链表L1
R1->next = p;
R1 = p;
//判断q是否空
if(q == NULL){
break;
}
//将p后移
p = q->next;
//头插法插入结点到链表L2
q->next = L2->next;
L2->next = q;
}
//L1尾结点指针域为NULL
R1->next = NULL;
return L2;//返回链表L2的头结点
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
如果你掌握了头插法和尾插法的话,这道题相信难不倒你,唯一需要注意的就是循环里有一个判断条件,为什么要判断q非空?而且该判断语句的位置可不能乱写,否则程序就会出错。这里其实涉及到两种情况,链表L的结点数为奇数个或者结点数为偶数个,我们先看奇数个(假设链表L1有三个有效结点):

那么一开始,p将指向存储数据1的结点,而循环体的第一条语句就是找到了q,q为存储数据2的结点,当把p插入到链表L1之后,我们需要找出链表L1的下一个结点,也就是q->next,即:存放数据3的结点;之后把q结点插入到了链表L2,我们又需要找出链表L2的下一个结点,也就是p->next,而此时p为链表L的尾结点,它的指针域为NULL,所以此时q为NULL,而如果你没有对q进行非空判断的话,执行p=q->next语句时就会报错,程序就出现问题了,所以要在使用q变量之前对q进行一个非空的判断。
而如果是偶数个,就比如上面的这个链表,再加入一个结点,那么p就不会是链表的尾结点,而当执行p=q->next语句后,尾结点q的指针域为NULL,所以p为NULL,此时循环就终止了,也就不会出现程序错误。
编写测试代码:
void main(){
PNode pHead,L2;
int a[] = {1,2,3,4,5,6,7,8};
pHead = create_listT(a,8);
traverse_list(pHead);
L2 = split(pHead);
printf("链表L1:\t");
traverse_list(pHead);
printf("\n链表L2:\t");
traverse_list(L2);
getchar();
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
首先你肯定得建立一个链表作为链表L,如何建立链表在这里就不重复说了,不了解的可以看上一篇文章,然后将头结点传入,就拆分成了两个链表。
运行结果:
1 2 3 4 5 6 7 8 9
链表L1: 1 3 5 7
链表L2: 8 6 4 2
- 1
- 2
- 3
双链表定义
在文章开头我们对单链表进行了一个简单的复习,下面我们进入本篇文章的主题,双链表。
先来看看定义:
双向链表也叫双链表,是链表的一种,它的每个数据结点中都有两个,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。
从定义中能够知道,双链表和单链表的唯一区别就是,双链表多了一个能够指向直接前驱结点的指针域,能够实现双向访问。
那么在双链表中,我们假设每个结点的类型用Node表示,它应该有一个存储元素的数据域,这里用data表示,有一个存储直接后继结点地址的指针域,这里用next表示,还应该有一个存储直接前驱结点地址的指针域,这里用prior表示,Node类型定义如下:
typedef struct Node{
int data;
struct Node *next;
struct Node *prior;
}Node,*PNode;
- 1
- 2
- 3
- 4
- 5

双链表的初始化
那么如何建立一个空的双链表呢?
PNode create_list(){
//创建头结点
PNode pHead = (PNode) malloc(sizeof(Node));
pHead->next = NULL;
pHead->prior = NULL;
return pHead;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
非常简单,分配一块内存用于头结点,然后将头结点的两个指针域都置为NULL即可。
对于非空双链表的建立,我们同样需要掌握头插法和尾插法两种建立方式。
先看头插法:

这是一个双链表的头结点,如何通过头插法将一个结点插入到该链表上呢?
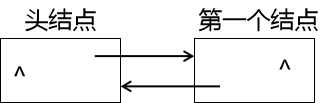
这样便完成了插入,如何实现呢?假设头结点为p,第一个结点为s,则s = p->next,此时s的指针域为NULL,然后s->prior = p,此时s结点指向它的直接前驱结点p(头结点),最后p->next = s,此时头结点指向第一个结点s。
貌似没有什么问题,然而再插入一个元素你就会发现,第一个结点的prior指针域没有改变,它仍然指向的是头结点,而事实上它应该指向第二个结点。
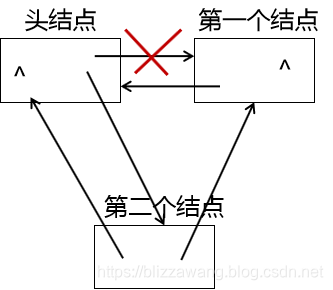
那该如何解决呢?我们可以发现一个规律,就是如果向一个空链表插入结点,也就是p->next = NULL的时候,是没有出现问题的,然而插入第二个结点的时候出现问题,所以我们可以对p的指针域做一个非空的判断,下面看代码实现:
PNode create_listH(int *a,int n){
PNode pHead,pNew;
int i;
//创建头结点
pHead = (PNode) malloc(sizeof(Node));
if(pHead == NULL){
printf("内存分配失败,程序终止!\n");
exit(-1);
}
pHead->next = NULL;//头结点初始指针域为NULL
for(i = 0;i < n;i++){
//创建新结点
pNew = (PNode) malloc(sizeof(Node));
if(pNew == NULL){
printf("内存分配失败,程序终止!\n");
exit(-1);
}
//保存数据
pNew->data = a[i];
pNew->next = pHead->next;//将新结点指针域置为NULL,该结点为链表的尾结点
//判断头结点后面是否有结点
if(pHead ->next != NULL){
//将头结点指向的结点的prior指针域指向新创建的结点
pHead->next->prior = pNew;
}
pHead->next = pNew;//头结点指向新结点
}
return pHead;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
为了验证代码的正确性,我们编写一个遍历函数,双链表的遍历方式和单链表一样,这里就直接贴代码了:
PNode create_list(){
//创建头结点
PNode pHead = (PNode) malloc(sizeof(Node));
pHead->next = NULL;
pHead->prior = NULL;
return pHead;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
编写测试代码:
void main(){
PNode pHead;
int a[] = {1,2,3,4,5,6};
pHead = create_listH(a,6);
traverse_list(pHead);
getchar();
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
运行结果:
6 5 4 3 2 1
- 1
- 2
下面看看尾插法如何建立双链表。

同样是这样的一个头节点,如何将第一个结点插入到链表上呢?
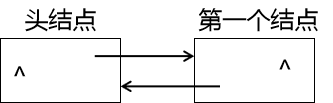
我们暂且把头节点叫做p,第一个结点叫做s,和单链表一样,我们仍然需要定义一个结点类型的pTail作为指向链表的尾结点,初始指向头结点pTail = p,然后我们只需pTail->next = s,也就是让头结点指向第一个结点,接着s->prior = pTail,让第一个结点指回头结点,最后pTail = s,此时插入的结点为链表的尾结点,不要忘了在结尾将pTail的next指针域置为空。
下面看代码实现:
PNode create_listR(int *a,int n){
PNode pHead,pNew,pTail;
int i;
//创建头结点
pHead = (PNode) malloc(sizeof(Node));
if(pHead == NULL){
printf("内存分配失败,程序终止!\n");
exit(-1);
}
pTail = pHead;//初始指向头结点
for(i = 0;i < n;i++){
//创建新结点
pNew = (PNode) malloc(sizeof(Node));
if(pNew == NULL){
printf("内存分配失败,程序终止!\n");
exit(-1);
}
//保存数据
pNew->data = a[i];
pTail->next = pNew;
pNew->prior = pTail;
pTail = pNew;
}
pTail->next = NULL;//尾结点指针域为NULL
return pHead;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
我们测试一下:
void main(){
PNode pHead;
int a[] = {1,2,3,4,5,6};
pHead = create_listR(a,6);
traverse_list(pHead);
getchar();
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
运行结果:
1 2 3 4 5 6
- 1
- 2
求双链表长度
这个和单链表的操作一样,没什么说的,直接看代码:
int length_list(PNode pHead){
int i = 0;
PNode p = pHead->next;
while(p != NULL){
i++;
p = p->next;
}
return i;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
这个在单链表中已经说过了,我就不测试了。
判断是否为空表
判断是否为空表也和单链表操作相同,看代码:
int isEmpty_list(PNode pHead){
if(pHead->next == NULL){
return 1;
}else{
return 0;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
插入结点
接下来又到了比较难的环节了,在双链表中的插入、删除操作和单链表十分类似,但又有些许不同,在双链表中,插入和删除的操作涉及到两个指针域的变化,所以相对要更复杂一些,但仔细品味,也很容易理解。
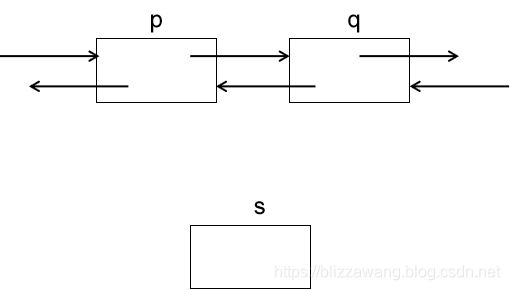
假设现在我需要将结点s插入到q的位置,则插入完成后链表结构如下:

那么如何实现插入呢?同样地,我们需要找到插入位置的前一个结点,例如在这里,需要将结点s插入到节点q的位置,则需要找到q的前一个结点也就是结点p,然后将结点s的指针域next指向p结点的指针域next,也就是让结点s指向结点q。
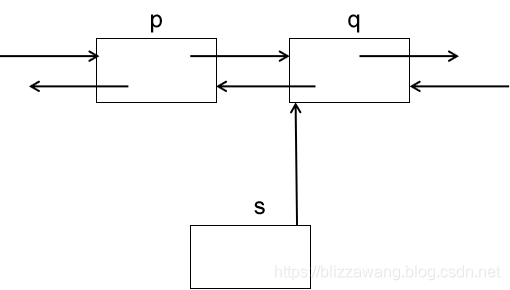
接着让结点q的指针域prior指向结点s,从而建立起结点s和结点q的双向关系。
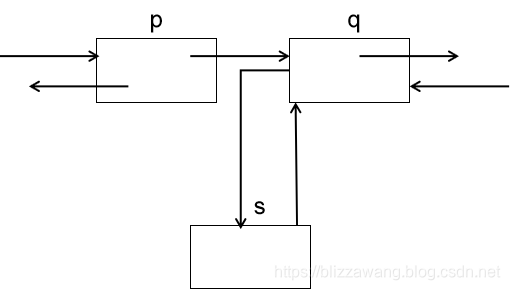
然后让结点s的指针域prior指向结点p,最后让结点p的指针域next指向结点s,建立起结点p和结点s的双向关系。
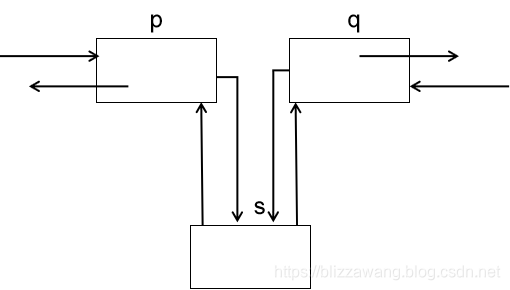
这样即可完成插入。
下面看代码实现:
int insert_list(PNode pHead,int pos,int val){
PNode p,pNew;
int len,i = 0;
p = pHead;//p初始指向头结点
len = length_list(pHead);
//判断pos值的合法性
if(pos < 1 || pos > len + 1){
return 0;
}
//找到插入位置的前一个结点
while(i < pos - 1 && p != NULL){
i++;
p = p->next;
}
if(p == NULL){
return 0;
}
//此时p为插入位置的前一个结点
//创建新结点
pNew = (PNode) malloc(sizeof(Node));
if(pNew == NULL){
printf("内存分配失败,程序终止!\n");
exit(-1);
}
//保存数据
pNew->data = val;
//插入结点
pNew->next = p->next;
//判断p是否为尾结点
if(p->next != NULL){
p->next->prior = pNew;
}
pNew->prior = p;
p->next = pNew;
return 1;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
插入操作中同样需要注意一个问题,那就是插入的位置如果是链表的末尾的话,通过循环找到的结点p即为链表的尾结点,而尾结点的指针域next为NULL,就无需考虑后面结点的指针域prior的指向问题,如果不加以判断,当你插入结点到链表末尾时,程序就会报错。
编写测试代码:
void main(){
PNode pHead;
int a[] = {1,2,3,4,5,6};
pHead = create_listR(a,6);
traverse_list(pHead);
if(insert_list(pHead,5,50)){
printf("插入后:\n");
traverse_list(pHead);
}else{
printf("插入失败!\n");
}
getchar();
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
运行结果:
1 2 3 4 5 6
插入后:
1 2 3 4 50 5 6
- 1
- 2
- 3
- 4
删除结点
看下面一个双链表:

如何将结点s从链表中删除呢?
原理很简单,首先将结点p的指针域next指向结点s的指针域,也就是p->next = p->next->next,然后将结点q的指针域prior指向结点p,也就是q->prior = p,此时结点p和结点q之间建立起了双向关系,最后释放结点s的内存即可。

看代码如何实现:
int delete_list(PNode pHead,int pos,int *val){
PNode p,q;
int len,i = 0;
len = length_list(pHead);
p = pHead;//初始指向头结点
//判断pos值的合法性
if(pos < 1 || pos > len){
return 0;
}
//找到待删除结点的前一个结点
while(i < pos - 1 && p != NULL){
i++;
p = p->next;
}
//此时p为待删除结点的前一个结点
q = p->next;//q为待删除结点
//保存数据
*val = q->data;
//删除结点
p->next = q->next;
if(p->next!= NULL){
p->next->prior = p;
}
free(q);
return 1;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
这里同样需要考虑删除尾结点的问题,如果要删除的是尾结点,那么尾结点后面已经没有结点了,所以直接后继结点可以不用处理,处理就会报错,我们应该对p的指针域next进行非空判断,千万不要把p->next != NULL写成q != NULL,有些同学想当然地认为,q = p->next,所以if语句里也就写了q != NULL,这样是错误的。因为在判断之前,p的指针域next已经被改变了,只有判断p是否为空,当删除尾结点时,p指向q的指向,而q是尾结点,所以p的指向为NULL,q并不为空,它是尾结点,这是需要注意的一点。
下面是测试代码:
void main(){
PNode pHead;
int a[] = {1,2,3,4,5,6};
int val;
pHead = create_listR(a,6);
traverse_list(pHead);
if(delete_list(pHead,6,&val)){
printf("删除后:\n");
traverse_list(pHead);
printf("删除结点的元素值为:%d\n",val);
}else{
printf("删除失败!\n");
}
getchar();
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
运行结果:
1 2 3 4 5 6
删除后:
1 2 3 4 5
删除结点的元素值为:6
- 1
- 2
- 3
- 4
- 5
至于查找指定元素值的结点位置,或者是查找指定结点位置的元素值,还有链表的销毁,这些操作都与单链表的操作一模一样,也就没有必要重复讲解了。不了解的可以看我的上一篇文章。
课后习题
按照惯例,我同样留下一道算法题:
有一个带头结点的双链表L,试设计一个算法将其所有元素逆置,即第1个元素变为最后一个元素,第2个元素变为倒数第2个元素,……,最后一个元素变为第1个元素。
同样简单分析一下,这道题其实很简单,通过遍历双链表L,然后使用头插法建立链表即可完成,具体如何实现就看大家的了。我会在下一篇专栏文章中揭晓此题答案。
文章来源: blizzawang.blog.csdn.net,作者:·wangweijun,版权归原作者所有,如需转载,请联系作者。
原文链接:blizzawang.blog.csdn.net/article/details/103119537
- 点赞
- 收藏
- 关注作者


评论(0)