👏👏👏

哈喽！大家好，我是【学无止境小奇】，一位热爱分享各种技术的博主！😍😍😍

⭐【学无止境小奇】的创作宗旨：每一条命令都亲自执行过，每一行代码都实际运行过，每一种方法都真实实践过，每一篇文章都良心制作过。✊✊✊

⭐【学无止境小奇】的博客中所有涉及命令、代码的地方，除了提供图片供大家参考，另外会在图片下方提供一份纯文本格式的命令或者代码方便大家粘贴复制直接执行命令或者运行代码。🤝🤝🤝

⭐如果你对技术有着浓厚的兴趣，欢迎关注【学无止境小奇】，欢迎大家和我一起交流。😘😘😘

❤️❤️❤️感谢各位朋友接下来的阅读❤️❤️❤️

一、leetcode算法

1、爬楼梯

1.1、题目

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶
   示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

1.2、思路

思路一：本题是一道经典的算法题，爬楼梯的问题和我们的生活息息相关，我们几乎每天都需要爬楼梯，我们有时会一阶一阶的上，有时赶时间我们会两阶两阶的蹭蹭的上，有时候累了会两阶一阶交叉着上，那么固定的楼梯阶层数我们一共有几种上楼的方式呢？
我们拿到问题以后如果没有思路可以先找找规律，犹如我们数学中给你几个数或者几个图形让你找规律一样，这个时候我们从1阶楼梯开始找共有几种方式，我们发现，1阶楼梯有一种上楼方式，2阶楼梯有两种上楼方式，3阶楼梯有3种上楼方式，4阶楼梯有5中上楼方式，我们这里可以发现每x阶层的上楼方式等于x-1层和x-2层上楼方式的和，这个时候我们就可以根据这种规律来写代码了。

1.3、答案

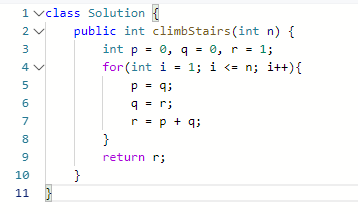
class Solution {
    public int climbStairs(int n) {
        int p = 0, q = 0, r = 1;
        for(int i = 1; i <= n; i++){
            p = q;
            q = r;
            r = p + q;
        }
        return r;
    }
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

复杂度分析

时间复杂度：循环执行 n 次，每次花费常数的时间代价，故渐进时间复杂度为 O(n)。
空间复杂度：这里只用了常数个变量作为辅助空间，故渐进空间复杂度为 O(1)。

文章来源: xiaoqijava.blog.csdn.net，作者：学无止境小奇，版权归原作者所有，如需转载，请联系作者。

原文链接：xiaoqijava.blog.csdn.net/article/details/122977600