HashMap中扩容问题夺命6连问，问到了硬件层，你能顶住吗？

							✨ 我是喜欢分享知识、喜欢写博客的YuShiwen，与大家一起学习，共同成长！
									  📢 闻到有先后，学到了就是自己的，大家加油！
📢 导读：
文章不长，看完后相信你一定会有所收获，本篇文章和一般的面试文章不一样，本篇文章知识点更细、更深，直接到硬件层，更进一步拓宽读者对于计算机的认知，并且还力求知其所以然！
								

  

 

  
1
  
2
  
3
  
4
  
5
 

1.HashMap中扩容为什么是2的n次幂

答：

1. 源码是这样写的，扩容时把当前hash表的数组长度左移一位，即乘以2；
2. 在计算数组下标的时候，还用到了2的n次幂。

2.如何用到了2的n次幂？

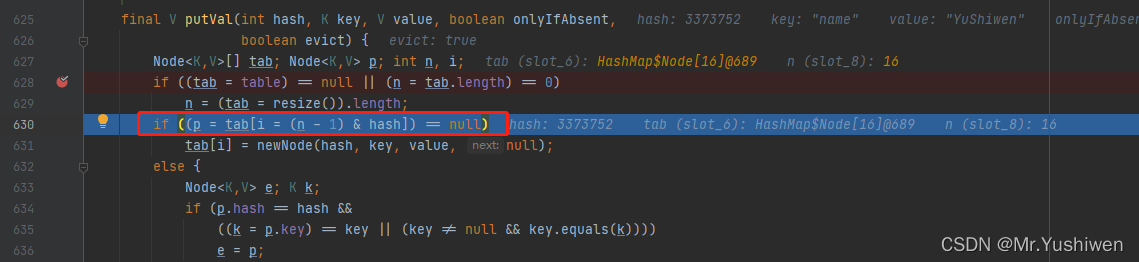
答：在计算数组下标的时候，先把Hash表中数组的长度减1，然后在与key的hash值进行按位与(&)操作.

即i=(n-1)&hash；其中i是tab数组的下标，n是Hash表中数组的长度，hash是key通过hashCode方法计算得到的值，源码如下：

3.如果不是2的n次幂会出现什么情况？

答：我们用反推法证明一下，如果不是2的n次幂，会怎么样，具体内容如下：

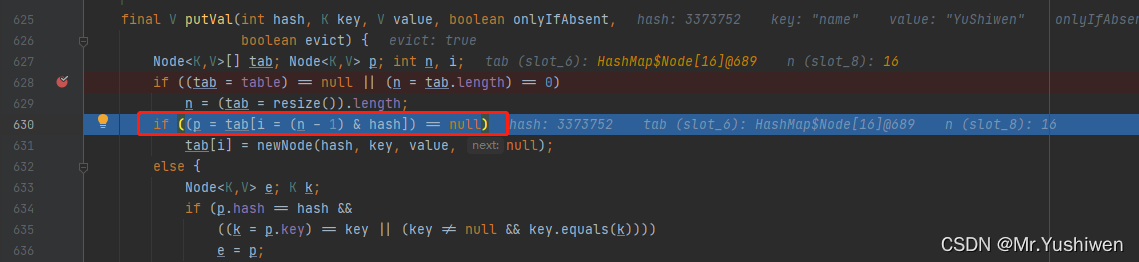
i=(n-1)&hash；其中i是tab数组的下标，n是Hash表中数组的长度，hash是key通过hashCode方法计算得到的值，源码如上：

这里笔者就拿刚开始的扩容量来说，之前是2的n次幂的时候，初始化长度是16，如果不是2的n次幂，我们就举例为13，那么执行上面这段代码的时候，会出现这样的现象：(备注:int类型有32为，为节约空间，这里我只写出低8位，剩下的24位没写出的全是0)

1. 首先13的二进制位0000 1101；
2. 执行n-1，二进制结果为0000 1100；
3. 执行的结果0000 1100与任意的hash进行&操作时，得到的值中第1位和第2位永远是0，即得到的值只能为以下四种可能：
   0000 0000
   0000 0100
   0000 1000
   0000 1100

也就是说初始化长度位13的hash表数组，其中只有下标为0、4、8、12的能存放值，下标为1、2、3、5、6、7、9、10、11是没有用到的，如下图：

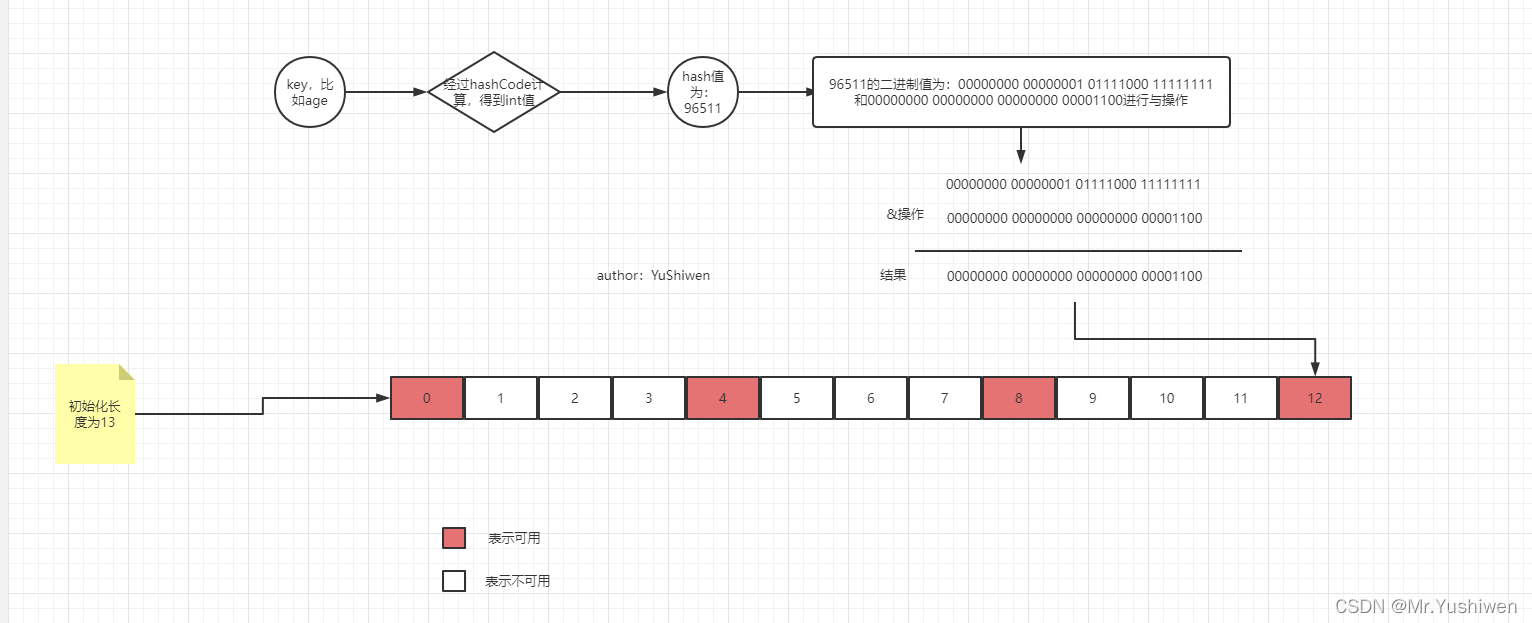
这就会导致让节点成为超长链表的概率大大增加，导致之后的查询时间过长。

如果是2的n次幂，同样的我们执行上述三个步骤：

1. 首先16的二进制位0001 0000；
2. 执行n-1，二进制结果为0000 1111；
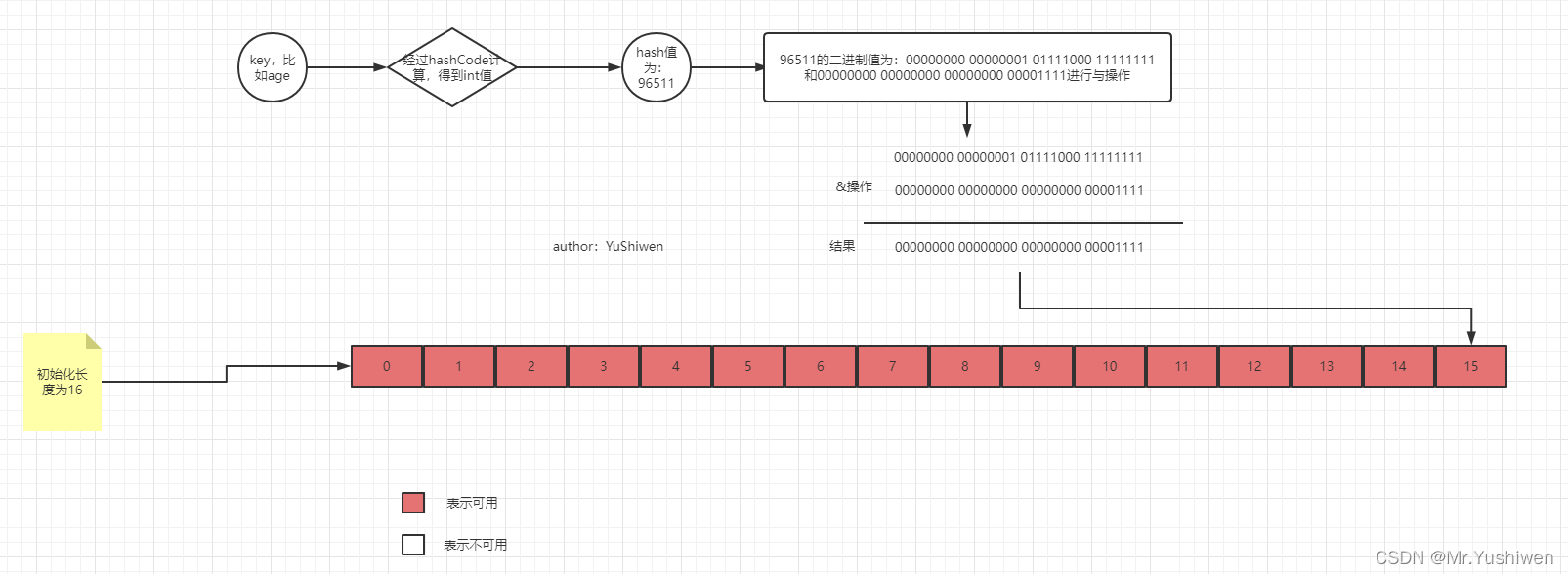
3. 执行的结果0000 1111与任意的hash进行&操作时，得到的值的范围为0-12，包括了数组的全部，也就是说都利用上了。

图就变成了下图：

4.在2中你提到了&(与)操作，为什么HashMap源码里面不用取余或取模来替代&(与)操作?

答：因为取余或取模计算结果有负数，最重要的是在运算速度上，取余或取模操作没有&(与)操作快。

5.那为什么取余或取模计算结果有负数？为什么取余或取模操作没有&(与)操作快？

内心活动：提问者一直在问这个问题，而且都问得这么底层了，这里就不能简单一句话就回答了，想考验我底层功底，那就且听我慢慢道来。

5.1取余或取模计算结果有负数的原因如下：

这里说一下取模Math.floorMod和取余%的区别，在Java中取模的定义如下：

因为取余运算是操作符%，Java中看不到源码，笔者参考数学中对于取余的定义，大致内容如下：

public static int fixMod(int x, int y){
	int r = x - fixDiv(x,y)*y;
	return r;
}

  

 

  
1
  
2
  
3
  
4
 

floorMod调用了floorDiv方法，fixMod调用了fixDiv方法，floorDiv方法和fixDiv都是求商的运算；
其中floorDiv是向负无穷取整，fixDiv是向0取整：

• 当是正数时，比如3/5，floorDiv(商)和fixDiv(商)的值是相同的，都是0；
• 当是负数时，比如-3/5，floorDiv(商)向负无穷取整为-1，fixDiv(商)向0取整为0。

总结就是：

1. 取余，遵循尽可能让商，即fixDiv方法向0靠近的原则；
2. 取模，遵循尽可能让商，即floorDiv方法向负无穷靠近的原则

上面是取余与取模运算其中的一个区别，接下我们看另外一个区别，这个也是重点，我们看一个例子：

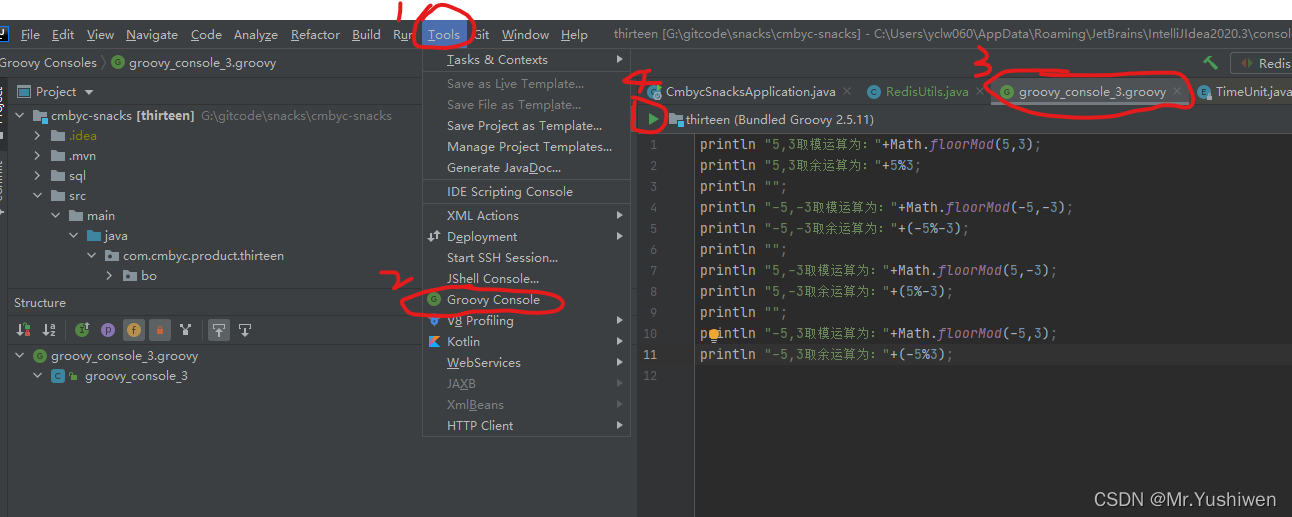
上例代码如下，大家可以自行复制粘贴运行一下康康：

println "5,3取模运算为："+Math.floorMod(5,3);
println "5,3取余运算为："+5%3;
println "";
println "-5,-3取模运算为："+Math.floorMod(-5,-3);
println "-5,-3取余运算为："+(-5%-3);
println "";
println "5,-3取模运算为："+Math.floorMod(5,-3);
println "5,-3取余运算为："+(5%-3);
println "";
println "-5,3取模运算为："+Math.floorMod(-5,3);
println "-5,3取余运算为："+(-5%3);


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
 

运行结果如下：

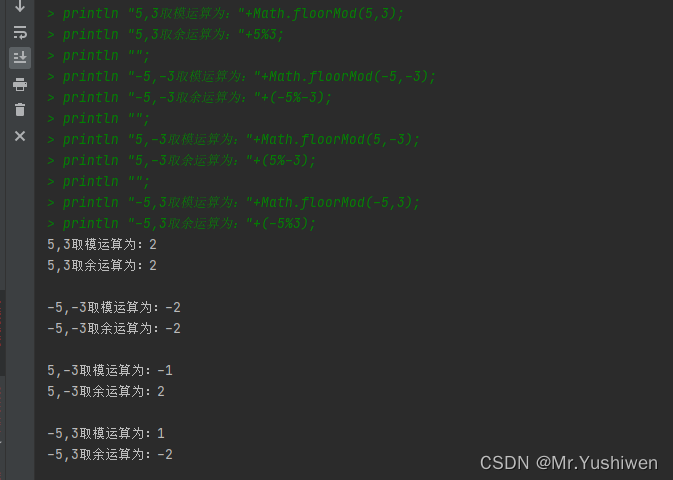
有如下情况：

• 当除数和被除数符号相同时，结果相同；
• 当除数和被除数符号不相同时，有如下两种情况：
  1. 为取模运算时，运算结果的符号和除数相同；
  2. 为取余运算时，运算结果的符号和被除数相同。

通过上面可以可以得知，不论是取模运算还是取余运算，当除数或被除数是负数时，那么计算结果也可能为负数。

5.2取余或取模操作没有&(与)操作快的原因如下：

普通计算器是通过硬件的逻辑运算实现加减乘除的：

从数学上讲，CPU中的ALU在算术上只干了三件事，加法，移位，取反；
在实际的物理电路中，只有与、或、非、异或这四种门电路；
知道了这两点，我们再来分析加减乘除：

1. 加法：逻辑上异或操作，即0与0和1与1为0，0与1和1与0为1，得到本位和的值，根据运算要求，确定是否要进位；
2. 减法：对于计算机来说没有减法，减法是把某一个数看做负数，然后在计算机中用补码存起来（即原码取反加1），然后执行加法运算；（加法也是用的补码计算的）
3. 乘法：移位，逻辑判断，累加；
4. 除法：移位，逻辑判断，累减。

2位加法器门电路大致如下：(这里以两位加法器举例，现实中可以由更多的这些门电路组成更多位的加法器)


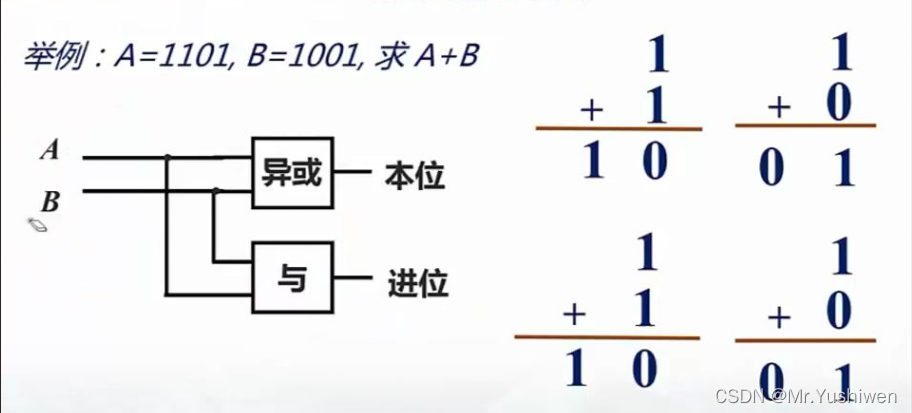
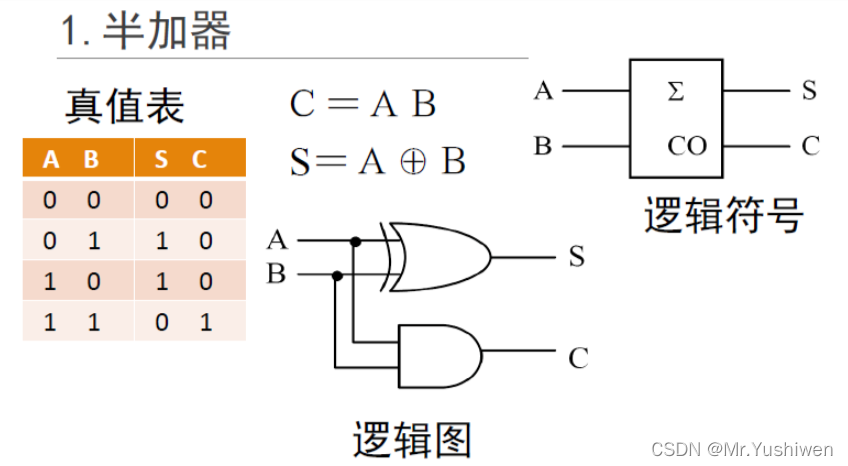
乘法器门电路图如下，乘法器由加法器和与门组成(同样这里也只举例2位*2位的乘法，更高位的门电路更复杂，但是实现的基本方式是没有变化的)

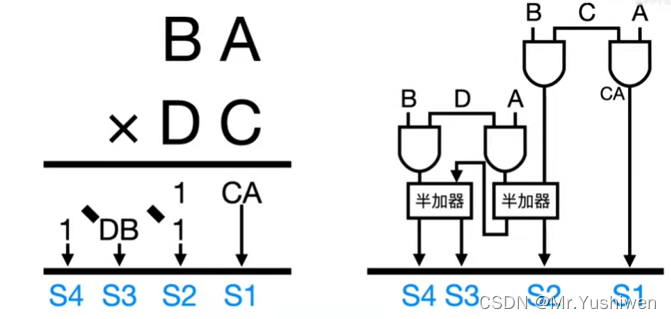
从硬件实现上讲，可以看出，实现这四种基本运算只需要加法器、移位器和基本逻辑门电路硬件组件就行。早期的cpu里结构简单，只有这些组件，没有专门的乘法器、除法器。后来的cpu会集成专门的并行处理电路在cpu内建的协处理器（比如浮点运算器，很早的cpu是没有专门计算浮点的电路的）中，在硬件上实现，这样计算速度就快了。当然，计算的逻辑还是没变。

上面3.1章节中，我们提到过，取模操作如下（取余操作也是类似的）：

r=x-floorDiv(x,y)*y

  

 

  
1
 

在这个关系式中，fixMod它是求商操作，求商操作包含了除法操作，得到的商又和y相乘，上面我们讲到了：
乘法可以拆分为：移位，逻辑判断，累加；
除法可以拆分为：移位，逻辑判断，累减。
可以看到乘法和除法的底层实现就是移位操作还有累加操作，再加上一些逻辑判断，这和&(与)操作相比效率低太多了，与操作只需要一个与门逻辑电路就可以计算完成。

附录：和笔者一起看源码

测试代码（JDK1.8）：
创建一个HashMap，此时为空，首先我们向HashMap中插入key=”name“，value=”YuShiwen“的键值对。

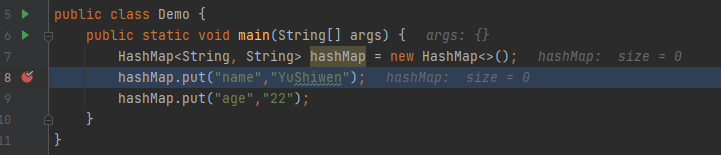
跟进代码中，调用了HashMap中的putVal()方法

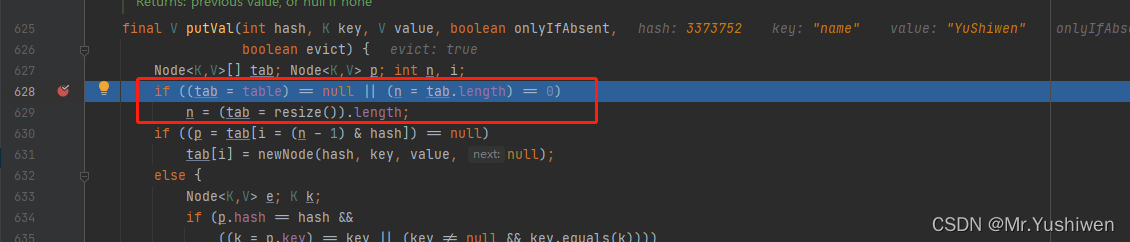
跟进putVal方法中：

1. 第一张截图：刚开始的时候Hash表是空的，即tab是null进入if语句中，调用resize()方法进行初始化，初始化长度为16。（ps：初始化或者扩容的时候会调用resize()方法，扩容的方法为左移一位，即在原来的大小上乘以2）
2. 第二张截图：第一次的时候，在resize()方法中返回默认的大小为16.
   
   

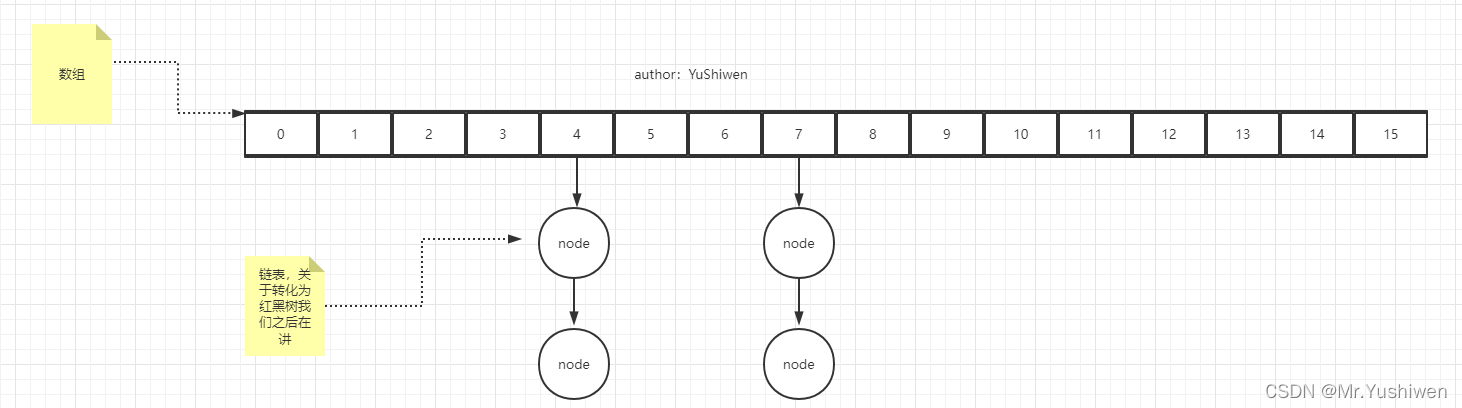
putVal方法返回默认值16后，我们继续看，（此时HashMap表的长度就是16了，即n的值是16；我们都知道HashMap底层的实现是数组+链表，即是如下第一张图的结构；）之后到了一个if语句，该if语句中就是上面提到的计算数组下标的过程，即先把Hash表中数组的长度减1，然后在与key的hash值进行按位与(&)操作。

我是喜欢分享知识、喜欢写博客的YuShiwen，与大家一起学习，共同成长！咋们下篇博文见。

文章来源: blog.csdn.net，作者：Mr.Yushiwen，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/MrYushiwen/article/details/123493489