轻轻松松学递归
概念
程序调用自身的编程技巧称为递归(Recursion)。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说,递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
递归调用机制
我们来看一个案例:
public class RecursionTest {
public static void main(String[] args) {
test(5);
}
public static void test(int num) {
if (num > 2) {
test(num - 1);
}
System.out.println("num = " + num);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
若是你能在考虑片刻后得到结果,说明递归的基本思想你还没有忘记。
递归的调用规则:当程序执行到一个方法时,就会在栈中开辟一个独立的空间。

运行过程如果所示,需要注意的是,在每次递归调用的过程中,都回去栈中开辟独立的空间,而每个空间中的变量是独立的,互不影响的。而我们知道,栈结构是先进后出的,所以此时会先从test(2)开始从上往下执行,最后的执行结果则为:
n = 2
n = 3
n = 4
n = 5
- 1
- 2
- 3
- 4
递归规则
通过递归能够帮助我们解决实际开发中的很多问题。
You have several identical balls that you wish to place in several baskets. Each basket has the same maximum capacity. You are given an int baskets, the number of baskets you have. You are given an int capacity, the maximum capacity of each basket. Finally you are given an int balls, the number of balls to sort into baskets. Return the number of ways you can divide the balls into baskets. If this cannot be done without exceeding the capacity of the baskets, return 0.
Each basket is distinct, but all balls are identical. Thus, if you have two balls to place into two baskets, you could have (0, 2), (1, 1), or (2, 0), so there would be three ways to do this.
这是一道Google的编程大赛题目,题目意思是:
你有几个相同的球,你希望放在几个篮子里。每个篮子都有相同的最大容量。给出一个int型的baskets,代表篮子的数量。给出一个int型的capacity,代表每个篮子的最大容量。最后,给出int型的balls,表示归类到篮子里的球的数量。返回值是把球归类到篮子里的方式的数量。如果这不能在不超过篮子容量的情况下完成,返回0。
每个篮子是不同的,但所有的球是相同的。因此,如果你有两个球要放到两个篮子里,你可以有(0,2)(1,1)或(2,0)三种方法。
这道题就能通过递归来完美地解决,但在这里不对该题作专门讲解。
从上面来看,我们需要知道递归必须遵守的规则:
- 执行一个方法时,就会在栈中创建一个新的受保护的独立空间
- 方法的局部变量是独立的,互不影响的
- 如果方法中使用的是引用类型变量(比如数组),就会共享该引用类型的数据
- 递归必须向退出退出递归的条件逼近,否则就是无限递归
- 当一个方法执行完毕,或者遇到return时,就会返回,遵守谁调用,就将结果返回谁的规则。同时,当方法执行完毕或返回时,该方法也就执行完毕
迷宫回溯问题
对于递归有了一个简单的复习了解之后,我们用递归来解决一些编程中的经典问题,我们先看一个迷宫回溯问题。
迷宫回溯问题说的是:
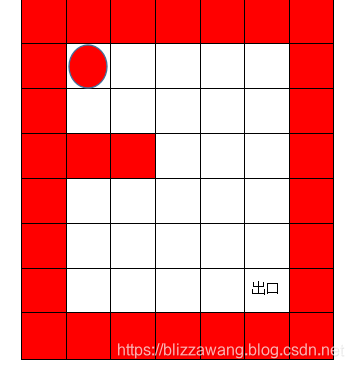
在这样的一个迷宫中,红色代表墙壁,现在有一个红色的小球,要求从开始位置出发,解出到出口位置的最短路径。
要想解决这样一个问题,我们首先得制定一个策略,决定小球的行走顺序,我们规定:
先走下面,倘若下面走不通,就走右面;倘若右面走不通,就走上面;倘若上面走不通,就走左面。
你们在具体实现的时候不需要和我的策略一样,这只是一种解题方式。
代码如下:
public class MazeBack {
public static void main(String[] args) {
// 创建一个二维数组,模拟迷宫
int[][] map = new int[8][7];
// 约定1为墙壁
// 上下置为1
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
// 左右置为1
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
map[3][1] = 1;
map[3][2] = 1;
System.out.println("原始地图:");
for (int[] temp : map) {
for (Integer i : temp) {
System.out.print(i + " ");
}
System.out.println();
}
//递归寻找路径
findWay(map, 1, 1);
System.out.println("小球行走路径:");
for (int[] temp : map) {
for (Integer i : temp) {
System.out.print(i + " ");
}
System.out.println();
}
}
/**
* 使用递归求出迷宫路径 如果小球能够到map[6][5],则证明找到正确路径
* 我们约定当map[i][j]为0表示墙,为1表示当前位置没有走过,为2表示当前位置可以走通,为3表示当前位置已经走过,但走不通
*
* @param map 地图
* @param i 出发点
* @param j 出发点
* @return 如果找到正确路径,返回true,否则返回false
*/
public static boolean findWay(int[][] map, int i, int j) {
if (map[6][5] == 2) {
// 此时说明路径已经找到
return true;
} else {
if (map[i][j] == 0) {
// 此时说明当前位置还没有走过
// 按照策略走
map[i][j] = 2;// 假设这个位置是可以走通的
if (findWay(map, i + 1, j)) {// 在该点的基础上向下走
return true;
} else if (findWay(map, i, j + 1)) {// 在该点的基础上向右走
return true;
} else if (findWay(map, i - 1, j)) {// 在该点的基础上向上走
return true;
} else if (findWay(map, i, j - 1)) {// 在该点的基础上向左走
return true;
} else {
// 此时说明map[i][j]是走不通的
map[i][j] = 3;// 将map[i][j]置为3
return false;
}
} else {
// 如果map[i][j]不为0,它还有可能为1、2和3
return false;
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
运行结果:
原始地图:
1 1 1 1 1 1 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 1 1 1 1
小球行走路径:
1 1 1 1 1 1 1
1 2 0 0 0 0 1
1 2 2 2 0 0 1
1 1 1 2 0 0 1
1 0 0 2 0 0 1
1 0 0 2 0 0 1
1 0 0 2 2 2 1
1 1 1 1 1 1 1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
数字2所表示的位置则形成了一条正确的行走路径。
这个程序有一定的难度,需要一定的时间消化,我们一起来分析一下,帮助理解:
首先小球起点为[1][1],那么就会进入else分支,那么首先我们就假设小球所在的位置是可以走通的,所以将其值置为2,然后我们在该位置的基础上按照我们的策略,即:下→右→上→左的方式进行摸索,所以将i+1,j作为出发点调用其自身,作递归处理,步骤和前面相同。
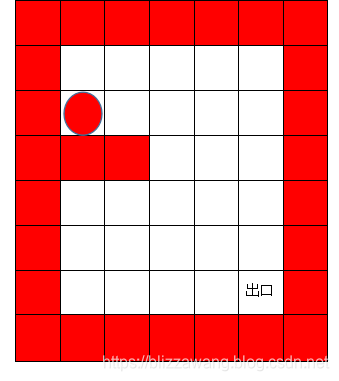
此时在向下摸索的过程中发现,下面的位置是走不通的,因为是墙,所以它会向右继续摸索,那么当然又是递归调用,将i,j+1作为出发点调用其自身。
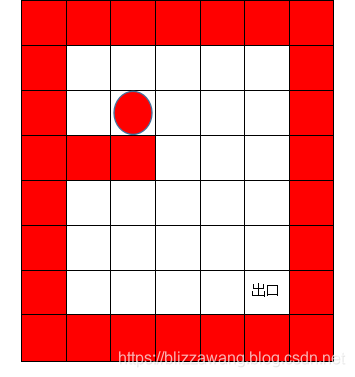
小球在该位置继续向下摸索,发现走不通,就向右摸索,发现能走通,就继续走,然后又向下摸索,依次类推,直至走到出口,所以小球行走路径为:
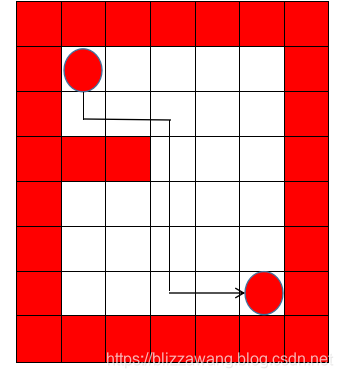
有细心的人可能就发现了,在这个程序中并没有回溯啊,确实,因为这个迷宫相对简单,在寻找的过程中并没有出现回溯,而是能很顺利地依次执行。
我们来看一个极端的情况:

假设是这样的一个情况,我们把小球直接堵死,也就是让
map[1][2] = 1;
map[2][2] = 1;
- 1
- 2
我们再来运行刚才的程序,结果为:
原始地图:
1 1 1 1 1 1 1
1 0 1 0 0 0 1
1 0 1 0 0 0 1
1 1 1 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 1 1 1 1
小球行走路径:
1 1 1 1 1 1 1
1 3 1 0 0 0 1
1 3 1 0 0 0 1
1 1 1 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 1 1 1 1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
可以看到,小球行走路径中出现了数字3,这说明在这次的路径寻找过程中是出现了回溯的。因为在小球起点往下走了之后,它发现下面走不通,右面走不通,上面走过了,左面也走不通,此时认为该位置已经走过但是走不通,所以将其值置为3。此时程序会返回,返回到上一次的位置(即起点),也就是回溯了,然后继续摸索,发现仍然走不通,所以将该位置也置为3。
上面只是简单实现了迷宫的路径寻找问题,接下来我们来看看如何寻找迷宫中的最短路径。
寻找迷宫中的最短路径思想非常简单,即改变摸索策略,例如我们将摸索策略由下→右→上→左改为上→右→下→左,此时代码修改为:
public static boolean findWay(int[][] map, int i, int j) {
if (map[6][5] == 2) {
return true;
} else {
if (map[i][j] == 0) {
map[i][j] = 2;
if (findWay(map, i - 1, j)) {// 在该点的基础上向上走
return true;
} else if (findWay(map, i, j + 1)) {// 在该点的基础上向右走
return true;
} else if (findWay(map, i + 1, j)) {// 在该点的基础上向下走
return true;
} else if (findWay(map, i, j - 1)) {// 在该点的基础上向左走
return true;
} else {
map[i][j] = 3;// 将map[i][j]置为3
return false;
}
} else {
return false;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
然后运行程序,结果为:
原始地图:
1 1 1 1 1 1 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 1 1 1 1
小球行走路径:
1 1 1 1 1 1 1
1 2 2 2 2 2 1
1 0 0 0 0 2 1
1 1 1 0 0 2 1
1 0 0 0 0 2 1
1 0 0 0 0 2 1
1 0 0 0 0 2 1
1 1 1 1 1 1 1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
这样小球的行走路径也会相应的变化,我们只需要得出每个策略的行走路径,并用数组将每个策略得到的数值2记录下来,最后比较一下数组中哪个包含数值2最少,其对应的路径即为最短路径。
八皇后问题
看完迷宫回溯问题之后,可能有些人会有点懵,所以,这里我再讲解一个比较经典的递归问题,希望大家能够更快掌握递归。
八皇后问题是一个古老而著名的问题,是回溯算法的典型案例。该问题是国际西洋棋手马克斯·贝瑟尔于1848年提出。说的是在8X8格的国际象棋棋盘上摆放八个皇后,使其不能相互攻击,即:任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
我们先来玩一个游戏,了解一下八皇后问题:

这是一个错误示范,即两个皇后不允许处于同一行、同一列或同一斜线。
接下来我们看一个正确摆法:

通过这个游戏我们不难理解八皇后问题的规则,接下来我们分析一下八皇后问题的算法思路:
- 第一个皇后先放第一行或第一列
- 第二个皇后放在第二行第一列,然后能否放置,如果不能,就放在第二列,继续判断,若不能放置,则放在第三列,以此类推,直至找到合适的位置
- 第三个皇后也按第二步骤不断寻找,第四个皇后也如此,直至第八个皇后也找到了一个与其它皇后不冲突的地方,此时找到了一个正确解
- 当得到一个正确解之后,在栈回退到上一个栈时,就会开始回溯,即:将第一个皇后,放到第一列的所有正确解全部得到
- 然后第一个皇后放到第二列,后面重复执行1、2、3、4步骤
需要知道的是,在回溯的时候,我们是从最后一个皇后开始,不断地寻找不和其它皇后冲突的位置,当回溯完成后,即找到了第一个皇后放在第一列的所有解。
代码如下:
public class EightQueue {
//定义一个max表示共有多少个皇后
int max = 8;
//定义数组array, 保存皇后放置位置的结果,比如 arr = {0 , 4, 7, 5, 2, 6, 1, 3}
int[] array = new int[max];
static int count = 0;
static int judgeCount = 0;
public static void main(String[] args) {
EightQueue queue8 = new EightQueue();
queue8.check(0);
System.out.printf("一共有%d解法", count);
System.out.printf("一共判断冲突的次数%d次", judgeCount); //
}
//编写一个方法,放置第n个皇后
//特别注意: check 是 每一次递归时,进入到check中都有 for(int i = 0; i < max; i++),因此会有回溯
private void check(int n) {
if(n == max) { //n = 8 , 八个皇后已放置完毕
print();
return;
}
//依次放入皇后,并判断是否冲突
for(int i = 0; i < max; i++) {
//先把当前这个皇后 n , 放到该行的第1列
array[n] = i;
//判断当放置第n个皇后到i列时,是否冲突
if(judge(n)) { // 不冲突
//接着放n+1个皇后,即开始递归
check(n+1); //
}
//如果冲突,就继续执行 array[n] = i; 即将第n个皇后,放置在本行的后一个位置
}
}
//查看当我们放置第n个皇后, 就去检测该皇后是否和前面已经摆放的皇后冲突
/**
*
* @param n 表示第n个皇后
* @return
*/
private boolean judge(int n) {
judgeCount++;
for(int i = 0; i < n; i++) {
// 说明
//1. array[i] == array[n] 表示判断 第n个皇后是否和前面的n-1个皇后在同一列
//2. Math.abs(n-i) == Math.abs(array[n] - array[i]) 表示判断第n个皇后是否和第i皇后是否在同一斜线
// n = 1 放置第 2列 1 n = 1 array[1] = 1
// Math.abs(1-0) == 1 Math.abs(array[n] - array[i]) = Math.abs(1-0) = 1
//3. 判断是否在同一行, 没有必要,n 每次都在递增
if(array[i] == array[n] || Math.abs(n-i) == Math.abs(array[n] - array[i]) ) {
return false;
}
}
return true;
}
//写一个方法,可以将皇后摆放的位置输出
private void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
运行结果为:
0 4 7 5 2 6 1 3
0 5 7 2 6 3 1 4
0 6 3 5 7 1 4 2
0 6 4 7 1 3 5 2
1 3 5 7 2 0 6 4
1 4 6 0 2 7 5 3
1 4 6 3 0 7 5 2
1 5 0 6 3 7 2 4
1 5 7 2 0 3 6 4
1 6 2 5 7 4 0 3
1 6 4 7 0 3 5 2
1 7 5 0 2 4 6 3
2 0 6 4 7 1 3 5
2 4 1 7 0 6 3 5
2 4 1 7 5 3 6 0
2 4 6 0 3 1 7 5
2 4 7 3 0 6 1 5
2 5 1 4 7 0 6 3
2 5 1 6 0 3 7 4
2 5 1 6 4 0 7 3
2 5 3 0 7 4 6 1
2 5 3 1 7 4 6 0
2 5 7 0 3 6 4 1
2 5 7 0 4 6 1 3
2 5 7 1 3 0 6 4
2 6 1 7 4 0 3 5
2 6 1 7 5 3 0 4
2 7 3 6 0 5 1 4
3 0 4 7 1 6 2 5
3 0 4 7 5 2 6 1
3 1 4 7 5 0 2 6
3 1 6 2 5 7 0 4
3 1 6 2 5 7 4 0
3 1 6 4 0 7 5 2
3 1 7 4 6 0 2 5
3 1 7 5 0 2 4 6
3 5 0 4 1 7 2 6
3 5 7 1 6 0 2 4
3 5 7 2 0 6 4 1
3 6 0 7 4 1 5 2
3 6 2 7 1 4 0 5
3 6 4 1 5 0 2 7
3 6 4 2 0 5 7 1
3 7 0 2 5 1 6 4
3 7 0 4 6 1 5 2
3 7 4 2 0 6 1 5
4 0 3 5 7 1 6 2
4 0 7 3 1 6 2 5
4 0 7 5 2 6 1 3
4 1 3 5 7 2 0 6
4 1 3 6 2 7 5 0
4 1 5 0 6 3 7 2
4 1 7 0 3 6 2 5
4 2 0 5 7 1 3 6
4 2 0 6 1 7 5 3
4 2 7 3 6 0 5 1
4 6 0 2 7 5 3 1
4 6 0 3 1 7 5 2
4 6 1 3 7 0 2 5
4 6 1 5 2 0 3 7
4 6 1 5 2 0 7 3
4 6 3 0 2 7 5 1
4 7 3 0 2 5 1 6
4 7 3 0 6 1 5 2
5 0 4 1 7 2 6 3
5 1 6 0 2 4 7 3
5 1 6 0 3 7 4 2
5 2 0 6 4 7 1 3
5 2 0 7 3 1 6 4
5 2 0 7 4 1 3 6
5 2 4 6 0 3 1 7
5 2 4 7 0 3 1 6
5 2 6 1 3 7 0 4
5 2 6 1 7 4 0 3
5 2 6 3 0 7 1 4
5 3 0 4 7 1 6 2
5 3 1 7 4 6 0 2
5 3 6 0 2 4 1 7
5 3 6 0 7 1 4 2
5 7 1 3 0 6 4 2
6 0 2 7 5 3 1 4
6 1 3 0 7 4 2 5
6 1 5 2 0 3 7 4
6 2 0 5 7 4 1 3
6 2 7 1 4 0 5 3
6 3 1 4 7 0 2 5
6 3 1 7 5 0 2 4
6 4 2 0 5 7 1 3
7 1 3 0 6 4 2 5
7 1 4 2 0 6 3 5
7 2 0 5 1 4 6 3
7 3 0 2 5 1 6 4
一共有92解法一共判断冲突的次数15720次
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
从运行结果也可以看出,它先将第一个皇后在第一列放置的所有解得到,然后获得第二列,接着第三列,直至最后一列。
理论上应该创建一个二维数组表示棋盘,但是实际上也可以通过算法,用一个一维数组来表示。例如:arr[8] = {0,4,7,5,2,6,1,3},其中arr[i] = value,value表示第i+1个皇后放在第i+1行的第value+1列。
这样,关于八皇后问题的算法实现也就完成了,算法思想会有点绕,要理解确实有难度。
递归的缺点
从八皇后问题可以知道,一个8X8的棋盘,解决冲突的次数就高达一万多次,所以递归也是有很大缺陷的,具体缺点如下:
-
递归由于是函数调用自身,而函数调用是有时间和空间的消耗的:每一次函数调用,都需要在栈中分配空间
-
递归中有很多重复进行的计算,由于其本质是把一个问题分解成两个或者多个小问题,多个小问题存在相互重叠的部分
-
递归经常会出现栈溢出问题,因为每一次方法的调用都会在栈中分配空间,而每个进程的栈的容量是有限的,当调用的层次太多时,就会超出栈的容量,从而导致栈溢出
文章来源: blizzawang.blog.csdn.net,作者:·wangweijun,版权归原作者所有,如需转载,请联系作者。
原文链接:blizzawang.blog.csdn.net/article/details/100555894
- 点赞
- 收藏
- 关注作者


评论(0)