查找算法之顺序查找,折半查找,二叉查找树
查找表的概念
查找表是由同一类型的数据元素构成的集合。例如电话号码簿和字典都可以看作是一张查找表。
在查找表中只做查找操作,而不改动表中数据元素,称此类查找表为静态查找表;反之,在查找表中做查找操作的同时进行插入数据或者删除数据的操作,称此类表为动态查找表。
顺序查找
顺序查找的查找过程为:从表中的最后一个数据元素开始,逐个同记录的关键字做比较,如果匹配成功,则查找成功;反之,如果直到表中第一个关键字查找完也没有成功匹配,则查找失败
同时,在程序中初始化创建查找表时,由于是顺序存储,所以将所有的数据元素存储在数组中,但是把第一个位置留给了用户用于查找的关键字。例如,在顺序表{1,2,3,4,5,6}中查找数据元素值为 7 的元素,则添加后的顺序表为:

图1
顺序表的一端添加用户用于搜索的关键字,称作“监视哨”。
图 1 中监视哨的位置也可放在数据元素 6 的后面(这种情况下,整个查找的顺序应有逆向查找改为顺序查找)。
放置好监视哨之后,顺序表遍历从没有监视哨的一端依次进行,如果查找表中有用户需要的数据,则程序输出该位置;反之,程序会运行至监视哨,此时匹配成功,程序停止运行,但是结果是查找失败。
代码实现:
/*
* @Description: 顺序查找算法
* @Version: V1.0
* @Autor: Carlos
* @Date: 2020-05-22 15:52:11
* @LastEditors: Carlos
* @LastEditTime: 2020-06-03 16:56:06
*/
#include <stdio.h>
#include <stdlib.h>
#define keyType int
typedef struct {
//查找表中每个数据元素的值
keyType key;
//如果需要,还可以添加其他属性
}ElemType;
typedef struct{
//存放查找表中数据元素的数组
ElemType *elem;
//记录查找表中数据的总数量
int length;
}SSTable;
/**
* @Description: 创建查找表
* @Param: SSTable **st 指向结构体指针的指针,即指针变量的指针,int length 创建的二叉树的长度
* @Return: 无
* @Author: Carlos
*/
void Create(SSTable **st,int length){
(*st)=(SSTable*)malloc(sizeof(SSTable));
(*st)->length=length;
//结构体指针分配空间
(*st)->elem =(ElemType*)malloc((length+1)*sizeof(ElemType));
printf("输入表中的数据元素:\n");
//根据查找表中数据元素的总长度,在存储时,从数组下标为 1 的空间开始存储数据
for (int i=1; i<=length; i++) {
scanf("%d",&((*st)->elem[i].key));
}
}
/**
* @Description: 查找表查找的功能函数,其中key为关键字
* @Param: SSTable *st指向结构体变量的指针,keyType key 要查找的元素
* @Return: key在查找表中的位置
* @Author: Carlos
*/
int Search_seq(SSTable *st,keyType key){
//将关键字作为一个数据元素存放到查找表的第一个位置,起监视哨的作用
st->elem[0].key=key;
int i=st->length;
//从查找表的最后一个数据元素依次遍历,一直遍历到数组下标为0
while (st->elem[i].key!=key) {
i--;
}
//如果 i=0,说明查找失败;反之,返回的是含有关键字key的数据元素在查找表中的位置
return i;
}
int main(int argc, const char * argv[]) {
SSTable *st;
Create(&st, 6);
getchar();
printf("请输入查找数据的关键字:\n");
int key;
scanf("%d",&key);
int location=Search_seq(st, key);
if (location==0) {
printf("查找失败");
}else{
printf("数据在查找表中的位置为:%d",location);
}
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
本文链接:https://blog.csdn.net/qq_16933601/article/details/106500778
折半查找
折半查找,也称二分查找,在某些情况下相比于顺序查找,使用折半查找算法的效率更高。但是该算法的使用的前提是静态查找表中的数据必须是有序的。
例如,在{5,21,13,19,37,75,56,64,88 ,80,92}这个查找表使用折半查找算法查找数据之前,需要首先对该表中的数据按照所查的关键字进行排序:{5,13,19,21,37,56,64,75,80,88,92}。
在折半查找之前对查找表按照所查的关键字进行排序的意思是:若查找表中存储的数据元素含有多个关键字时,使用哪种关键字做折半查找,就需要提前以该关键字对所有数据进行排序。
折半查找算法
对静态查找表{5,13,19,21,37,56,64,75,80,88,92}采用折半查找算法查找关键字为 21 的过程为:
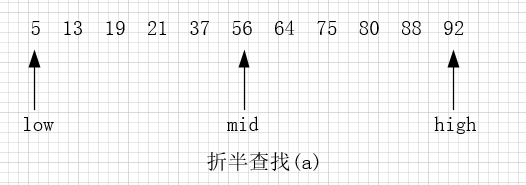
图2
后一个关键字,指针 mid 指向处于 low 和 high 指针中间位置的关键字。在查找的过程中每次都同 mid 指向的关键字进行比较,由于整个表中的数据是有序的,因此在比较之后就可以知道要查找的关键字的大致位置。
例如在查找关键字 21 时,首先同 56 作比较,由于21 < 56,而且这个查找表是按照升序进行排序的,所以可以判定如果静态查找表中有 21 这个关键字,就一定存在于 low 和 mid 指向的区域中间。
因此,再次遍历时需要更新 high 指针和 mid 指针的位置,令 high 指针移动到 mid 指针的左侧一个位置上,同时令 mid 重新指向 low 指针和 high 指针的中间位置。如图3所示:
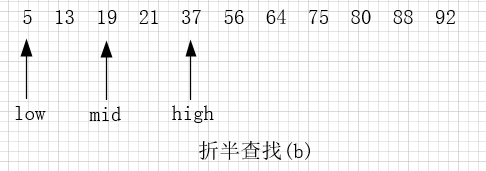
图3
同样,用 21 同 mid 指针指向的 19 作比较,19 < 21,所以可以判定 21 如果存在,肯定处于 mid 和 high 指向的区域中。所以令 low 指向 mid 右侧一个位置上,同时更新 mid 的位置。

图4
当第三次做判断时,发现 mid 就是关键字 21 ,查找结束。
注意:在做查找的过程中,如果 low 指针和 high 指针的中间位置在计算时位于两个关键字中间,即求得 mid 的位置不是整数,需要统一做取整操作。
折半查找的实现代码:
/*
* @Description: 折半查找.前提是静态查找表中的数据必须是有序的。
* @Version: V1.0
* @Autor: Carlos
* @Date: 2020-05-22 16:09:01
* @LastEditors: Carlos
* @LastEditTime: 2020-06-03 16:58:14
*/
#include <stdio.h>
#include <stdlib.h>
#define keyType int
typedef struct {
//查找表中每个数据元素的值
keyType key;
//如果需要,还可以添加其他属性
}ElemType;
typedef struct{
//存放查找表中数据元素的数组
ElemType *elem;
//记录查找表中数据的总数量
int length;
}SSTable;
/**
* @Description: 创建查找表
* @Param: SSTable **st 指向结构体指针的指针,即指针变量的指针,int length 创建的二叉树的长度
* @Return: 无
* @Author: Carlos
*/
void Create(SSTable **st,int length){
(*st)=(SSTable*)malloc(sizeof(SSTable));
(*st)->length=length;
(*st)->elem = (ElemType*)malloc((length+1)*sizeof(ElemType));
printf("输入表中的数据元素:\n");
//根据查找表中数据元素的总长度,在存储时,从数组下标为 1 的空间开始存储数据
for (int i=1; i<=length; i++) {
scanf("%d",&((*st)->elem[i].key));
}
}
//折半查找算法
/**
* @Description: 折半查找算法
* @Param: SSTable *ST 指向结构体的指针,keyType key 要插入的元素
* @Return: 成功的返回key在查找表中的位置,否则返回0
* @Author: Carlos
*/
int Search_Bin(SSTable *ST,keyType key){
//初始状态 low 指针指向第一个关键字
int low=1;
//high 指向最后一个关键字
int high=ST->length;
int mid;
while (low<=high) {
//int 本身为整形,所以,mid 每次为取整的整数
mid=(low+high)/2;
//如果 mid 指向的同要查找的相等,返回 mid 所指向的位置
if (ST->elem[mid].key==key)
{
return mid;
}
//如果mid指向的关键字较大,则更新 high 指针的位置
else if(ST->elem[mid].key>key)
{
high=mid-1;
}
//反之,则更新 low 指针的位置
else{
low=mid+1;
}
}
return 0;
}
int main(int argc, const char * argv[]) {
SSTable *st;
Create(&st, 11);
getchar();
printf("请输入查找数据的关键字:\n");
int key;
scanf("%d",&key);
int location=Search_Bin(st, key);
//如果返回值为 0,则证明查找表中未查到 key 值,
if (location==0) {
printf("查找表中无该元素");
}else{
printf("数据在查找表中的位置为:%d",location);
}
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
二叉查找树
动态查找表中做查找操作时,若查找成功可以对其进行删除;如果查找失败,即表中无该关键字,可以将该关键字插入到表中。
动态查找表的表示方式有多种,本节介绍一种使用树结构表示动态查找表的实现方法——二叉排序树(又称为“二叉查找树”)。
二叉查找树概念
二叉排序树要么是空二叉树,要么具有如下特点:
- 二叉排序树中,如果其根结点有左子树,那么左子树上所有结点的值都小于根结点的值;
- 二叉排序树中,如果其根结点有右子树,那么右子树上所有结点的值都大小根结点的值;
- 二叉排序树的左右子树也要求都是二叉排序树;
例如,图 5 就是一个二叉排序树:

图5
使用二叉排序树查找关键字
二叉排序树中查找某关键字时,查找过程类似于次优二叉树,在二叉排序树不为空树的前提下,首先将被查找值同树的根结点进行比较,会有 3 种不同的结果:
- 如果相等,查找成功;
- 如果比较结果为根结点的关键字值较大,则说明该关键字可能存在其左子树中;
- 如果比较结果为根结点的关键字值较小,则说明该关键字可能存在其右子树中;
实现函数为:(运用递归的方法)
/**
* @Description: 二叉排序树查找算法
* @Param: BiTree T KeyType key BiTree f BiTree *p
* @Return: 删除成功 TRUE 删除失败 FALSE
* @Author: Carlos
*/
int SearchBST(BiTree T, KeyType key, BiTree f, BiTree *p)
{
//如果 T 指针为空,说明查找失败,令 p 指针指向查找过程中最后一个叶子结点,并返回查找失败的信息
if (!T)
{
*p = f;
return FALSE;
}
//如果相等,令 p 指针指向该关键字,并返回查找成功信息
else if (key == T->data)
{
*p = T;
return TRUE;
}
//如果 key 值比 T 根结点的值小,则查找其左子树;反之,查找其右子树
else if (key < T->data)
{
return SearchBST(T->lchild, key, T, p);
}
else
{
return SearchBST(T->rchild, key, T, p);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
二叉排序树中插入关键字
二叉排序树本身是动态查找表的一种表示形式,有时会在查找过程中插入或者删除表中元素,当因为查找失败而需要插入数据元素时,该数据元素的插入位置一定位于二叉排序树的叶子结点,并且一定是查找失败时访问的最后一个结点的左孩子或者右孩子。
例如,在图 1 的二叉排序树中做查找关键字 1 的操作,当查找到关键字 3 所在的叶子结点时,判断出表中没有该关键字,此时关键字 1 的插入位置为关键字 3 的左孩子。
所以,二叉排序树表示动态查找表做插入操作,只需要稍微更改一下上面的代码就可以实现,具体实现代码为:
/**
* @Description: 二叉排序树查找算法
* @Param: BiTree T KeyType key BiTree f BiTree *p
* @Return: 删除成功 TRUE 删除失败 FALSE
* @Author: Carlos
*/
int SearchBST(BiTree T, KeyType key, BiTree f, BiTree *p)
{
//如果 T 指针为空,说明查找失败,令 p 指针指向查找过程中最后一个叶子结点,并返回查找失败的信息
if (!T)
{
*p = f;
return FALSE;
}
//如果相等,令 p 指针指向该关键字,并返回查找成功信息
else if (key == T->data)
{
*p = T;
return TRUE;
}
//如果 key 值比 T 根结点的值小,则查找其左子树;反之,查找其右子树
else if (key < T->data)
{
return SearchBST(T->lchild, key, T, p);
}
else
{
return SearchBST(T->rchild, key, T, p);
}
}
/**
* @Description: 二叉树插入函数
* @Param: BiTree *T 二叉树结构体指针的指针 ElemType e 要插入的元素
* @Return: 删除成功 TRUE 删除失败 FALSE
* @Author: Carlos
*/
int InsertBST(BiTree *T, ElemType e)
{
BiTree p = NULL;
//如果查找不成功,需做插入操作
if (!SearchBST((*T), e, NULL, &p))
{
//初始化插入结点
BiTree s = (BiTree)malloc(sizeof(BiTree));
s->data = e;
s->lchild = s->rchild = NULL;
//如果 p 为NULL,说明该二叉排序树为空树,此时插入的结点为整棵树的根结点
if (!p)
{
*T = s;
}
//如果 p 不为 NULL,则 p 指向的为查找失败的最后一个叶子结点,只需要通过比较 p 和 e 的值确定 s 到底是 p 的左孩子还是右孩子
else if (e < p->data)
{
p->lchild = s;
}
else
{
p->rchild = s;
}
return TRUE;
}
//如果查找成功,不需要做插入操作,插入失败
return FALSE;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
通过使用二叉排序树对动态查找表做查找和插入的操作,同时在中序遍历二叉排序树时,可以得到有关所有关键字的一个有序的序列。
例如,假设原二叉排序树为空树,在对动态查找表 {3,5,7,2,1} 做查找以及插入操作时,可以构建出一个含有表中所有关键字的二叉排序树,过程如图6 所示:

图6
通过不断的查找和插入操作,最终构建的二叉排序树如图 6(5) 所示。当使用中序遍历算法遍历二叉排序树时,得到的序列为:1 2 3 5 7 ,为有序序列。
一个无序序列可以通过构建一棵二叉排序树,从而变成一个有序序列。
二叉排序树中删除关键字
在查找过程中,如果在使用二叉排序树表示的动态查找表中删除某个数据元素时,需要在成功删除该结点的同时,依旧使这棵树为二叉排序树。
假设要删除的为结点 p,则对于二叉排序树来说,需要根据结点 p 所在不同的位置作不同的操作,有以下 3 种可能:
- 结点 p 为叶子结点,此时只需要删除该结点,并修改其双亲结点的指针即可;
- 结点 p 只有左子树或者只有右子树,此时只需要将其左子树或者右子树直接变为结点 p 双亲结点的左子树即可;
- 结点 p 左右子树都有,此时有两种处理方式:
(1).令结点 p 的左子树为其双亲结点的左子树;结点 p 的右子树为其自身直接前驱结点的右子树,如图7所示;

图7
(2)用结点 p 的直接前驱(或直接后继)来代替结点 p,同时在二叉排序树中对其直接前驱(或直接后继)做删除操作。如图 8 为使用直接前驱代替结点 p:

图8
图 8中,在对左图进行中序遍历时,得到的结点 p 的直接前驱结点为结点 s,所以直接用结点 s 覆盖结点 p,由于结点 s 还有左孩子,根据第 2 条规则,直接将其变为双亲结点的右孩子。
具体实现代码:(可运行)
/*
* @Description: 二叉查找树
* @Version: V1.0
* @Autor: Carlos
* @Date: 2020-06-02 15:50:31
* @LastEditors: Carlos
* @LastEditTime: 2020-06-03 16:49:46
*/
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define ElemType int
#define KeyType int
/* 二叉排序树的节点结构定义 */
typedef struct BiTNode
{
int data;
struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;
/**
* @Description: 二叉排序树查找算法
* @Param: BiTree T KeyType key BiTree f BiTree *p
* @Return: 删除成功 TRUE 删除失败 FALSE
* @Author: Carlos
*/
int SearchBST(BiTree T, KeyType key, BiTree f, BiTree *p)
{
//如果 T 指针为空,说明查找失败,令 p 指针指向查找过程中最后一个叶子结点,并返回查找失败的信息
if (!T)
{
*p = f;
return FALSE;
}
//如果相等,令 p 指针指向该关键字,并返回查找成功信息
else if (key == T->data)
{
*p = T;
return TRUE;
}
//如果 key 值比 T 根结点的值小,则查找其左子树;反之,查找其右子树
else if (key < T->data)
{
return SearchBST(T->lchild, key, T, p);
}
else
{
return SearchBST(T->rchild, key, T, p);
}
}
/**
* @Description: 二叉树插入函数
* @Param: BiTree *T 二叉树结构体指针的指针 ElemType e 要插入的元素
* @Return: 删除成功 TRUE 删除失败 FALSE
* @Author: Carlos
*/
int InsertBST(BiTree *T, ElemType e)
{
BiTree p = NULL;
//如果查找不成功,需做插入操作
if (!SearchBST((*T), e, NULL, &p))
{
//初始化插入结点
BiTree s = (BiTree)malloc(sizeof(BiTree));
s->data = e;
s->lchild = s->rchild = NULL;
//如果 p 为NULL,说明该二叉排序树为空树,此时插入的结点为整棵树的根结点
if (!p)
{
*T = s;
}
//如果 p 不为 NULL,则 p 指向的为查找失败的最后一个叶子结点,只需要通过比较 p 和 e 的值确定 s 到底是 p 的左孩子还是右孩子
else if (e < p->data)
{
p->lchild = s;
}
else
{
p->rchild = s;
}
return TRUE;
}
//如果查找成功,不需要做插入操作,插入失败
return FALSE;
}
/**
* @Description: 删除节点的函数
* @Param: BiTree *p 指向结构体指针的指针
* @Return: 删除成功 TRUE
* @Author: Carlos
*/
int Delete(BiTree *p)
{
BiTree q, s;
//情况 1,结点 p 本身为叶子结点,直接删除即可
if (!(*p)->lchild && !(*p)->rchild)
{
*p = NULL;
}
//左子树为空,只需用结点 p 的右子树根结点代替结点 p 即可;
else if (!(*p)->lchild)
{
q = *p;
*p = (*p)->rchild;
free(q);
q = NULL;
}
//右子树为空,只需用结点 p 的左子树根结点代替结点 p 即可;
else if (!(*p)->rchild)
{
q = *p;
//这里不是指针 *p 指向左子树,而是将左子树存储的结点的地址赋值给指针变量 p
*p = (*p)->lchild;
free(q);
q = NULL;
}
//左右子树均不为空,采用第 2 种方式
else
{
q = *p;
s = (*p)->lchild;
//遍历,找到结点 p 的直接前驱
while (s->rchild)
{
//指向p节点左子树最右边节点的前一个。保留下来
q = s;
s = s->rchild;
}
//直接改变结点 p 的值
(*p)->data = s->data;
//判断结点 p 的左子树 s 是否有右子树,分为两种情况讨论 如果有右子树,s一定会指向右子树的叶子节点。q 此时指向的是叶子节点的父节点。 q != *p二者不等说明有右子树
if (q != *p)
{
//若有,则在删除直接前驱结点的同时,令前驱的左孩子结点改为 q 指向结点的孩子结点
q->rchild = s->lchild;
}
else
//q == *p ==NULL 说明没有右子树
{
//否则,直接将左子树上移即可
q->lchild = s->lchild;
}
free(s);
s = NULL;
}
return TRUE;
}
/**
* @Description: 删除二叉树中的元素
* @Param: BiTree *T 指向二叉树结构体的指针 int key 要删除的元素
* @Return: 删除成功 TRUE 删除失败 FALSE
* @Author: Carlos
*/
int DeleteBST(BiTree *T, int key)
{
if (!(*T))
{ //不存在关键字等于key的数据元素
return FALSE;
}
else
{
if (key == (*T)->data)
{
Delete(T);
return TRUE;
}
else if (key < (*T)->data)
{
//使用递归的方式
return DeleteBST(&(*T)->lchild, key);
}
else
{
return DeleteBST(&(*T)->rchild, key);
}
}
}
/**
* @Description: 中序遍历输出二叉树
* @Param: BiTree t 结构体变量
* @Return: 无
* @Author: Carlos
*/
void order(BiTree t)
{
if (t == NULL)
{
return;
}
order(t->lchild);
printf("%d ", t->data);
order(t->rchild);
}
int main()
{
int i;
int a[5] = {3, 4, 2, 5, 9};
BiTree T = NULL;
for (i = 0; i < 5; i++)
{
InsertBST(&T, a[i]);
}
printf("中序遍历二叉排序树:\n");
order(T);
printf("\n");
printf("删除3后,中序遍历二叉排序树:\n");
DeleteBST(&T, 3);
order(T);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
文章来源: blog.csdn.net,作者:嵌入式与Linux那些事,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/qq_16933601/article/details/106500778
- 点赞
- 收藏
- 关注作者




评论(0)