数据结构与算法分析之表、栈和队列（一）

1.前驱元，后继元

对于除空表外的任何表，我们说后继；（或继，之后）并称（i<N）前驱(i>1)。表中的第一个元素是，而最后一个元素是。我们将不定义的前驱元，也不定义的后继元。元素在表中的位置为i。为了简单起见，我们在讨论中将假设表中的元素是整数，但一般说来任意的复元素也是允许的。

ADT  (abstract data type )抽象数据类型

2.链表概念

链表由一系列不必在内存中相连的结构组成。每一个结构均含有表元素和指向包含该元素后继元的结构的指针。我们称之为Next 指针。最后一个单元的Next指针指向NULL；该值由C定义并且不能与其他指针混淆。ANSIC规定NULL为零。

3.链表的访问

指针指向链表的第一个单元。第一个单元包含一个next指针，指向了第二个单元的位置，以此类推。所以访问链表，我们需要知道第一个单元的地址。

4.链表的删除、插入

通过修改指针指向的位置即可删除链表中的元素。

插入命令需要使用一次malloc调用从系统得到一个新单元（后面将详细论述）并在此后执行两次指针调整。其一般想法在图中给出，其中的虚线表示原来的指针。

5.测试链表是否是空表，测试当前位置是否是链表末尾

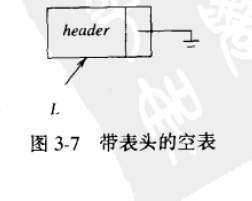
L->next 存放的是指向下一个节点数据域的地址。

L和P不一样吗？(P是指针。L是一个指向链表头节点的指针。（链表每个节点分为数据域和指针域，单链表的指针域只有后继指针域，双链表的指针域分为前趋指针域和后继指针域）)；

6.链表的删除操作

将链表的头结点的next值赋值给P你真。将头结点的指针赋值NULL。使用P指针判断,当P指针不为NULL就将新的链表赋值给一个新的指针。最后返回新链表的地址。 因为之前已经将L->next 赋值为NULL。 所以P指针判断的时候自然会跳过这个节点，遍历整个链表后组成新的链表。（数据结构与算法分析（C语言版）P38）

在网上看到的另一种删除元素的方法。其实就是将要删除的节点与下一个节点的关系变成将要删除节点的下一个元素和下下一个元素的关系。（这么理解可能不怎么恰当）这样P指针就不会指向原来的要删除的元素了。具体看代码（建议画图分析）

实际上就是一步，p->next = p->next->next. 用p来取代p->next;

  

   

    

     

    
    

     

      #include <stdio.h>
     
    
   

    

     

    
    

     

      #define ERROR 0
     
    
   

    

     

    
    

     

      #define OK 1
     
    
   

    

     

    
    

     

      Status ListDelete(LinkList *L,int i ,ElemType *e)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     

      int j;
     
    
   

    

     

    
    

     

      LinkList p,q;
     
    
   

    

     

    
    

     

      p = *L;
     
    
   

    

     

    
    

     

      j = 1;
     
    
   

    

     

    
    

     

      while(p->next && j <i)
     
    
   

    

     

    
    

     

          {
     
    
   

    

     

    
    

     

          p = p->next;
     
    
   

    

     

    
    

     

          ++j;
     
    
   

    

     

    
    

     

          }
     
    
   

    

     

    
    

     

      if(!(p->next) || j>i)
     
    
   

    

     

    
    

     
    return ERROR;
     
    
   

    

     

    
    

     

      q = p->next;
     
    
   

    

     

    
    

     

      p->next = q->next;
     
    
   

    

     

    
    

     

      *e = q->data;
     
    
   

    

     

    
    

     

      free(q);
     
    
   

    

     

    
    

     

      return OK;
     
    
   

    

     

    
    

     

      }
     
    
  
 

最后将q结点中的数据赋值给e，作为返回，并且释放q节点。

7.链表的插入

一个节点分为数据域和指针域。所以插入操作其实就是在要插入的位置生成一块内存空间，存放即将插入的节点。新生成节点s，将其指针域指向要插入位置的数据域部分。将要插入位置的前一个元素的指针域指向s的数据域部分。

  

   

    

     

    
    

     

      /*初始条件：顺序线性表L已存在，1≤i≤ListLength(L)*/
     
    
   

    

     

    
    

     

      /*操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1*/
     
    
   

    

     

    
    

     

      Status ListInsert(LinkList *L,int i ,ElemType e)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     

      int j;
     
    
   

    

     

    
    

     

      LintList p,s; 
     
    
   

    

     

    
    

     

      p = *L;
     
    
   

    

     

    
    

     

      j = 1;
     
    
   

    

     

    
    

     

      while (p && j<i) /*寻找第i个结点*/
     
    
   

    

     

    
    

     

          {
     
    
   

    

     

    
    

     

          p = p->next;
     
    
   

    

     

    
    

     

          ++j;
     
    
   

    

     

    
    

     

          }
     
    
   

    

     

    
    

     

      if (!p || j >i)
     
    
   

    

     

    
    

     
    return ERROR;  /*第i个元素不存在*/
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      s = (LinkList)malloc(sizeof(Node)); /*生成新的结点*/
     
    
   

    

     

    
    

     

      s->data = e;
     
    
   

    

     

    
    

     

      s->next = p->next;  /*将p的后继结点赋值给s的后继*/
     
    
   

    

     

    
    

     

      p->next = s;  /*将s赋值给p的后继*/
     
    
   

    

     

    
    

     

      return OK;
     
    
   

    

     

    
    

     

      }
     
    
  
 

8.malloc

声明指向一个结构的指针并不创建该结构，而只是给出足够的空间容纳结构可能会使用的地址。创建尚未被声明过的记录的惟一方法是使用malloc库函数。malloc（HowManyBytes）使系统创建一个新的结构并返回指向该结构的指针。

当有些空间不再需要时，你可以用free命令通知系统来回收它。free（P）的结果是：P正在指向的地址没变，但在该地址处的数据此时已无定义了。

9.基数排序

原理：准备10个容器，编号0-9，对应数字0-9。 容器是有序的(按添加顺序)
然后按待排序元素的某一位的数字(比如:个位/十位/白位)将其存放到对应容器中（数字相同,如: 个位是数字1时, 就把这个元素放在1号桶），所有元素这样处理完后,
再从0号容器开始依次到9号容器, 将其中的元素顺序取出。所以容器内的元素收集合并复制回原数组，然后再从下一位开始…(比如个位处理完后, 再处理十位/百位....最高位)

这里假设数组元素都是3位数。从个位开始，将数组中的元素按个位数字放入对应的桶中，再从桶中顺序取出到数组，这是数组按个位数字有序排列，再以相同的逻辑处理十位和百位。最后数组中就是有序的了

这里的排序原理是:将元素按位排序, 但是优先级不同,  做高位优先级高, 然后是次高位...。这样考虑：一组元素按最高位排序，那么在不考虑其他位的情况下，这组元素是有序的。再考虑低位，当个位排序好后，在排序十位，这时对十位的排序影响个位了吗？并没有。这就是优先级（权重）的问题， 十位对数字大小的影响显然比个位高。

本文参考《数据结构与算法分析-C语言版》

文章来源: blog.csdn.net，作者：嵌入式与Linux那些事，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/qq_16933601/article/details/100072295