1 引例

给定如图所示的某个函数，如何通过计算机算法编程求 $f(x)_{min}$？

2 数值解法

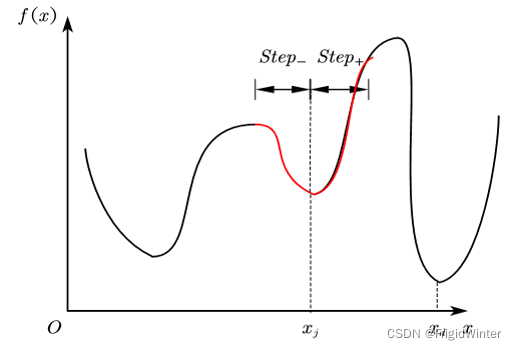
传统方法是数值解法，如图所示

按照以下步骤迭代循环直至最优：

① 任意给定一个初值 $x_0$；

② 随机生成增量方向，结合步长生成 $\varDelta x$；

③ 计算比较 $f\left( x_0 \right)$与 $f\left( x_0+\varDelta x \right)$的大小，若 $f\left( x_0+\varDelta x \right) <f\left( x_0 \right)$则更新位置，否则重新生成 $\varDelta x$；

④ 重复②③直至收敛到最优 $f(x)_{min}$。

数值解法最大的优点是编程简明，但缺陷也很明显：

① 初值的设定对结果收敛快慢影响很大；

② 增量方向随机生成，效率较低；

③ 容易陷入局部最优解；

④ 无法处理“高原”类型函数。

所谓陷入局部最优解是指当迭代进入到某个极小值或其邻域时，由于步长选择不恰当，无论正方向还是负方向，学习效果都不如当前，导致无法向全局最优迭代。就本问题而言如图所示，当迭代陷入 $x=x_j$时，由于学习步长 $step$的限制，无法使 $f\left( x_j\pm Step \right) <f(x_j)$，因此迭代就被锁死在了图中的红色区段。可以看出 $x=x_j$并非期望的全局最优。

若出现下图所示的“高原”函数，也可能使迭代得不到更新。

3 梯度下降算法

梯度下降算法可视为数值解法的一种改进，阐述如下：

记第 $k$轮迭代后，自变量更新为 $x=x_k$，令目标函数 $f(x)$在 $x=x_k$泰勒展开：

$$f\left( x \right) =f\left( x_k \right) +f'\left( x_k \right) \left( x-x_k \right) +o(x)$$

考察 $f(x)_{min}$，则期望 $f\left( x_{k+1} \right) <f\left( x_k \right)$，从而：

$$f\left( x_{k+1} \right) -f\left( x_k \right) =f'\left( x_k \right) \left( x_{k+1}-x_k \right) <0$$

若 $f'\left( x_k \right) >0$则 $x_{k+1}<x_k$，即迭代方向为负；反之为正。不妨设 $x_{k+1}-x_k=-f'(x_k)$，从而保证 $f\left( x_{k+1} \right) -f\left( x_k \right) <0$。必须指出，泰勒公式成立的条件是 $x\rightarrow x_0$，故 $|f'\left( x_k \right) |$不能太大，否则 $x_{k+1}$与 $x_{k}$距离太远产生余项误差。因此引入学习率 $\gamma \in \left( 0, 1 \right)$来减小偏移度，即 $x_{k+1}-x_k=-\gamma f'(x_k)$

在工程上，学习率 $\gamma$要结合实际应用合理选择，== $\gamma$过大会使迭代在极小值两侧振荡，算法无法收敛； $\gamma$过小会使学习效率下降，算法收敛慢==。

对于向量 ，将上述迭代公式推广为

$${\boldsymbol{x}_{\boldsymbol{k}+1}=\boldsymbol{x}_{\boldsymbol{k}}-\gamma \nabla _{\boldsymbol{x}_{\boldsymbol{k}}}}$$

其中 $\nabla _{\boldsymbol{x}}=\left( \frac{\partial f(\boldsymbol{x})}{\partial x_1},\frac{\partial f(\boldsymbol{x})}{\partial x_2},\cdots \cdots ,\frac{\partial f(\boldsymbol{x})}{\partial x_n} \right) ^T$为多元函数的梯度，故此迭代算法也称为梯度下降算法

梯度下降算法通过函数梯度确定了每一次迭代的方向和步长，提高了算法效率。但从原理上可以知道，此算法并不能解决数值解法中初值设定、局部最优陷落和部分函数锁死的问题。

4 代码实战：Logistic回归

import pandas as pd
import numpy as np
import os
import matplotlib.pyplot as plt
import matplotlib as mpl
from Logit import Logit

'''
* @breif: 从CSV中加载指定数据
* @param[in]: file -> 文件名
* @param[in]: colName -> 要加载的列名
* @param[in]: mode -> 加载模式, set: 列名与该列数据组成的字典, df: df类型
* @retval: mode模式下的返回值
'''
def loadCsvData(file, colName, mode='df'):
    assert mode in ('set', 'df')
    df = pd.read_csv(file, encoding='utf-8-sig', usecols=colName)
    if mode == 'df':
        return df
    if mode == 'set':
        res = {}
        for col in colName:
            res[col] = df[col].values
        return res

if __name__ == '__main__':
    # ============================
    # 读取CSV数据
    # ============================
    csvPath = os.path.abspath(os.path.join(__file__, "../../data/dataset3.0alpha.csv"))
    dataX = loadCsvData(csvPath, ["含糖率", "密度"], 'df')
    dataY = loadCsvData(csvPath, ["好瓜"], 'df')
    label = np.array([
        1 if i == "是" else 0
        for i in list(map(lambda s: s.strip(), list(dataY['好瓜'])))
    ])

    # ============================
    # 绘制样本点
    # ============================
    line_x = np.array([np.min(dataX['密度']), np.max(dataX['密度'])])
    mpl.rcParams['font.sans-serif'] = [u'SimHei']
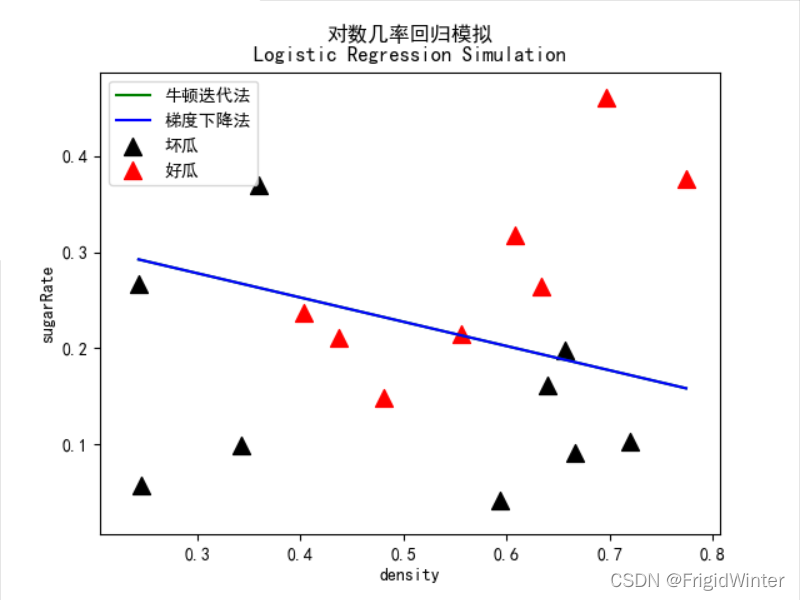
    plt.title('对数几率回归模拟\nLogistic Regression Simulation')
    plt.xlabel('density')
    plt.ylabel('sugarRate')
    plt.scatter(dataX['密度'][label==0],
                dataX['含糖率'][label==0],
                marker='^',
                color='k',
                s=100,
                label='坏瓜')
    plt.scatter(dataX['密度'][label==1],
                dataX['含糖率'][label==1],
                marker='^',
                color='r',
                s=100,
                label='好瓜')

    # ============================
    # 实例化对数几率回归模型
    # ============================
    logit = Logit(dataX, label)

    # 采用梯度下降法
    logit.logitRegression(logit.gradientDescent)
    line_y = -logit.w[0, 0] / logit.w[1, 0] * line_x - logit.w[2, 0] / logit.w[1, 0]
    plt.plot(line_x, line_y, 'b-', label="梯度下降法")

    # 绘图
    plt.legend(loc='upper left')
    plt.show()

🔥 更多精彩专栏：

• 《机器人原理与技术》
• 《计算机视觉教程》
• 《机器学习》
• 《嵌入式系统》
• 《数值优化方法》
• …

🏠 欢迎加入社区和更多志同道合的朋友交流：AI 技术社