1 仿生分析

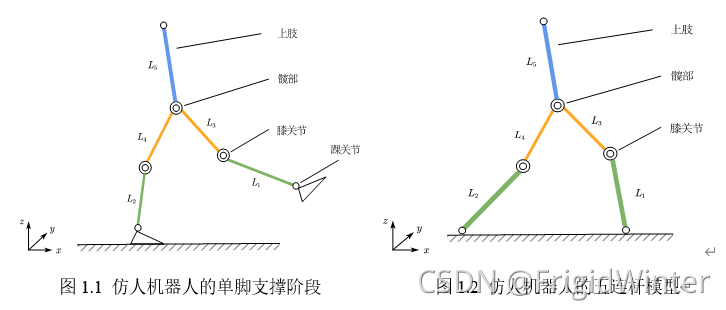
仿人机器人是基于仿生原理，在机械结构和运动过程上模仿人的行为以达到预期性能的机电装置。如图1.1所示，一般地，仿人机器人结构可分为七连杆，主导运动的腿部主要由髋关节、膝关节、踝关节组成，其余为上肢。

与人类似，在机器人行走运动过程中分为三个阶段：单脚支撑、落地碰撞与双脚支撑阶段。机器人处于单脚支撑阶段时，摆动腿膝关节被动摆动，但在落地碰撞进入双脚支撑阶段之前，摆动腿会绷直以更好地支撑身体重量 $^{[1]}$。有研究指出 $^{[2]}$，髋关节、膝关节在机器人行走、跑步等常规运动——即单脚支撑与双脚支撑阶段占有主导地位；而踝关节的分析在这两个阶段中并不必要，其作用体现在落地碰撞瞬间的驱动力上。

因此，仿人机器人运动系统模型可以分为两个方面：

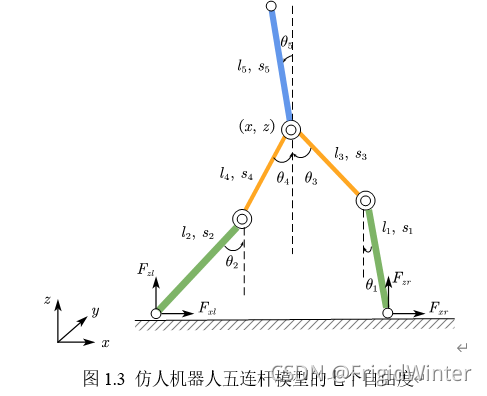
1. 单脚支撑与双脚支撑阶段，此时不考虑踝关节驱动，机器人简化为五连杆模型，如图1.2所示；
2. 落地碰撞阶段，此时踝关节提供驱动并产生自由度变化。
   仿人机器人的综合模型可视为上述两个方面的叠加 $^{[3]}$。

2 模型假设

2.1 单脚支撑与双脚支撑阶段

此时机器人为五连杆模型，转动关节本身产生五个转动自由度 $\theta _i\left( i=1,2,3,4,5 \right)$，分别由五个驱动力矩 $\tau _i\left( i=1,2,3,4,5 \right)$作用。假设基坐标系位于髋部，当髋关节位置不变时，机器人的位姿完全由上述五个自由度表征。但当机器人运动产生髋部位移时，基坐标系随之移动，此时需要额外增加两个自由度来描述这种变化，这里把这两个自由度体现在髋部坐标上。综上所述，仿人机器人在单脚支撑和双脚支撑阶段共7个自由度构成关节向量：

$$\boldsymbol{\theta }=\left[ \begin{matrix} \theta _1& \theta _2& \theta _3& \theta _4& \theta _5& x& z\\\end{matrix} \right] ^T$$

5个驱动力矩构成控制输入：

$$\boldsymbol{\tau }=\left[ \begin{matrix} \tau _1& \tau _2& \tau _3& \tau _4& \tau _5\\\end{matrix} \right] ^T$$

2.2 落地碰撞阶段

建立仿人机器人多体动力学模型最重要的一点就是怎样处理脚和地面的接触面。一般地，认为机器人是多刚体系统，且一般地面刚度很大，因此机器人足端与地面为刚性接触。落地碰撞瞬时发生，且为完全非弹性碰撞，从而碰撞前后，机器人仅发生速度突变而没有位置的突变，且碰撞后摆动腿不发生弹起和滑移。有研究采用弹簧防震器和误差项来控制地面和系统的反作用 $^{[4]}$；有研究采用Hertz模型来表示地面接触力 $^{[5]}$。这里采用Hertz模型：

$$\begin{cases} \boldsymbol{F}_l=\left[ \begin{array}{c} F_{xl}\\ F_{zl}\\\end{array} \right] =\left[ \begin{array}{c} F_{xl}\\ K\left| z_l \right|^n+\lambda \dot{z}_l\left| z_l \right|^n\\\end{array} \right]\\ \boldsymbol{F}_r=\left[ \begin{array}{c} F_{xr}\\ F_{zr}\\\end{array} \right] =\left[ \begin{array}{c} F_{xr}\\ K\left| z_r \right|^n+\lambda \dot{z}_r\left| z_r \right|^n\\\end{array} \right]\\\end{cases}$$

其中 $K$为地面刚度系数， $\lambda$为阻尼系数， $n$为赫兹系数， $(x_l, z_l)$、 $(x_r, z_r)$分别为左、右足的空间坐标，对于关节向量 ，将碰撞时的约束力映射为约束力矩向量(对移动自由度而言为力)：

$$\begin{cases} \boldsymbol{\tau }_l=\boldsymbol{C}_l\boldsymbol{F}_l\\ \boldsymbol{\tau }_r=\boldsymbol{C}_r\boldsymbol{F}_r\\\end{cases}$$

3 模型建立

采用拉格朗日方程建立动力学模型，列出各连杆重心坐标如下：

$$\begin{cases} \bar{x}_1=x+l_3\sin \theta _3+s_1\sin \theta _1\\ \bar{x}_2=x-l_4\sin \theta _4-s_2\sin \theta _2\\ \bar{x}_3=x+s_3\sin \theta _3\\ \bar{x}_4=x-s_4\sin \theta _4\\ \bar{x}_5=x-s_5\sin \theta _5\\\end{cases}\,\, \begin{cases} \bar{z}_1=z-l_3\cos \theta _3-s_1\cos \theta _1\\ \bar{z}_2=z-l_4\cos \theta _4-s_2\cos \theta _2\\ \bar{z}_3=z-s_3\cos \theta _3\\ \bar{z}_4=z-s_4\cos \theta _4\\ \bar{z}_5=z+s_5\cos \theta _5\\\end{cases}$$

其中 $s_i\left( i=1,2,3,4,5 \right)$为连杆重心位置。

设髋部为零势能点，则系统总势能为：

$$U=\sum_{i=1}^5{m_ig\bar{z}_i}\\=-m_1g\left( l_3\cos \theta _3+s_1\cos \theta _1 \right) -m_2g\left( l_4\cos \theta _4+s_2\cos \theta _2 \right) -m_3gs_3\cos \theta _3-m_4gs_4\cos \theta _4+m_5gs_5\cos \theta _5$$

将系统连杆动能分解为平动动能和转动动能,根据 $K_i=\frac{1}{2}m_i\left( \dot{\bar{x}}_{i}^{2}+\dot{\bar{z}}_{i}^{2} \right) +\frac{1}{2}J_i\dot{\theta}_{i}^{2}$，其中 $J_i$为第 $i$根连杆的转动惯量，可得：

$$\begin{cases} K_1=\frac{1}{2}m_1\left[ \dot{x}^2+\dot{z}^2+2l_3\dot{\theta}_3\dot{x}\cos \theta _3+2s_1\dot{\theta}_1\dot{x}\cos \theta _1+2l_3\dot{\theta}_3\dot{z}\sin \theta _3+2s_1\dot{\theta}_1\dot{z}\sin \theta _1+2l_3s_1\dot{\theta}_1\dot{\theta}_3\cos \left( \theta _1-\theta _3 \right) +l_{3}^{2}\dot{\theta}_{3}^{2}+s_{1}^{2}\dot{\theta}_{1}^{2} \right] +\frac{1}{2}J_1\dot{\theta}_{1}^{2}\\ K_2=\frac{1}{2}m_2\left[ \dot{x}^2+\dot{z}^2-2l_4\dot{\theta}_4\dot{x}\cos \theta _4-2s_2\dot{\theta}_2\dot{x}\cos \theta _2+2l_4\dot{\theta}_4\dot{z}\sin \theta _4+2s_2\dot{\theta}_2\dot{z}\sin \theta _2+2l_4s_2\dot{\theta}_2\dot{\theta}_4\cos \left( \theta _2-\theta _4 \right) +l_{4}^{2}\dot{\theta}_{4}^{2}+s_{2}^{2}\dot{\theta}_{2}^{2} \right] +\frac{1}{2}J_2\dot{\theta}_{2}^{2}\\ K_3=\frac{1}{2}m_3\left[ \dot{x}^2+\dot{z}^2+2s_3\dot{\theta}_3\dot{x}\cos \theta _3+2s_3\dot{\theta}_3\dot{z}\sin \theta _3+s_{3}^{2}\dot{\theta}_{3}^{2} \right] +\frac{1}{2}J_3\dot{\theta}_{3}^{2}\\ K_4=\frac{1}{2}m_4\left[ \dot{x}^2+\dot{z}^2-2s_4\dot{\theta}_4\dot{x}\cos \theta _4+2s_4\dot{\theta}_4\dot{z}\sin \theta _4+s_{4}^{2}\dot{\theta}_{4}^{2} \right] +\frac{1}{2}J_4\dot{\theta}_{4}^{2}\\ K_5=\frac{1}{2}m_5\left[ \dot{x}^2+\dot{z}^2-2s_5\dot{\theta}_5\dot{x}\cos \theta _5-2s_5\dot{\theta}_5\dot{z}\sin \theta _5+s_{5}^{2}\dot{\theta}_{5}^{2} \right] +\frac{1}{2}J_5\dot{\theta}_{5}^{2}\\\end{cases}$$

由拉格朗日函数 $L=K-U$知

$$\begin{cases} \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial \dot{\theta}_1} \right) -\frac{\partial L}{\partial \theta _1}=\left( m_1s_{1}^{2}+J_1 \right) \ddot{\theta}_1+m_1l_3s_1\ddot{\theta}_3\cos \left( \theta _1-\theta _3 \right) +m_1s_1\ddot{x}\cos \theta _1+m_1s_1\ddot{z}\sin \theta _1+m_1l_3s_1\dot{\theta}_{3}^{2}\sin \left( \theta _1-\theta _3 \right)\\ \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial \dot{\theta}_2} \right) -\frac{\partial L}{\partial \theta _2}=\left( m_2s_{2}^{2}+J_2 \right) \ddot{\theta}_2+m_2l_4s_2\ddot{\theta}_4\cos \left( \theta _2-\theta _4 \right) -m_2s_2\ddot{x}\cos \theta _2+m_2s_2\ddot{z}\sin \theta _2+m_2l_4s_2\dot{\theta}_{4}^{2}\sin \left( \theta _2-\theta _4 \right)\\ \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial \dot{\theta}_3} \right) -\frac{\partial L}{\partial \theta _3}=\left( m_1l_{3}^{2}+m_3s_{3}^{2}+J_3 \right) \ddot{\theta}_3+m_1l_3s_1\ddot{\theta}_1\cos \left( \theta _1-\theta _3 \right) +\left( m_1l_3+m_3s_3 \right) \ddot{x}\cos \theta _3+\left( m_1l_3+m_3s_3 \right) \ddot{z}\sin \theta _3-m_1l_3s_1\dot{\theta}_{1}^{2}\sin \left( \theta _1-\theta _3 \right)\\ \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial \dot{\theta}_4} \right) -\frac{\partial L}{\partial \theta _4}=\left( m_2l_{4}^{2}+m_4s_{4}^{2}+J_4 \right) \ddot{\theta}_4+m_2l_4s_2\ddot{\theta}_2\cos \left( \theta _2-\theta _4 \right) -\left( m_2l_4+m_4s_4 \right) \ddot{x}\cos \theta _4+\left( m_2l_4+m_4s_4 \right) \ddot{z}\sin \theta _4-m_2l_4s_2\dot{\theta}_{2}^{2}\sin \left( \theta _2-\theta _4 \right)\\ \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial \dot{\theta}_5} \right) -\frac{\partial L}{\partial \theta _5}=\left( m_5s_{5}^{2}+J_5 \right) \ddot{\theta}_5-m_5s_5\ddot{x}\cos \theta _5-m_5s_5\ddot{z}\sin \theta _5\\ \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial \dot{x}} \right) -\frac{\partial L}{\partial x}=\left( m_1+m_2+m_3+m_4+m_5 \right) \ddot{x}+m_1s_1\ddot{\theta}_1\cos \theta _1-m_2s_2\ddot{\theta}_2\cos \theta _2+\left( m_1l_3+m_3s_3 \right) \ddot{\theta}_3\cos \theta _3-\left( m_2l_4+m_4s_4 \right) \ddot{\theta}_4\cos \theta _4\\ \,\, -m_5s_5\ddot{\theta}_5\cos \theta _5-m_1s_1\dot{\theta}_{1}^{2}\sin \theta _1+m_2s_2\dot{\theta}_{2}^{2}\sin \theta _2-\left( m_1l_3+m_3s_3 \right) \dot{\theta}_{3}^{2}\sin \theta _3+\left( m_2l_4+m_4s_4 \right) \dot{\theta}_{4}^{2}\sin \theta _4+m_5s_5\dot{\theta}_{5}^{2}\sin \theta _5\\ \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial \dot{z}} \right) -\frac{\partial L}{\partial z}=\left( m_1+m_2+m_3+m_4+m_5 \right) \ddot{z}+m_1s_1\ddot{\theta}_1\sin \theta _1+m_2s_2\ddot{\theta}_2\sin \theta _2+\left( m_1l_3+m_3s_3 \right) \ddot{\theta}_3\sin \theta _3+\left( m_2l_4+m_4s_4 \right) \ddot{\theta}_4\sin \theta _4\\ \,\, -m_5s_5\ddot{\theta}_5\sin \theta _5+m_1s_1\dot{\theta}_{1}^{2}\cos \theta _1+m_2s_2\dot{\theta}_{2}^{2}\cos \theta _2+\left( m_1l_3+m_3s_3 \right) \dot{\theta}_{3}^{2}\cos \theta _3+\left( m_2l_4+m_4s_4 \right) \dot{\theta}_{4}^{2}\cos \theta _4-m_5s_5\dot{\theta}_{5}^{2}\sin \theta _5\\\end{cases}$$

由拉格朗日方程 $\boldsymbol{\tau }=\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial \boldsymbol{\dot{\theta}}} \right) -\frac{\partial L}{\partial \boldsymbol{\theta }}$结合第二节的理论，关节向量 可视为单脚支撑、双脚支撑阶段与落地碰撞阶段的叠加：

$$\boldsymbol{B\tau }+\boldsymbol{\tau }_l+\boldsymbol{\tau }_r=\boldsymbol{D}_1\left( \boldsymbol{\theta } \right) \boldsymbol{\ddot{\theta}}+\boldsymbol{D}_2\left( \boldsymbol{\theta } \right) \boldsymbol{\dot{\theta}}^2+\boldsymbol{D}_4\left( \boldsymbol{\theta } \right)$$

其中

$$\boldsymbol{D}_1\left( \boldsymbol{\theta } \right) =\left[ \begin{matrix} m_1s_{1}^{2}+J_1& 0& m_1l_3s_1\cos \left( \theta _1-\theta _3 \right)& 0& 0& m_1s_1\cos \theta _1& m_1s_1\sin \theta _1\\ & m_2s_{2}^{2}+J_2& 0& m_2l_4s_2\cos \left( \theta _2-\theta _4 \right)& 0& -m_2s_2\cos \theta _2& m_2s_2\sin \theta _2\\ \vdots& & m_1l_{3}^{2}+m_3s_{3}^{2}+J_3& 0& 0& \left( m_1l_3+m_3s_3 \right) \cos \theta _3& \left( m_1l_3+m_3s_3 \right) \sin \theta _3\\ & & & m_2l_{4}^{2}+m_4s_{4}^{2}+J_4& 0& -\left( m_2l_4+m_4s_4 \right) \cos \theta _4& \left( m_2l_4+m_4s_4 \right) \sin \theta _4\\ \vdots& & \ddots& & m_5s_{5}^{2}+J_5& -m_5s_5\cos \theta _5& -m_5s_5\sin \theta _5\\ & \ddots& & & & m_1+m_2+m_3+m_4+m_5& 0\\ & & \cdots& & \cdots& & m_1+m_2+m_3+m_4+m_5\\\end{matrix} \right]$$

$$\boldsymbol{D}_2\left( \boldsymbol{\theta } \right) =\left[ \begin{matrix} 0& 0& m_1l_3s_1\sin \left( \theta _1-\theta _3 \right)& 0& 0& 0& 0\\ 0& 0& 0& m_2l_4s_2\sin \left( \theta _2-\theta _4 \right)& 0& 0& 0\\ -m_1l_3s_1\sin \left( \theta _1-\theta _3 \right)& 0& 0& 0& 0& 0& 0\\ 0& -m_2l_4s_2\sin \left( \theta _2-\theta _4 \right)& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ -m_1s_1\sin \theta _1& m_2s_2\sin \theta _2& -\left( m_1l_3+m_3s_3 \right) \sin \theta _3& \left( m_2l_4+m_4s_4 \right) \sin \theta _4& m_5s_5\sin \theta _5& 0& 0\\ m_1s_1\cos \theta _1& m_2s_2\cos \theta _2& \left( m_1l_3+m_3s_3 \right) \cos \theta _3& \left( m_2l_4+m_4s_4 \right) \cos \theta _4& -m_5s_5\sin \theta _5& 0& 0\\\end{matrix} \right]$$

$$\boldsymbol{D}_4\left( \boldsymbol{\theta } \right) =\left[ \begin{array}{c} -m_1gs_1\sin \theta _1\\ -m_2gs_2\sin \theta _2\\ -m_3gs_3\sin \theta _3-m_1gl_3\sin \theta _3\\ -m_4gs_4\sin \theta _4-m_2gl_4\sin \theta _4\\ m_5gs_5\sin \theta _5\\ 0\\ 0\\\end{array} \right]$$

$\boldsymbol{\tau }_l\text{、}\boldsymbol{\tau }_r$为碰撞接触约束力矩， $B$为转矩连接矩阵

4 参考文献

[1]王健美, 付成龙, 黄元林,等. 基于Matlab的双足机器人动力学仿真及仿生控制平台[J]. 系统仿真学报, 2011(05):977-983.
[2] Chevallereau C , Abba G , Aoustin Y , et al. RABBIT: A Testbed for Advanced Control Theory[J]. Control Systems IEEE, 2013, 23(5):57-79.
[3]槐创锋, 刘平安. 七连杆双足机器人建模和控制系统仿真[J]. 计算机仿真, 2010.
[4]槐创锋, 方跃法. 5连杆双足机器人建模和控制系统仿真[J]. 系统仿真学报, 2008, 27(020):5682-5686.

🔥 更多精彩专栏：

• 《机器人原理与技术》
• 《计算机视觉教程》
• 《机器学习》
• 《嵌入式系统》
• 《数值优化方法》
• …

🏠 欢迎加入社区和更多志同道合的朋友交流：AI 技术社