从而可以从成像面坐标还原三维坐标，并转换为像素尺度:

$$\left[ \begin{array}{c} X\\ Y\\ Z\\\end{array} \right] =\left[ \begin{array}{c} ^L\!\!\:x\frac{b_x}{d}\\ ^L\!\!\:y\frac{b_x}{d}\\ f\frac{b_x}{d}\\\end{array} \right] =\left[ \begin{array}{c} \left( ^L\!\!\:u-^L\!\!\:c_u \right) \frac{b_x}{d_u}\\ \left( ^L\!\!\:v-^L\!\!\:c_v \right) \frac{b_x}{d_u}\\ f_u\frac{b_x}{d_u}\\\end{array} \right]$$

其中 $Z$即为==图像深度信息==。将上述方程改写为线性形式:

$$\left[ \begin{array}{c} X\\ Y\\ Z\\ 1\\\end{array} \right] =\left[ \begin{matrix} 1& 0& 0& -^L\!\!\:c_u\\ 0& 1& 0& -^L\!\!\:c_v\\ 0& 0& 0& f_u\\ 0& 0& \frac{1}{b_x}& \frac{^R\!\!\:c_u-^L\!\!\:c_u}{b_x}\\\end{matrix} \right] \left[ \begin{array}{c} ^L\!\!\:u\\ ^L\!\!\:v\\ d_u\\ 1\\\end{array} \right] \Leftrightarrow { ^L\!\boldsymbol{X}=\boldsymbol{Q}^L\!\!\:\boldsymbol{u}}$$

其中 $Q$称为重投影矩阵， $\frac{^R\!\!\:c_u-^L\!\!\:c_u}{b_x}$表征了两成像平面中心的像素偏差。

2 立体校正

实际应用时并不能直接使用上面的模型，因为没有任何硬件可以真正达到理想双目系统的条件，如图2所示。

将实际双目系统变换为理想双目系统的过程称为==立体校正==，下面详细阐述==Bouguet立体校正算法==，其核心原理是通过像素平面透视变换，使左右图像重投影误差最小，使双目系统最接近理想状态。

定义左右两相机间的变换关系为

$$_{\boldsymbol{L}}^{\boldsymbol{R}}\boldsymbol{T}=\left[ \begin{matrix} \boldsymbol{R}& \boldsymbol{t}\\ 0& 1\\\end{matrix} \right]$$

通过旋转矩阵 $R$先将右相机坐标系旋转到与左相机坐标系平行，如图3所示。

此时双目系统平行但不共面，需要构造一个校准矩阵 $R_{rect}$将两相机坐标系旋转到同一成像面上，实现共面行对齐校正，如图4所示。

设 $\boldsymbol{R}_{rect}=\left[ \begin{matrix} \boldsymbol{r}_{1}^{T}& \boldsymbol{r}_{2}^{T}& \boldsymbol{r}_{3}^{T}\\\end{matrix} \right] ^T$，其构造过程如下：

① $r_1$是旋转后坐标系的 $x'$相对于原坐标系三个轴的方向余弦，为保证旋转后两成像面共面，需要将原坐标系 $x$轴旋转至基线 $-t$方向，即

$$\boldsymbol{r}_1=\frac{-\boldsymbol{t}}{\left\| \boldsymbol{t} \right\|}$$

② $r_2$、 $r_3$事实上可以任意给出，只需满足右手系方向即可。一般地，取

$$\begin{cases} \boldsymbol{r}_2=\frac{-\boldsymbol{t}\times \left[ \begin{matrix} 0& 0& 1\\\end{matrix} \right] ^T}{\left\| -\boldsymbol{t}\times \left[ \begin{matrix} 0& 0& 1\\\end{matrix} \right] ^T \right\|}\\ \boldsymbol{r}_3=\boldsymbol{r}_1\times \boldsymbol{r}_2\\\end{cases}$$

使 $y'$垂直于原光轴方向。

综合上述步骤得到

$$\begin{cases} \boldsymbol{R}_L=\boldsymbol{R}_{rect}\\ \boldsymbol{R}_R=\boldsymbol{R}_{rect}\boldsymbol{R}^T\\\end{cases}$$

接下来进行像素平面的映射。在不考虑畸变的条件下，相机坐标系未旋转时有 $\boldsymbol{u}=\boldsymbol{Kx}$，旋转后则为 $\boldsymbol{u}'=\boldsymbol{Kx}'=\boldsymbol{KRx}$，因此旋转前后像素坐标的关系为

$${ \boldsymbol{u}'=\boldsymbol{KRK}^{-1}\boldsymbol{u}=\boldsymbol{Hu}}$$

像素立体校正后，即可使用理想双目系统模型进行场景几何的估计。

总结Bouguet立体校正算法流程：

(1) 基于相机几何信息 $R$、 $t$ 构造 $R_L$、 $R_R$；
(2) 基于旋转前后像素坐标关系得到单应性矩阵 $\boldsymbol{H}_L=\boldsymbol{KR}_L\boldsymbol{K}^{-1}$、 $\boldsymbol{H}_R=\boldsymbol{KR}_R\boldsymbol{K}^{-1}$；
(3) 归一化齐次坐标。映射后 $\boldsymbol{u}'=\left[ \begin{matrix} u& v& w\\\end{matrix} \right]$，需归一化为 $\boldsymbol{u}'=\left[ \begin{matrix} u/w& v/w& 1\\\end{matrix} \right]$。

关于单应性矩阵方面的知识可以参考计算机视觉系列教程1-2：单应性矩阵估计

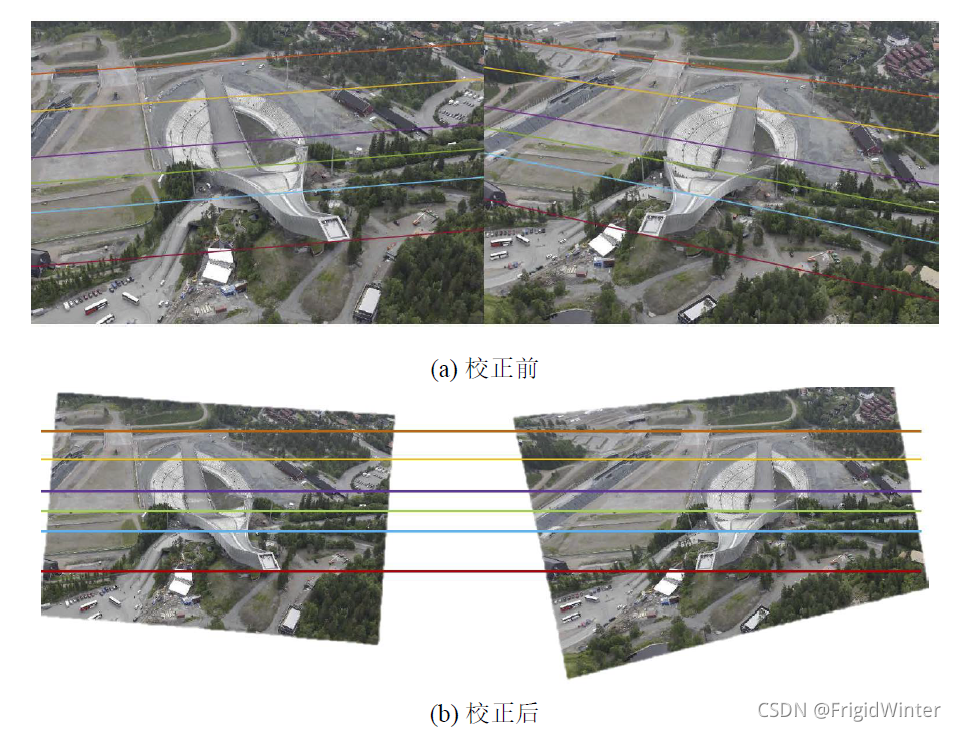
3 实例

🚀 计算机视觉基础教程说明

章号                                    内容
  0               色彩空间与数字成像
  1               计算机几何基础
  2               图像增强、滤波、金字塔
  3               图像特征提取
  4               图像特征描述
  5               图像特征匹配
  6               立体视觉
  7               项目实战

🔥 更多精彩专栏：

• 《机器人原理与技术》
• 《计算机视觉教程》
• 《机器学习》
• 《嵌入式系统》
• 《数值优化方法》
• …
  
  

👇配套代码 · 优质体验 · 系统知识 请关注👇