
1 导论
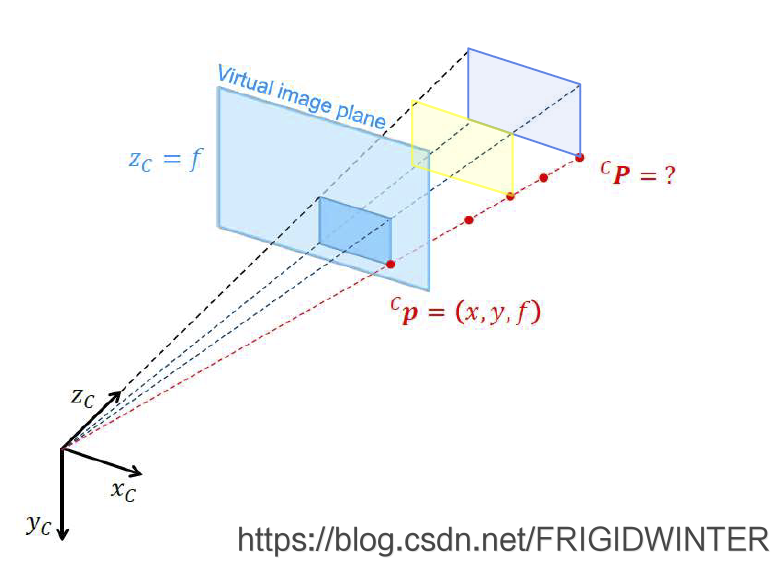
透视几何的缺陷是图像深度信息的丢失,如图1所示,根据相似变换关系,视线上的若干平面都映射为成像面上的一个平面。

图1
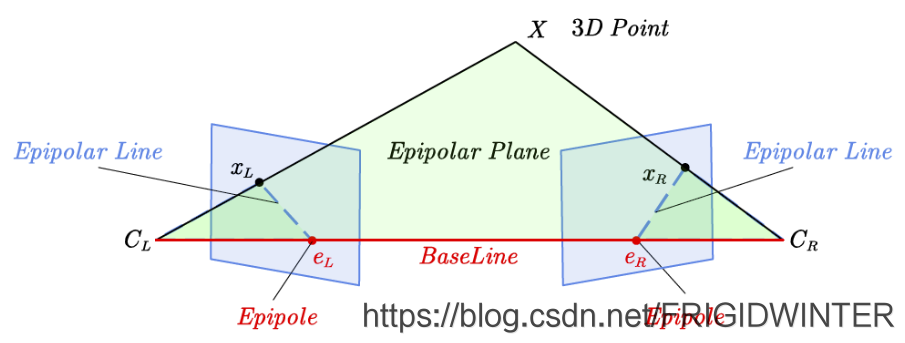
对极几何是两个透视几何模型间的几何约束关系,主要用于实现基于三角测量的双目立体视觉、深度估计等,对极几何约束只能实现点到线的映射,因此约束条件弱于透视几何。图2展示了对极几何的基本概念,其中3D世界的真实点称为物点
X;物点在相机成像面上形成像点
xL、
xR;两台透视相机间光心的连线称为基线;基线与成像面的交点称为极点
eL、
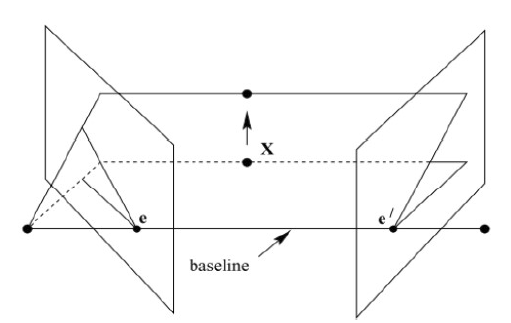
eR,若图像中不存在极点,则说明两个摄像机不能拍摄到彼此;像点与极点的连线称为极线,所有极线相交于极点;透视相机光心与物点确定的平面称为极平面,对于不同物点,极平面绕基线旋转,极线绕极点矩形,如图3所示。

图2

图3(图源网络)
2 对极约束推导
下面讨论两个透视模型间的关系。不妨以左侧相机为参考,设物点
LX=[XYZ]T,左右两相机间的变换关系为
LRT=[R0t1]
则物点在右透视相机坐标系里的3D坐标为
RX=LRTLX=R⎣⎢⎡XYZ⎦⎥⎤+t=⎣⎢⎡X′Y′Z′⎦⎥⎤
事实上,向量
t与成像面的交点即为极点。
根据相似关系,物点在左、右成像面上几何坐标为
⎩⎪⎪⎨⎪⎪⎧xL=fLZXyL=fLZYzL=fL⇒Lx=ZfLLX⎩⎪⎪⎨⎪⎪⎧xR=fRZ′X′yR=fRZ′Y′zR=fR⇒Rx=Z′fRRX
结合齐次变换关系,有
Rx=Z′fR(RLX+t)=Z′fR(RfLZ⋅Lx+t)=αRLx+βt
其中
α、
β为两个与尺度有关的常数。将等式两边同时与向量
t做外积,有
Rx×t=(αRLx+βt)×t
线性化为
t∧Rx=αt∧RLx
两边同乘
RxT,考虑到
RxT与向量
Rx×t垂直,故
αRxTt∧RLx=0
消去常数
α,即得
RxTELx=0
其中
E=t∧R称为本征矩阵(Essential Matrix),表征了同一物点在两个透视相机成像面上像点的几何约束关系。
下面引入相机内参矩阵,将像点映射到像素平面
{Lu=KLLxRu=KRRx
代入上式即得
RuTFLu=0
其中
F=KR−TEKL−1称为基本矩阵(Fundamental Matrix),表征了同一物点在两个透视相机像素面上像素点间的几何约束关系。
本征矩阵与基本矩阵表征了两个透视模型对极几何的代数特征,以上二式共同构成对极约束(Epipolar Constraint)。
🚀 计算机视觉基础教程说明
章号 内容
0 色彩空间与数字成像
1 计算机几何基础
2 图像增强、滤波、金字塔
3 图像特征提取
4 图像特征描述
5 图像特征匹配
6 立体视觉
7 项目实战
🔥 更多精彩专栏:
👇配套代码 · 优质体验 · 系统知识 请关注👇

【版权声明】本文为华为云社区用户原创内容,未经允许不得转载,如需转载请自行联系原作者进行授权。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com




评论(0)