【数据结构和算法】图论，这个算法你学会了吗？
🎈 作者：Linux猿
🎈 简介：CSDN博客专家🏆，华为云享专家🏆，Linux、C/C++、云计算、物联网、面试、刷题、算法尽管咨询我，关注我，有问题私聊！
🎈 关注专栏： 数据结构和算法成神路【精讲】优质好文持续更新中……🚀🚀🚀
🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬
目录
最小生成树算法有两种「普里姆（Prim）」算法和「克鲁斯卡尔（Kruskal）」算法，其中，「普里姆（Prim）」算法适合于稠密图，「克鲁斯卡尔（Kruskal）」算法适合于稀疏图，本篇文章先对「普里姆（Prim）」算法进行介绍。
🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶
一、什么是最小生成树 ？
在介绍具体算法之前，先来说下什么是「最小生成树」？
假设在 n 个城市之间铺设网络，使得 n 个城市能够互相通信，已知任意两个城市之间铺设网络的费用，如何使得费用最小？
很显然，只需要铺设 n - 1 条线路即可使得 n 个城市能够互相通信。（n 个点构成一个连通图至少需要 n - 1 条边）。
「最小生成树」是指构造连通网的最小代价生成树，所以最小生成树具有 n 个顶点 n - 1 条边。
构造一个连通网的最小生成树有两大算法：「普里姆（Prim）」算法和「克鲁斯卡尔（Kruskal）」算法。
本篇文章先来介绍一下 「普里姆（Prim）」 算法，「克鲁斯卡尔（Kruskal）」算法会在下一篇文章讲解。
🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶
二、普里姆算法（Prim）
2.0 算法起源
「普里姆（Prim）」 在 1930 年由捷克数学家【沃伊捷赫·亚尔尼克】发现；并在 1957 年由美国计算机科学家【罗伯特·普里姆】独立发现；1959 年，【艾兹格·迪科斯彻】再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。
2.1 算法原理
假设图为 G，顶点集合为 V，边的集合为 E，按照「普里姆（Prim）」算法求解「最小生成树」的步骤如下所示：
（1）初始化 Vp = { start }，start 表示集合 V 中任意一点，表示从 start 出发构建最小生成树，Ep = {}，边的集合初始化为空，其中 Vp，Ep 表示构建过程中的顶点和边的集合；
（2）选取集合 E 中的权值最小的边 （u, v）（如果存在多个，可任选择一个），其中 u ∈ Vp，v ∈ V 且 v ∉ Vp。
（3）将 v 加入到集合 Vp 中，将 （u, v）加入到集合 Ep 中。
（4）重复（2）（3）步骤，直到集合 V = Vp 或无法找到新的顶点加入集合 Vp 为止。
（5）如果 V = Vp 说明「图G」可以找到「最小生成树」，图是连通的，否则说明图不是连通的，无法找到「最小生成树」。
2.2 实例演示
下面通过一个实例演示进行说明，假设无向「图G」如下所示。
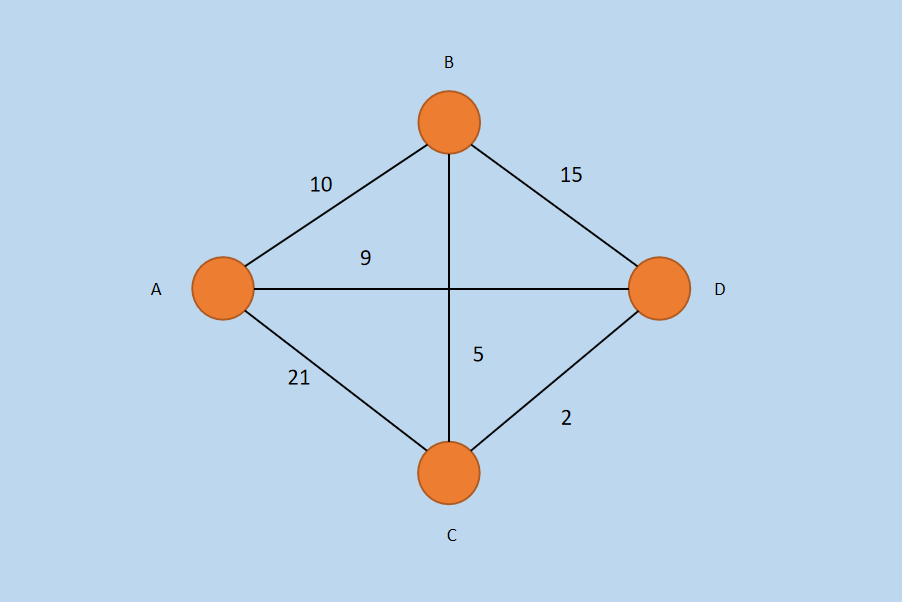图1 图 G
在上图中，包括四个顶点 A、B、C、D 以及相互连接的边，各个边上的数字表示边的权重，上面是一个无向图。
其中，V = {A, B, C, D}, E = {AB, AC, AD, BC, BD, CD}。
（1）初始时 Vp = {A}，这里设 A 是初始顶点， Ep = {}，初始化后「图G」如下所示。
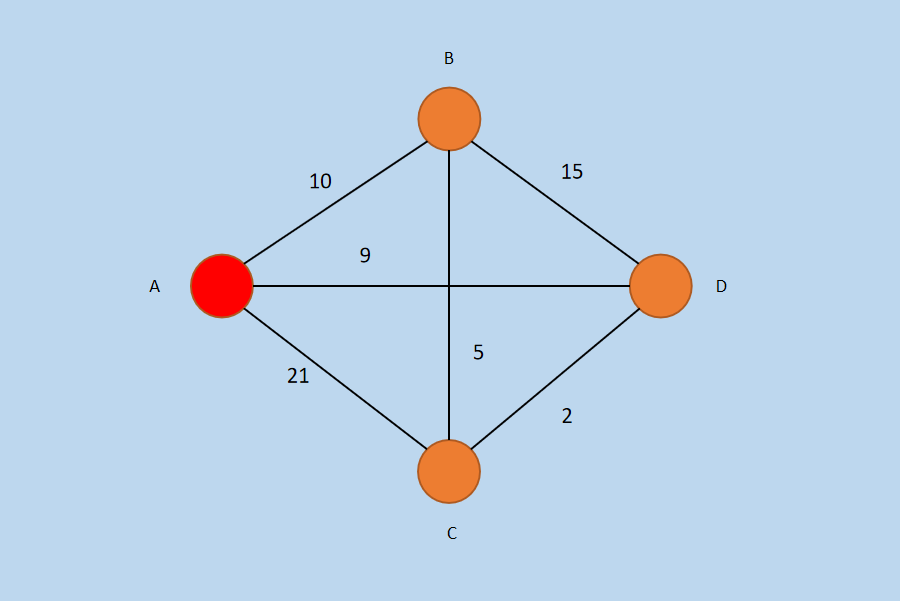图2 初始化
注意：红色的顶点或边表示已被选入到集合 Vp 和 Ep 中的顶点和边。
在经过初始化后，顶点 A 已经加入到集合 Vp 中，但是，Ep 还是为空，即：Vp = {A}，Ep = {}。
（2）选择一条符合条件的最小权值的边（u, v），符合条件的边包括 AB，AC，AD，因为要求选择的边（u, v）应满足 u ∈ Vp，v ∈ V 且 v ∉ Vp。
所以选择边 AD（因为边 AB、AC、AD的权重为分别为 10，21，9，最小的为 AD），选择 AD 后，新的图如下所示。
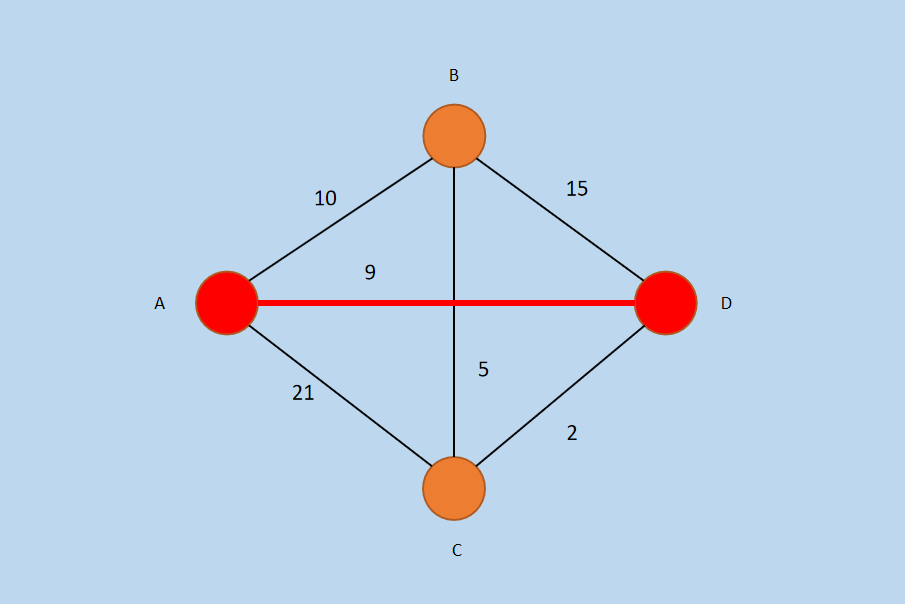图3 选择边 AD
此时，Vp = {A, D}, Ep = {AD}。
（3）再次选择一条符合条件的最小权值的边（u, v），符合条件的边包括 AB，AC, DB, DC，其中，权值最小的边为 DC，所以选择 DC。
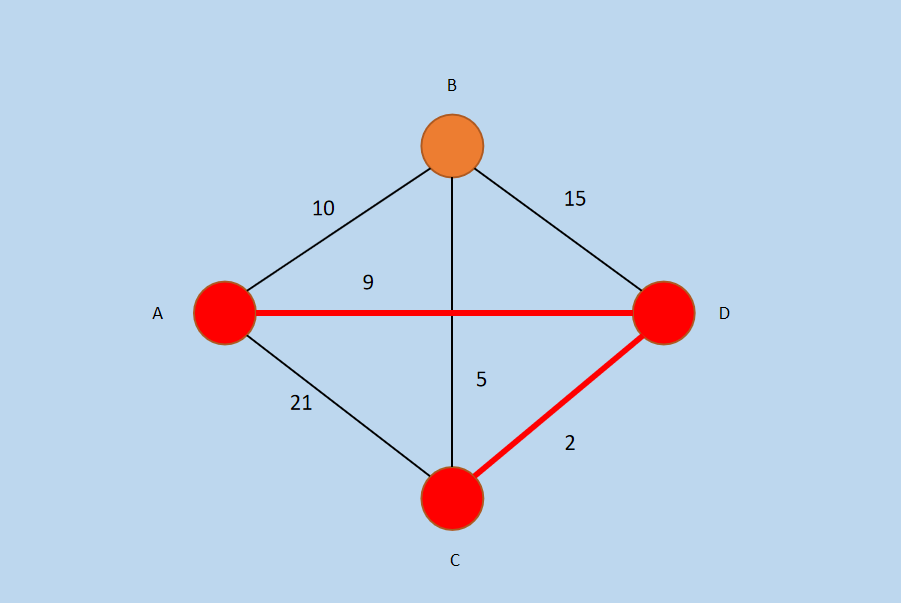图4 选择边 DC 后
新的集合为：Vp = {A, D, C}，Ep = {AD, DC}。
（4）再次选择一条符合条件的最小权值边（u，v）,符合条件的边包括 AB，CB, DB，其中，权值最小的边为 CB，所以选择 CB。
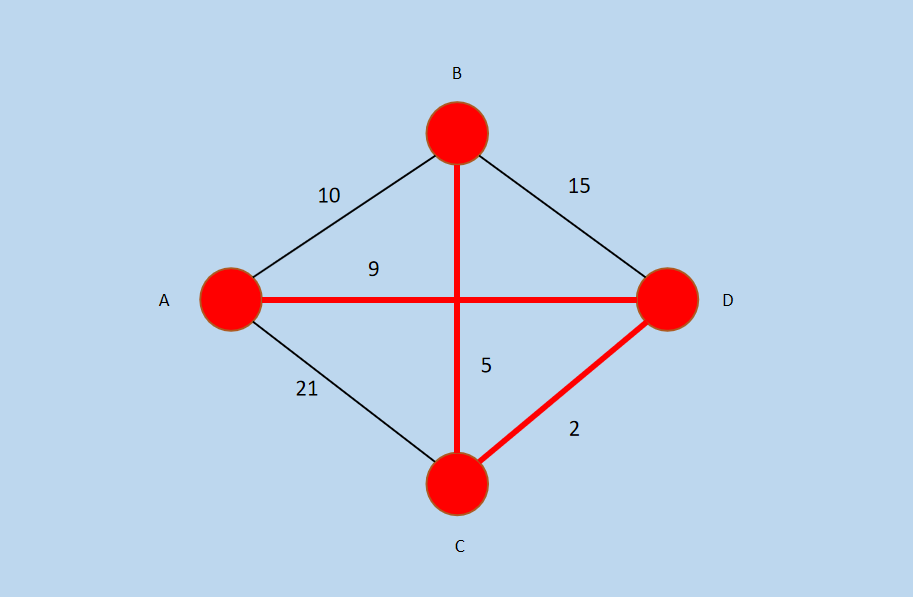图5 选择边 CB 后
新的集合为：Vp = {A, D, C, B }，Ep = {AD, DC, CB}。
经过步骤（4）后，图中所有顶点都已选完，通过 3 个边连接，此时，最小生成树如下所示。
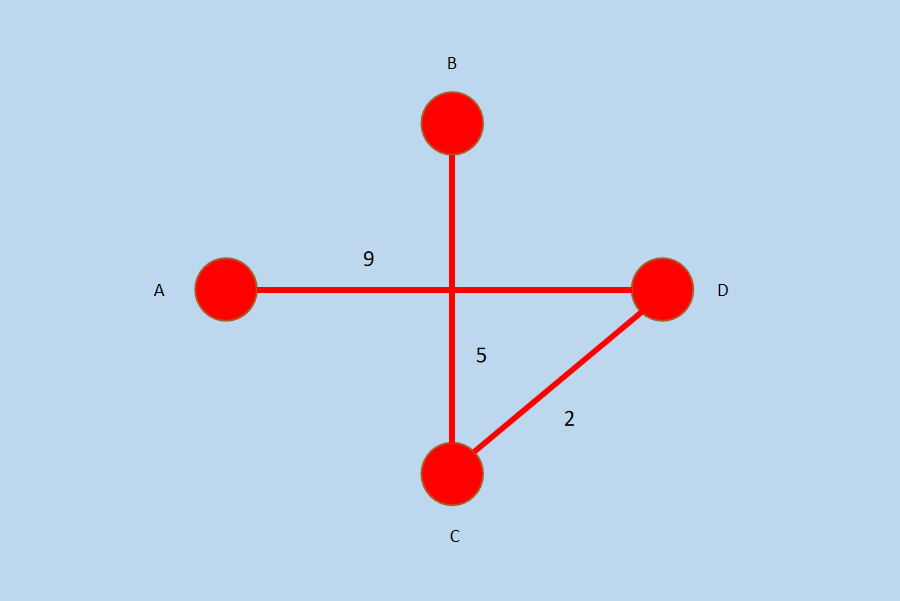图6 图 G 的最小生成树
「图G」的最小生成树的权值和为 9 + 5 + 2 = 16。
2.2 算法实现
-
#include<stdio.h>
-
#include<string.h>
-
#define INF 0x3f3f3f3f
-
#define SIZE 1e2
-
bool vis[SIZE];
-
int low[SIZE], mp[SIZE][SIZE];
-
-
/**
-
* init 初始化函数
-
*/
-
void init(int n) {
-
//初始化 vis, mp
-
memset(vis, false, sizeof(vis));
-
memset(mp, 0, sizeof(mp));
-
//初始化到自己的边
-
for(int i = 1; i <= n; ++i) {
-
mp[i][i] = INF;
-
}
-
}
-
-
/**
-
* Prim 算法
-
* n 顶点个数
-
* start 起始顶点
-
*/
-
-
int prim(int n, int start)
-
{
-
// 以 start 为起点初始化 low
-
for(int i = 1; i <= n; ++i)
-
low[i] = mp[start][i];
-
//标记 start 点已访问
-
vis[start] = true;
-
-
int num = 1; //记录有多少顶点已加入到 Vp 集合，初始时只有 start 一个顶点
-
//选择剩余的 n - 1 个顶点
-
for(int i = 2; i <= n; ++i) {
-
int idx = -1, Min = INF;
-
//寻找最小边，实际上是选择一个不在 Vp 中的顶点
-
for(int j = 1; j <= n; ++j)
-
if(!vis[j] && low[j] < Min) {
-
//记录最小边
-
idx = j;
-
Min = low[j];
-
}
-
//记录总的权值和
-
ans += Min;
-
//表示没有边可以选择
-
if(idx == -1)
-
break;
-
//Vp 中顶点加 1
-
num++;
-
//标记选出的顶点
-
vis[idx] = true;
-
//更新 low，因为选入 idx 顶点后，low 数组可能会有更新
-
for(int k = 1; k <= n; ++k) {
-
if(!vis[k] && low[k] > mp[idx][k]) {
-
low[k] = mp[idx][k];
-
}
-
}
-
}
-
return num == n ? ans : -1;
-
}
在上述代码中，二维矩阵 mp 用于存储图，low 用于记录最小权值的边，vis 标记图中顶点是否已经加入到 Vp 中。
在 prim 函数中，先以 start 为起点初始化 low 数组，此时记录的是从 start 出发到达其余顶点的距离。num 记录集合 Vp 中顶点的个数。然后，通过 for 循环遍历依次选出剩余的 n - 1 个顶点。
2.3 算法复杂度
2.3.1 时间复杂度
时间复杂度：O(n^2)，n 表示的是顶点个数，在上述算法中，两层嵌套 for 循环的时间复杂度为 O(n^2)。
2.3.2 空间复杂度
空间复杂度：O(n^2)，在上述算法中，空间复杂度主要在于图的存储，当然，可以使用「邻接表」存储。
🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶
三、最小生成树实践
理解了「普里姆（Prim）」算法后，可以练习下下面两个题目。
3.1 Agri-Net
3.2 Truck History
🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶
四、总结
「最小生成树」算法主要用于求解连通图最小权值的情况，而 「普里姆（Prim）」算法用于稠密图的情况，因为「普里姆（Prim）」算法是以顶点为基础构造「最小生成树」的。
🎈 感觉有帮助记得「一键三连」支持下哦！有问题可在评论区留言💬，感谢大家的一路支持！🤞猿哥将持续输出「优质文章」回馈大家！🤞🌹🌹🌹🌹🌹🌹🤞
文章来源: blog.csdn.net，作者：Linux猿，版权归原作者所有，如需转载，请联系作者。
原文链接：blog.csdn.net/nyist_zxp/article/details/123447704
- 点赞
- 收藏
- 关注作者
评论（0）