用Python计算样本方差，总体方差，比较

1.样本方差

#样本方差，考虑自由度

def f_sigma(x):
    # 通过Python定义一个计算变量波动率的函数
    # x：代表变量的样本值，可以用列表的数据结构输入
    n = len(x)
    u_mean = sum(x)/n  #计算变量样本值的均值
    z = []   #生成一个空列表
    for t in range(n):
        z.append((x[t]-u_mean)**2)
    return (sum(z)/(n-1))**0.5    # n-1 自由度

a = f_sigma(x = [1,2,3])
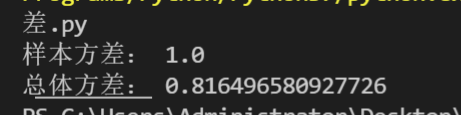
print('样本方差：', a) 

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
 

2.总体方差

#总体方差，总体个数

def f_sigma(x):
    # 通过Python定义一个计算变量波动率的函数
    # x：代表变量的样本值，可以用列表的数据结构输入
    n = len(x)
    u_mean = sum(x)/n  #计算变量样本值的均值
    z = []   #生成一个空列表
    for t in range(n):
        z.append((x[t]-u_mean)**2)
    return (sum(z)/n)**0.5    # n 总体个数

a = f_sigma([1,2,3])
print('总体方差：', a) 

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
 

3.两者区别

#样本方差，考虑自由度

def f_sigma(x):
    # 通过Python定义一个计算变量波动率的函数
    # x：代表变量的样本值，可以用列表的数据结构输入
    n = len(x)
    u_mean = sum(x)/n  #计算变量样本值的均值
    z = []   #生成一个空列表
    for t in range(n):
        z.append((x[t]-u_mean)**2)
    return (sum(z)/(n-1))**0.5    # n-1 自由度

a = f_sigma(x = [1,2,3])
print('样本方差：', a) 


#总体方差，总体个数

def f_sigma(x):
    # 通过Python定义一个计算变量波动率的函数
    # x：代表变量的样本值，可以用列表的数据结构输入
    n = len(x)
    u_mean = sum(x)/n  #计算变量样本值的均值
    z = []   #生成一个空列表
    for t in range(n):
        z.append((x[t]-u_mean)**2)
    return (sum(z)/n)**0.5    # n 总体个数

a = f_sigma([1,2,3])
print('总体方差：', a) 

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
 

文章来源: blog.csdn.net，作者：yk 坤帝，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/qq_45803923/article/details/123498874