MATLAB基础学习笔记02:掌握MATLAB运算
【摘要】
文章目录
一、算术运算(一)算术运算符(二)案例演示1、算术加减乘运算2、算术除运算3、乘方运算(1)算术乘方运算(2)矩阵点乘方运算
4、矩阵左除运算5、矩阵乘法6、矩阵点乘7、矩阵点除...
一、算术运算
(一)算术运算符
| 运算符 | 定义 |
|---|---|
| + | 算术加 |
| - | 算术减 |
| * | 算术乘 |
| .* | 点乘 |
| ^ | 算术乘方 |
| .^ | 点乘方 |
| \ | 算术左除 |
| .\ | 点左除 |
| / | 算术右除 |
| ./ | 点右除 |
' |
矩阵转置。当矩阵是复数时,求矩阵的共轭转置 |
.' |
矩阵转置。当矩阵是复数时,不求矩阵的共轭转置 |
(二)案例演示
1、算术加减乘运算

2、算术除运算

3、乘方运算
(1)算术乘方运算
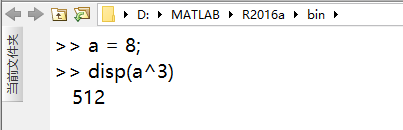
(2)矩阵点乘方运算
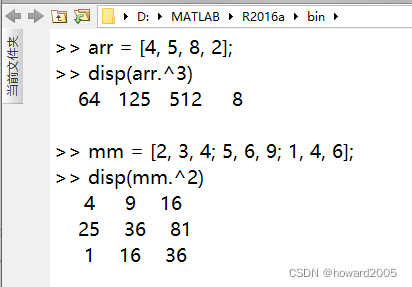
4、矩阵左除运算
- 求解线性方程组: { x + 2 y + 3 z = 14 ( 1 ) 2 x − 4 y + z = − 3 ( 2 ) 3 x + 5 y − 2 z = 7 ( 3 ) {x+2y+3z=14(1)2x−4y+z=−3(2)3x+5y−2z=7(3)
⎩⎪⎨⎪⎧x+2y+3z=142x−4y+z=−33x+5y−2z=7(1)(2)(3)
A = [ 1 2 3 2 − 4 1 3 5 − 2 ] A=\left[ 1232−4135−2
- 线性方程组表示为 A X = B AX=B AX=B,即- [ 1 2 3 2 − 4 1 3 5 − 2 ] \left[ 1232−4135−2
\right] ⎣⎡1232−4531−2⎦⎤ [ x y z ] \left[ xyz\right] ⎣⎡xyz⎦⎤ = [ 14 − 3 7 ] =\left[ 14−37\right] =⎣⎡14−37⎦⎤
- X = A − 1 B X=A^{-1}B X=A−1B相当于 X = B ÷ A X=B\div A X=B÷A,是左除

- 所以方程组的解: X = [ 1 2 3 ] X=\left[ 123
\right] X=⎣⎡123⎦⎤
5、矩阵乘法
- A = [ a i j ] , 1 ≤ i ≤ m , 1 ≤ j ≤ k A=[a_{ij}], 1\le i\le m, 1\le j\le k A=[aij],1≤i≤m,1≤j≤k
- B = [ b i j ] , 1 ≤ i ≤ k , 1 ≤ j ≤ n B=[b_{ij}], 1\le i\le k, 1\le j\le n B=[bij],1≤i≤k,1≤j≤n
- C = A × B = [ c i j ] = [ ∑ p = 1 k a i p ⋅ b p j ] , 1 ≤ i ≤ m , 1 ≤ j ≤ n \displaystyle C=A\times B=[c_{ij}]=[\sum_{p=1}^k a_{ip}\cdot b_{pj}], 1\le i\le m, 1\le j\le n C=A×B=[cij]=[p=1∑kaip⋅bpj],1≤i≤m,1≤j≤n

- A ∗ B A * B A∗B的第一个元素 25 = 1 × 3 + 2 × 5 + 3 × 4 25 = 1\times3+2\times 5+ 3\times4 25=1×3+2×5+3×4
6、矩阵点乘
- 矩阵点乘意味着对应元素相乘

7、矩阵点除
- 矩阵点除意味着对应元素相除

文章来源: howard2005.blog.csdn.net,作者:howard2005,版权归原作者所有,如需转载,请联系作者。
原文链接:howard2005.blog.csdn.net/article/details/123437630
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者






评论(0)