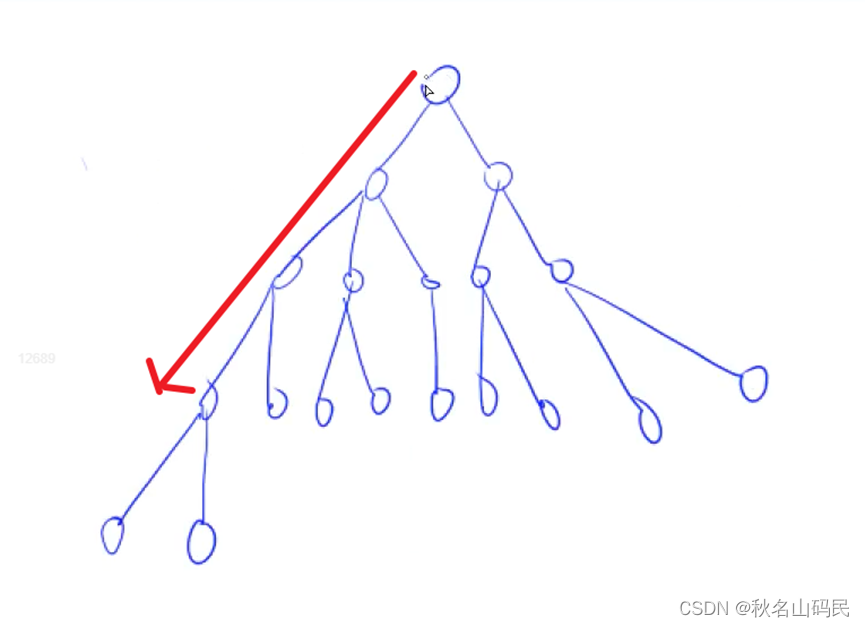
从每个节点一条路走下去，直到走不通为止

dfs全排列问题

以三为例，dfs的搜索顺序如下图所示

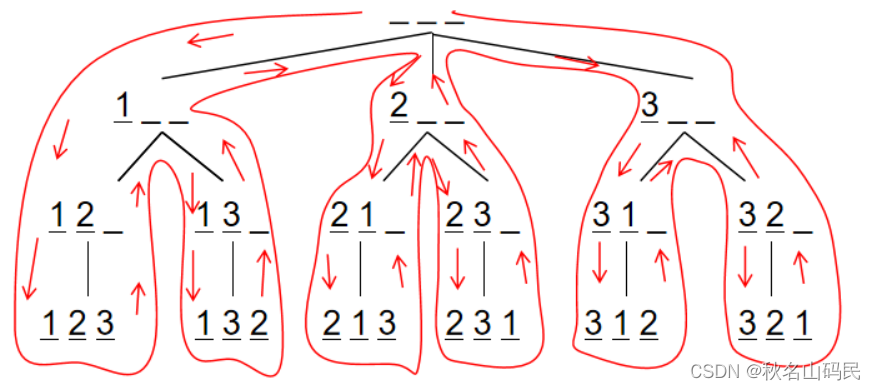
#include<iostream>
using namespace std;
const int N = 10;
int path[N];//保存序列
int state[N];//数字是否被用过
int n;
void dfs(int u)
{
    if(u > n)//数字填完了，输出
    {
        for(int i = 1; i <= n; i++)//输出方案
            cout << path[i] << " ";
        cout << endl;
    }

    for(int i = 1; i <= n; i++)//空位上可以选择的数字为:1 ~ n
    {
        if(!state[i])//如果数字 i 没有被用过
        {
            path[u] = i;//放入空位
            state[i] = 1;//数字被用，修改状态
            dfs(u + 1);//填下一个位
            state[i] = 0;//回溯，取出 i
        }
    }
}

int main()
{

    cin >> n;
    dfs(1);
}

dfs N皇后问题

n皇后

「N 皇后问题」研究的是如何将 N 个皇后放置在 N×N 的棋盘上，并且使皇后彼此之间不能相互攻击。
皇后的走法是：可以横直斜走，格数不限。因此要求皇后彼此之间不能相互攻击，等价于要求任何两个皇后都不能在同一行、同一列以及同一条斜线上。

直观的做法是暴力枚举将 N个皇后放置在 N×N 的棋盘上的所有可能的情况，并对每一种情况判断是否满足皇后彼此之间不相互攻击。

对应今天的主题，我们就先用dfs深搜的方式来写这个n皇后问题

思路：
显然，每个皇后必须位于不同行和不同列，因此将 N 个皇后放置在 N ×N 的棋盘上，一定是每一行有且仅有一个皇后，每一列有且仅有一个皇后，且任何两个皇后都不能在同一条斜线上。

具体做法：
使用一个数组记录每行放置的皇后的列下标，依次在每一行放置一个皇后。每次新放置的皇后都不能和已经放置的皇后之间有攻击：即新放置的皇后不能和任何一个已经放置的皇后在同一列以及同一条斜线上，并更新数组中的当前行的皇后列下标。当 N 个皇后都放置完毕，则找到一个可能的解。当找到一个可能的解之后，将数组转换成表示棋盘状态的列表，并将该棋盘状态的列表加入返回列表。

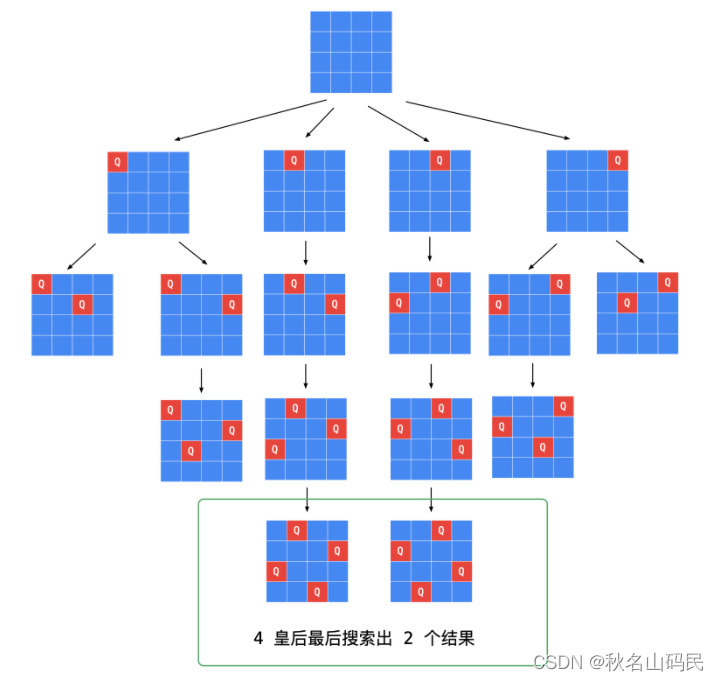
#include <iostream>
using namespace std;
const int N = 20; 

// bool数组用来判断搜索的下一个位置是否可行
// col列，dg对角线，udg反对角线
// g[N][N]用来存路径

int n;
char g[N][N];
bool col[N], dg[N], udg[N];

void dfs(int u) {
    //搜到
    if (u == n) {
        for (int i = 0; i < n; i ++ ) puts(g[i]);   
        puts(""); 
        return;
    }

    //对n个位置按行搜索
    for (int i = 0; i < n; i ++ )
        // 剪枝(对于不满足要求的点，不再继续往下搜索)  
        // udg[n - u + i]，+n是为了保证下标非负
        if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
            g[u][i] = 'Q';
            col[i] = dg[u + i] = udg[n - u + i] = true;
            dfs(u + 1);
            col[i] = dg[u + i] = udg[n - u + i] = false; // 恢复现场 
            g[u][i] = '.';
        }
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0);

    return 0;
}   

最长快乐字符串

int used;
char GetNext(int *a, int *b, int *c)
{
    int m = *a, n = *b, p = *c;
    if (used == 1) { /* 哪个用过了，不参与比较 */
        m = 0;
    }
    if (used == 2) {
        n = 0;
    }
    if (used == 3) {
        p = 0;
    }
    if ((m >= n) && (m >= p) && (m > 0)) {
        (*a)--;
        used = 0;
        return 'a';
    }
    if ((n >= m) && (n >= p) && (n > 0)) {
        (*b)--;
        used = 0;
        return 'b';
    }
    if ((p >= m) && (p >= n) && (p > 0)) {
        (*c)--;
        used = 0;
        return 'c';
    }
    return '0';
}
char * longestDiverseString(int a, int b, int c)
{
    used = 0;
    char *res = calloc(a + b + c + 1, sizeof(char));
    char t;
    int cnt = 0;
    while (true) {
        t = GetNext(&a, &b, &c);
        if (t != '0') {
            res[cnt++] = t; 
        } else {
            break;
        }
        if ((cnt >= 2) && (res[cnt - 2] == 'a') && (res[cnt - 1] == 'a')) {
            used = 1;
        }
        if ((cnt >= 2) && (res[cnt - 2] == 'b') && (res[cnt - 1] == 'b')) {
            used = 2;
        }
        if ((cnt >= 2) && (res[cnt - 2] == 'c') && (res[cnt - 1] == 'c')) {
            used = 3;
        }
    }
    return res;
}

二叉树的最近祖先

dfs二叉树的最近祖先
值得注意：一个节点也可以是它自己的祖先，二叉搜索树，对于根节点来说，左边比根小，右边比根大，可以做截枝

暴搜

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //if (root == p || root == q) return root;
        if (p->val < root->val && q->val < root->val) return lowestCommonAncestor(root->left, p, q);
        if (p->val > root->val && q->val > root->val) return lowestCommonAncestor(root->right, p, q);
        return root;
    }
};

class Solution {
public:
    vector<TreeNode*> getPath(TreeNode* root, TreeNode* target) {
        vector<TreeNode*> path;
        TreeNode* node = root;
        while (node != target) {
            path.push_back(node);
            if (target->val < node->val) {
                node = node->left;
            }
            else {
                node = node->right;
            }
        }
        path.push_back(node);
        return path;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        vector<TreeNode*> path_p = getPath(root, p);
        vector<TreeNode*> path_q = getPath(root, q);
        TreeNode* ancestor;
        for (int i = 0; i < path_p.size() && i < path_q.size(); ++i) {
            if (path_p[i] == path_q[i]) {
                ancestor = path_p[i];
            }
            else {
                break;
            }
        }
        return ancestor;
    }
};

bfs

广度优先搜索，像下面这张图一样，一层一层去搜索，我们也不难看出，当边的权值都是一样的时候，第一次搜索就是最短路，后面的搜索都比第一次大，引出最短路问题，这个我们后面再说。

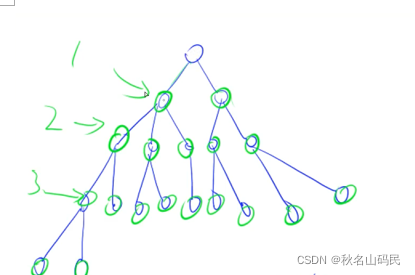
迷宫
dfs保证搜到终点，但是不能保证搜到的是最短的

#include<bits/stdc++.h>//万能头文件
using namespace std;
const int MAXSIZE_N=1000;
const int MAXSIZE_M=100000;
struct state{
    int x;
    int y;
};//养成好习惯~结构体有利于我们调整程序

bool IsUsed[MAXSIZE_N][MAXSIZE_N];//记录迷宫bfs的遍历状态
bool maze[MAXSIZE_N][MAXSIZE_N];//maze用于记录迷宫本身
int lookUpTable[MAXSIZE_N][MAXSIZE_N]={0};//建立查询表，记忆化搜索

int n,m;
int cnt=0;//记录可走的格子数

state dir[4]={{1,0},{-1,0},{0,1},{0,-1}};

void InitAll()
{
//    memcpy(maze,neverMaze,sizeof(neverMaze));
//    memcpy(IsUsed,neverUsed,sizeof(neverUsed));//速度过慢
    cnt=0;
}

bool IsSafe(state now,state next)
{
    return(next.x>=0&&next.x<n&&next.y>=0&&next.y<n)//在范围内
    &&(maze[next.x][next.y]!=maze[now.x][now.y])//题目定义的规则,只能0->1或1->0
    &&(IsUsed[next.x][next.y]!=true);//没有染过色or没走过
}


void bfs(state start)
{
    queue<state> Q;
    queue<state> memoryPos;//用于记忆化搜索，记录走过的点，提高速度
    IsUsed[start.x][start.y]=true;
    cnt++;
    Q.push(start);
    memoryPos.push(start);
    while(!Q.empty()){
        state now=Q.front();
        Q.pop();
        for(int i=0;i<4;i++){
            state next=now;
            next.x+=dir[i].x;
            next.y+=dir[i].y;
            if(IsSafe(now,next)){
                IsUsed[next.x][next.y]=true;
                memoryPos.push(next);
                cnt++;
                Q.push(next);
            }
        }
    }
    while(!memoryPos.empty())
    {
        state next=memoryPos.front();
        //把走过的点都记到表中
        memoryPos.pop();
        lookUpTable[next.x][next.y]=cnt;
    }
}

int main()
{
    std::ios::sync_with_stdio(false);//加快输入流的速度
    cin>>n>>m;
    string in[n];
    state start[m];
    for(int i=0;i<n;i++)    cin>>in[i];
    for(int i=0;i<m;i++){
        cin>>start[i].x>>start[i].y;
        start[i].x-=1;//调整输入的坐标到从零开始的坐标
        start[i].y-=1;
    }

    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            if(in[i][j]=='0')
                maze[i][j]=false;//输入的0记为false
            else
                maze[i][j]=true;//1记为true
        }
    }

    for(int i=0;i<m;i++)
    {
        if(lookUpTable[start[i].x][start[i].y]!=0){
            cout<<lookUpTable[start[i].x][start[i].y]<<'\n';//建立查询表
            continue;
        }

        InitAll();//开始是用memcpy初始化IsUsed的..后来发现染色法其实根本不需要重新初始化，但还是保留了函数
        bfs(start[i]);//对每个输入的点进行bfs
        cout<<cnt<<'\n';
    }
    return 0;
}