一、求 $e^{j{\omega }_{0}n}$ 傅里叶变换

求 $e^{j{\omega }_{0}n}$ 的傅里叶变换 $SFT[e^{j{\omega }_{0}n}]$ ?

1、傅里叶变换与反变换公式介绍

傅里叶变换 : 时域 " 离散非周期 " 信号 , 其频域就是 " 连续周期 " 的 , 其频域 可以 展开成一个 " 正交函数的无穷级数加权和 " , 如下公式

$$X(e^{j\omega })=\sum _{n=-\infty }^{+\infty }x(n)e^{-j\omega n}$$

傅里叶反变换 : 利用 " 正交函数 " 可以推导出 " 傅里叶反变换 " , 即 根据 傅里叶变换 推导 序列 ;

$$x(n)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }X(e^{j\omega })e^{j\omega k}d\omega$$

2、带入 傅里叶变换 公式

将

$$e^{j{\omega }_{0}n}$$

序列函数 , 带入到 傅里叶变换 公式

$$X(e^{j\omega })=\sum _{n=-\infty }^{+\infty }x(n)e^{-j\omega n}$$

中 ;

可以得到 :

$$SFT[e^{j{\omega }_{0}n}]=\sum _{n=-\infty }^{+\infty }{e}^{j{\omega }_{0}n}{e}^{-j\omega n}$$

根据指数运算法则 , 可以得到如下式子 :

$$SFT[e^{j{\omega }_{0}n}]=\sum _{n=-\infty }^{+\infty }{e}^{-j(\omega -{\omega }_0)}①$$

在上一篇博客 【数字信号处理】序列傅里叶变换 ( 基本序列的傅里叶变换 | 求 1 的傅里叶变换 ) 中 , 求 $1$ 的傅里叶变换得到如下公式 :

$$X(e^{j\omega })=\sum _{n=-\infty }^{+\infty }{e}^{-j\omega n}=2\pi \tilde{\delta }(\omega )②$$

将 ② 带入到 ① 中 ,

$$SFT[e^{j{\omega }_{0}n}]=\sum _{n=-\infty }^{+\infty }{e}^{-j(\omega -{\omega }_0)}=2\pi \tilde{\delta }(\omega -{\omega }_0)$$

其中 $\tilde{\delta }(\omega )$ 序列如下 , 这是以 $2\pi$ 为周期的单位脉冲序列 , 在 $2\pi$ 整数倍的位置上值为 $1$ ;

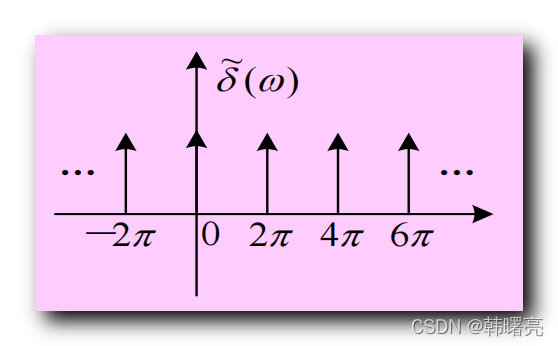
$\tilde{\delta }(\omega )$ 可以写成如下式子 :

$$\tilde{\delta }(\omega )=\sum _{m=-\infty }^{\infty }\delta (\omega -2\pi m)$$

$m$ 取值 $(-\infty ,+\infty )$ ;

文章来源: hanshuliang.blog.csdn.net，作者：韩曙亮，版权归原作者所有，如需转载，请联系作者。

原文链接：hanshuliang.blog.csdn.net/article/details/123360738