一、单位脉冲序列 傅里叶变换

求 单位脉冲序列 $\delta (n)$ 的傅里叶变换 :

傅里叶变换公式 : 根据 $x(n)$ 序列 求 $X(e^{j\omega })傅里叶变换$ ,

$$X(e^{j\omega })=\sum _{n=-\infty }^{+\infty }x(n)e^{-j\omega n}$$

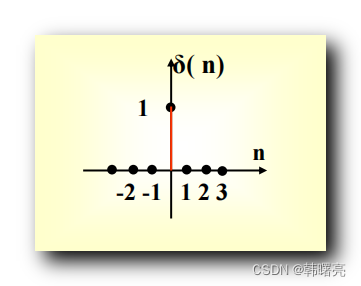
单位脉冲函数 ( 单位冲击函数 ) 对应的 函数图像 如下 : 横轴是 $n$ , 纵轴是 $\delta (n)$ ;

• $n=0$ 时 , $\delta (n)=1$
• $n=1$ 时 , $\delta (n)=0$
  

将 $\delta (n)$ 带入到 傅里叶变换 公式中 ,

• 当 $n$ 不为 $0$ 时 , $\delta (n)=0$ , 这些项都是 $0$ ;
• 当 $n=0$ 时 , $\delta (n)e^{-j\omega n}=1$ ;

最终 :

$$SFT[\delta (n)]=\sum _{n=-\infty }^{+\infty }\delta (n)e^{-j\omega n}=1$$

文章来源: hanshuliang.blog.csdn.net，作者：韩曙亮，版权归原作者所有，如需转载，请联系作者。

原文链接：hanshuliang.blog.csdn.net/article/details/123337289