【数字信号处理】相关函数应用 ( 正弦信号 的 自相关函数 分析 二 | 在白噪声中检测正弦信号 )
文章目录
一、正弦信号 的 自相关函数 分析
正弦信号 s ( n ) = A sin ω n s(n) = A \sin \omega n s(n)=Asinωn ,
其 幅度 A = 3.166 A = 3.166 A=3.166 , 功率 P s = 5.01 P_s = 5.01 Ps=5.01 , 信号长度为 512 512 512 ;
下图是该正弦信号的函数图 :
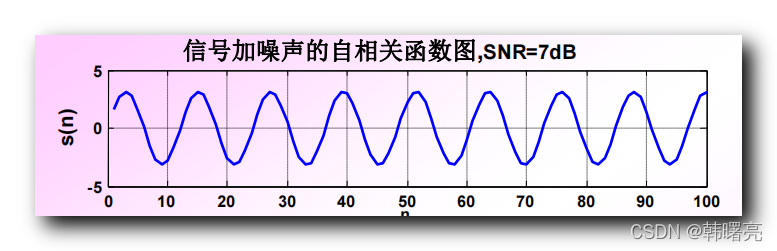
白噪声信号 N ( n ) N(n) N(n) , 方差 1 1 1 , 信噪比 S N R = 7 d B \rm SNR = 7dB SNR=7dB , 信号长度为 512 512 512 ;
下图是 正弦信号 s ( n ) = A sin ω n s(n) = A \sin \omega n s(n)=Asinωn 与 白噪声信号 N ( n ) N(n) N(n) 叠加后的 函数图 :
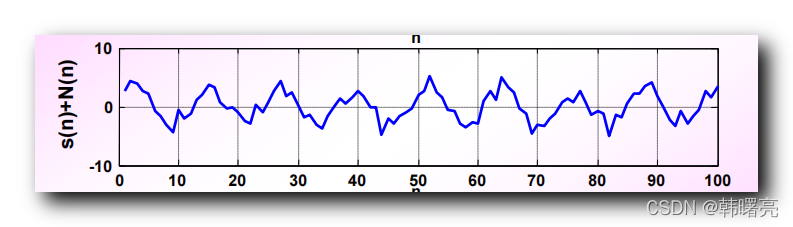
从上图中 , 可以大概分辨出信号 , 比上一篇博客 【数字信号处理】相关函数应用 ( 正弦信号 的 自相关函数 分析 | 在白噪声中检测正弦信号 ) 中 , 叠加后的信号 明显很多 , 下图是上一篇博客中叠加后的信号 :
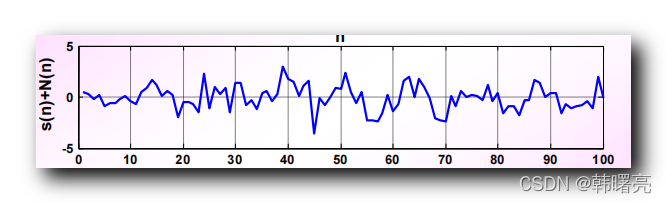
上图的叠加信号 , 基本无法辨识 ;
求 正弦信号 s ( n ) = A sin ω n s(n) = A \sin \omega n s(n)=Asinωn 与 白噪声信号 N ( n ) N(n) N(n) 叠加后 的信号的 相关函数 r ( m ) r(m) r(m) , 可以得到如下的函数图 :
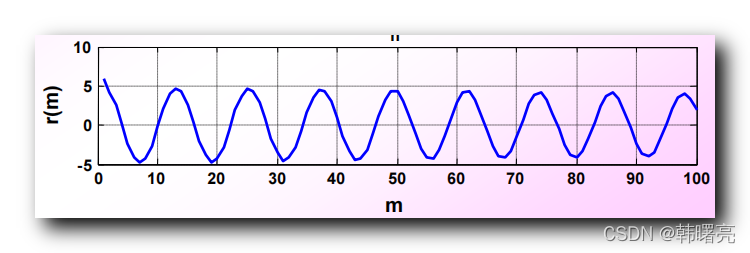
在 自相关函数 r ( m ) r(m) r(m) 中的 m = 0 m = 0 m=0 点处 , 相关性很大 , 此处是
信 号 功 率 + 噪 声 功 率 = 6.01 信号功率 + 噪声功率 = 6.01 信号功率+噪声功率=6.01
信号功率是 5.01 5.01 5.01 , 噪声的功率是 1 1 1 ,
在 m = 0 m = 0 m=0 处 , 白噪声的功率是 1 1 1 , 信号的功率是 5.01 5.01 5.01 ;
在其它地方 m ≠ 0 m \not= 0 m=0 时 , 白噪声功率趋近于 0 0 0 , 只剩下 信号功率了 , 这样实现了在 噪声中 检测 信号 ;
信号的功率越大 , 越容易识别噪声中的信号 ;
文章来源: hanshuliang.blog.csdn.net,作者:韩曙亮,版权归原作者所有,如需转载,请联系作者。
原文链接:hanshuliang.blog.csdn.net/article/details/123249724
- 点赞
- 收藏
- 关注作者


评论(0)