以下为我的天梯积分规则：

每日至少一题：一题积分+10分
若多做了一题（或多一种方法解答），则当日积分+20分（+10+10）
若做了三道以上，则从第三题开始算+20分（如：做了三道题则积分-10+10+20=40；做了四道题则积分–10+10+20+20=60）

---

初始分为100分
若差一天没做题，则扣积分-10分（周六、周日除外注：休息）
坚持！！！

初级算法

刷题目录

其他

题干

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例1：

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例2：

输入: numRows = 1
输出: [[1]]

法一

根据大佬的思路来一遍。

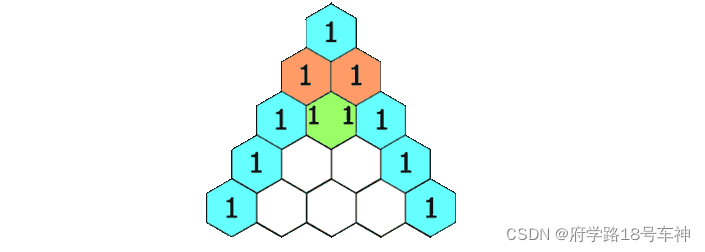
首先观察这个三角形的特点，杨辉三角形是一个等边三角形，其中左边和右边每个格子的值都是1。

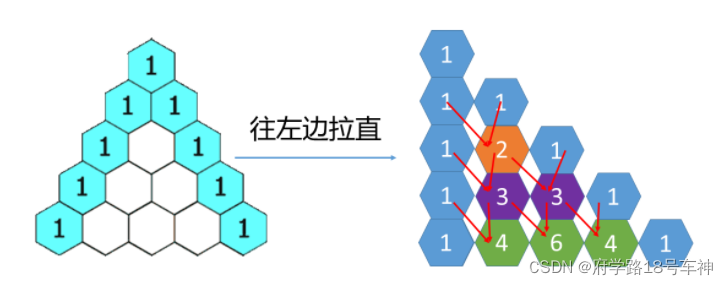
三角形斜的不好看，如果我们把这个三角形往左边拉直就会发现，除了两边的都是1以外，其他每个格子的值都是他正上面格子和左上角格子的和。

法二

每一行的元素数量等于行号（行号从1开始）
每一行的第一位和最后一位为1
每一行除首位元素之外，其余元素计算公式为：
S[i][j] = S[i - 1][j - 1] + S[i - 1][j]

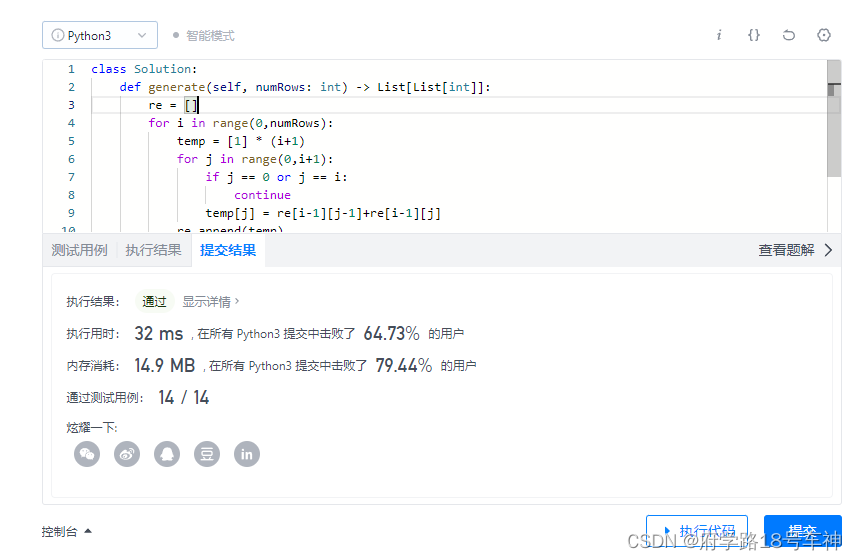
class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        re = []
        for i in range(0,numRows):
            temp = [1] * (i+1)
            for j in range(0,i+1):
                if j == 0 or j == i:
                    continue
                temp[j] = re[i-1][j-1]+re[i-1][j]
            re.append(temp)
        return re

这周太累了，天天ddl，没法了！~