复杂网络节点重要性算法之度和度中心性

度（或度中心性）是复杂网络中衡量节点重要性最直观的指标，也是最简单的节点重要性排序算法。一个节点的度值越大，则越重要。节点i 的度(Degree) 定义为该节点的邻居数目。王建伟等认为网络中节点的重要性不但与自身的信息具有一定的关系, 而且与该节点邻居节点的度也存在一定的关联, 即节点的度及其邻居节点的度越大, 节点就越重要.

一、计算网络节点的度

aij即网络邻接矩阵A中第i行第j列元素。

（1）直接调用已有函数计算

R语言代码：

#计算度  
library(igraph)   #图处理
D=degree(g);

（2）通过apply函数计算

R语言代码：

#计算度  
library(dplyr)
D<-apply(A,1,sum);

（3）遍历节点计算邻居节点个数

R语言代码：

#计算度 
D<-rep(0,n)  
for(i in 1:n){    
    D[i]=sum(A[i,])  
}

二、度中心性

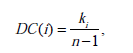
ki为节点i的度, n 为网络的节点数目, 分母n-1 为节点可能的最大度值。

R语言代码：

#参数：A--邻接矩阵，n--网络节点个数；返回值：DC--度中心性
calDC<-function(A,n){  
    #计算度    
    D<-apply(A,1,sum);  
    #计算度中心性  
    DC<-D/(n-1);  
    return (DC)
}

度中心性只是衡量节点中心性的指标之一，还有另外三个衡量节点中心性的主要指标：

接近中心性（Closeness Centrality）。反映在网络中某一节点与其他节点之间的接近程度。

中介中心性/中间中心性(Between Centrality) 。以经过某个节点的最短路径数目来刻画节点重要性的指标。

特征向量中心性（Eigenvector Centrality）。一个节点的重要性既取决于其邻居节点的数量（即该节点的度），也取决于其邻居节点的重要性。

参考文献：

汪小帆, 李翔, 陈关荣. 网络科学导论[M]. 高等教育出版社, 2012.

任晓龙, 吕琳媛. 网络重要节点排序方法综述[J]. 科学通报, 2014(13):1175-1197.