基于FPGA的双线性插值算法设计与分析
【摘要】 基于FPGA的双线性插值算法设计与分析前言1、几种常见插值类型1.1 最邻近插值1.2 双线性插值1.3 双三次插值2、FPGA实现双线性插值2.1 准备工作2.2 实现的难点2.3 整体的RTL图2.3.1 坐标转换模块2.3.1.1 双线性插值代填充坐标公式:2.3.1.2 小数部分的处理2.3.1.3 小数部分的表示2.3.1.4 系数的表示2.3.2 内存管理模块2.3.3双线性插值...
基于FPGA的双线性插值算法设计与分析
-
在视频图像几何校正或图像配准坐标系转换中,往往需要进行缩放、旋转、透视变换等几何变换操作。要想进行缩放旋转操作,就要得到输入输出图像之间的映射关系,也可称之为几何变换关系。
-
几何变换的基本结构,包括两种如下左图的前向映射和右图的逆向映射
-
-
向前映射适合于处理流输入,例如 来自一个摄像机的输入,其每个输入像素 能被映射到 指定输出图像中的位置。
-
逆向映射更适合于产生数据流输出,例如图像数据流输出到显示器,因为对于每个输出像素,逆向映射指定了 像素值来自于 输入图像的什么位置
-
地址的话,一般由行列计数器提供,通过行列计数器获得某点坐标,从而根据二维坐标到一维地址的转换地址计算得到。
-
但是按照这种映射关系,输出图像的像素可能被映射到输入图像的非整数坐标上,因此需要采用插值技术。

- 网上有很多解释,可自己查阅
- 最简单但锯齿严重
- 基本原理:选择距离期望位置最近的像素(相当于复制粘贴)
- 核心思想:分别在xy两个方向上进行一次插值。

比如下图所示,已知四个红色点的像素值且为整数,求最终落在非整数位置的P的像素值。我们可以先在x方向上进行插值,得到插值结果R1和R2,然后在y方向上继续进行插值,即可得到插值点P。
- 效果更平滑,和双线性插值类似,只不过用相邻16个点,复杂且消耗资源多。
- 一般来说,双线性插值是一个折中选择。
- 100*100的mif文件,为提前将图像数据存储在RAM中
- 用双线性插值来实现100100图像到256256图像的放大操作。
- 双线性插值公式
- 算法中小数部分到底该如何处理
- 如果求出插值公式中的系数,以及周围四个点的坐标
- 求出四个点之后,为加快速度,如何将四个点的像素值同时读出
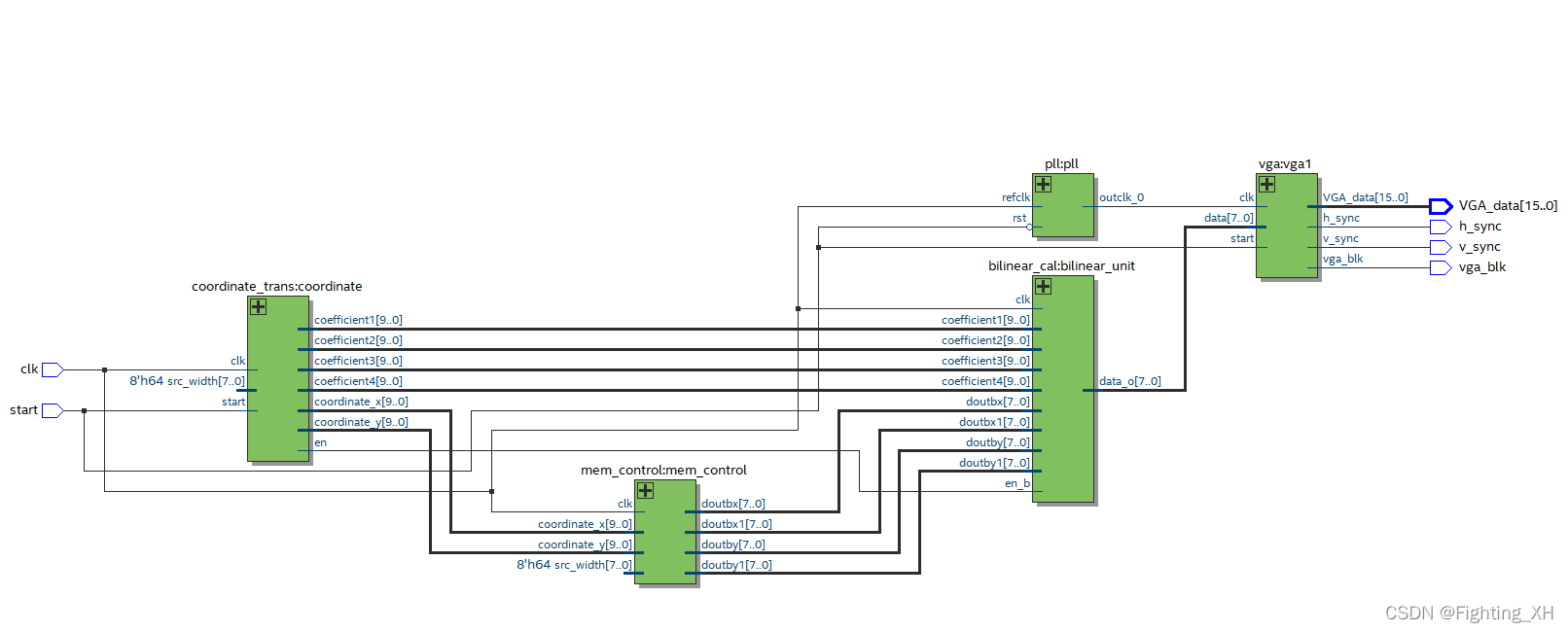
- 上图可看到,包含五个模块:坐标转换模块,内存管理模块,双线性插值计算模块,分频模块,VGA显示模块。重点看前三个模块。
- 为了解决小数部分的问题。
-
首先如下是采用最近邻实现缩放的公式:

-
为达到更好的效果,进行了如下优化

-
由此可以计算出目标像素点,对应原图像像素点的坐标。
- 我们采用扩大倍数的方式来处理小数部分,因为要100100扩大到256256,因此需要扩大512倍,才能没有小数部分,所以公式改变:
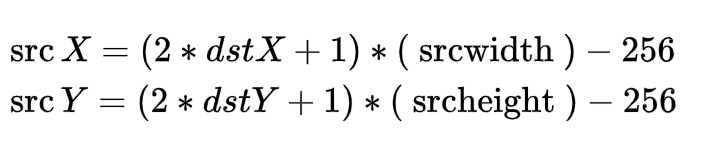
- 由于扩大到了256*256,256用9位宽表示,因此直接用20位位宽来表示srcX,Y
- 所以高10位表示整数,低10位表示小数部分。
//高10位为整数部分
assign coordinate_x = src_x[19:10];
assign coordinate_y = src_y[19:10];
//低10位为小数部分
assign coordinate_xx = src_x[9:0];
assign coordinate_yy = src_y[9:0];
- 系数包含,u,1-u,v,1-v。因为扩大了512倍数,所以1-u,变成了512-扩大后的小数部分的u
assign coefficient2 = {1'b0,src_x[8:0]}; //u
assign coefficient1 = 'd512 - coefficient2; // 1-u
assign coefficient4 = {1'b0,src_y[8:0]}; //v
assign coefficient3 = 'd512 - coefficient4; //1-v
- 采用4个RAM来解决同时读取四个点对应像素的问题
- 调用IP核的方法,将之前的mif文件存储进去即可

将系数和四个坐标代入公式
assign data_1 = coefficient1*coefficient3*doutbx; //(1-u)*(1-v)*f(i,j)
assign data_2 = coefficient2*coefficient3*doutbx1;//u*(1-v)*f(i+1,j)
assign data_3 = coefficient1*coefficient4*doutby;//(1-u)*v*f(i,j+1)
assign data_4 = coefficient2*coefficient4*doutby1;//u*1-v*f(i+1,j+1)
因为扩大了512倍数,因此还要将结果缩小512倍。所以取高8位
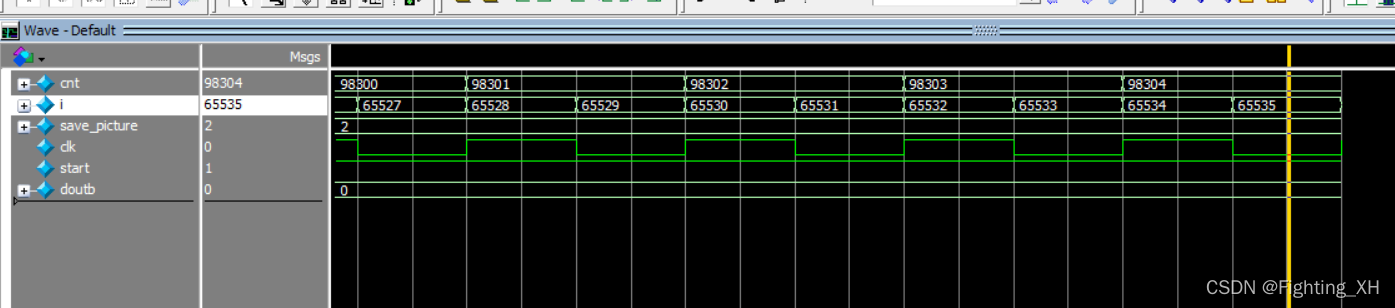
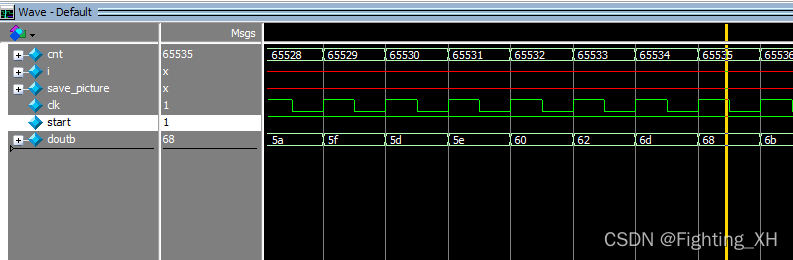
- 设计计数器,看插值图像是否完成
-可看到,最后接收65536个数据。(从0开始)
插值结果的正确性,可以用matlab或者python验证
例如,如下是我们采用matlab或者python生成的图像数据(相当于mif文件)
截取部分数据进行查看,能看到是相对应的。

依次验证也能得到该设计正确,观察波形图正确后,即可上板验证。 - 还可采用之前文章的方法,将数据从波形中导出,便于查看数据。
- always @ (posedge clk)
begin
if (!start)
j <=0;
else if (j<65535)
j <= j+1;
else
j<= 65535;
end
//如下想要将256*256图像的65536个数据导出
integer w_file;
initial w_file = $fopen("data_out.txt");
always @(j)
begin
$fdisplay(w_file,"%h",doutb); //十进制的输出
if(j == 21'd65535) ; //共写入65536个数据
end
也能生成对应的文档,其中数据与matlab或者python生成的图像数据一样,说明插值成功。
波形成功后,加入了VGA显示模块,想要直接屏幕显示效果,但目前打不开modelsim,下次再试
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


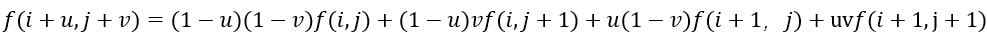
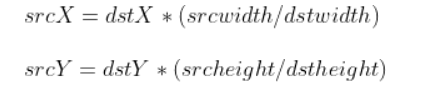
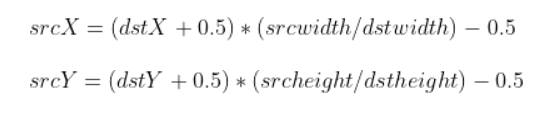



评论(0)