DSP实验报告（一）之离散时间信号和系统的时域分析

一、产生如下因果线性时不变系统的冲激响应的前45个样本并绘图：

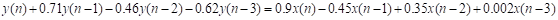
clf;
N = 45;
num = [0.9 -0.45 0.35 0.002];
den = [1 0.71 -0.46 -0.62];
y = impz(num,den,N);
% Plot the impulse response
stem(y);
xlabel('Time index n'); ylabel('Amplitude');
title('Impulse Response'); grid; 


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
 

二、对序列 和 求卷积生成 ，并用FIR滤波器 对输入 滤波，求得 ； 和 有差别吗？为什么要使用对 补零后得到的 作为输入来产生 ？

clf;
h = [3 2 1 -2 1 0 -4 0 3];	% impulse response
x = [1 -2 3 -4 3 2 1];		% input sequence
y = conv(h,x);
n = 0:14;
subplot(2,1,1);
stem(n,y);
xlabel('Time index n'); ylabel('Amplitude');
title('Output Obtained by Convolution'); grid;
x1 = [x zeros(1,8)];
y1 = filter(h,1,x1);
subplot(2,1,2);
stem(n,y1);
xlabel('Time index n'); ylabel('Amplitude');
title('Output Generated by Filtering'); grid;


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
 

两者图像没有差别。

之所以要x补零，是因为filter的原因。H共9个数，x共7个数，卷积后15个。Filter最后的结果个数是和x相等的，所以要对x补8个0，再加入filter才能得到正确的结果。

文章来源: recclay.blog.csdn.net，作者：ReCclay，版权归原作者所有，如需转载，请联系作者。

原文链接：recclay.blog.csdn.net/article/details/84672436