【数据结构与算法】之深入解析“二叉树的层序遍历”的求解思路与算法示例
【摘要】
一、题目要求
给你二叉树的根节点 root ,返回其节点值的层序遍历 (即逐层地,从左到右访问所有节点)。示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:[[...
一、题目要求
- 给你二叉树的根节点 root ,返回其节点值的层序遍历 (即逐层地,从左到右访问所有节点)。
- 示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
- 1
- 2
- 示例 2:
输入:root = [1]
输出:[[1]]
- 1
- 2
- 示例 3:
输入:root = []
输出:[]
- 1
- 2
- 提示:
-
- 树中节点数目在范围 [0, 2000] 内;
-
- -1000 <= Node.val <= 1000。
二、求解算法
① BFS 层序遍历
- DFS(深度优先搜索)和 BFS(广度优先搜索)就像孪生兄弟,提到一个总是想起另一个。然而在实际使用中,用 DFS 的时候远远多于 BFS,那么是不是 BFS 就没有什么用呢?
- 如果使用 DFS/BFS 只是为了遍历一棵树、一张图上的所有结点的话,那么 DFS 和 BFS 的能力没什么差别,我们当然更倾向于更方便写、空间复杂度更低的 DFS 遍历。不过,某些使用场景是 DFS 做不到的,只能使用 BFS 遍历,比如「层序遍历」和「最短路径」这两个场景。
- 虽然 DFS 与 BFS 都是将二叉树的所有结点遍历了一遍,但它们遍历结点的顺序不同,这个遍历顺序也是 BFS 能够用来解「层序遍历」、「最短路径」问题的根本原因:

- 什么是层序遍历呢?简单来说,层序遍历就是把二叉树分层,然后每一层从左到右遍历:
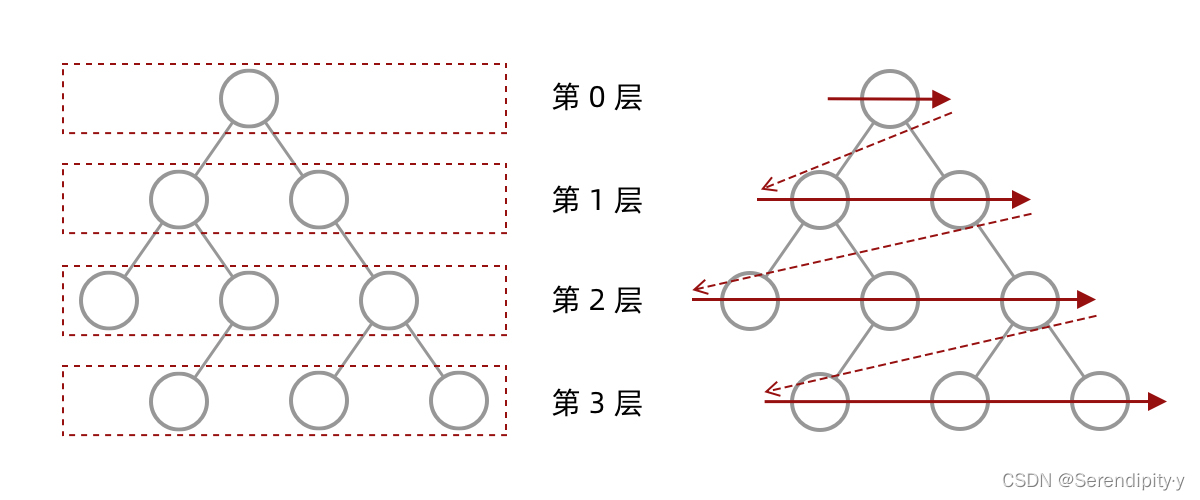
- 乍一看来,这个遍历顺序和 BFS 是一样的,可以直接用 BFS 得出层序遍历结果。然而,层序遍历要求的输入结果和 BFS 是不同的,层序遍历要求区分每一层,也就是返回一个二维数组,而 BFS 的遍历结果是一个一维数组,无法区分每一层:
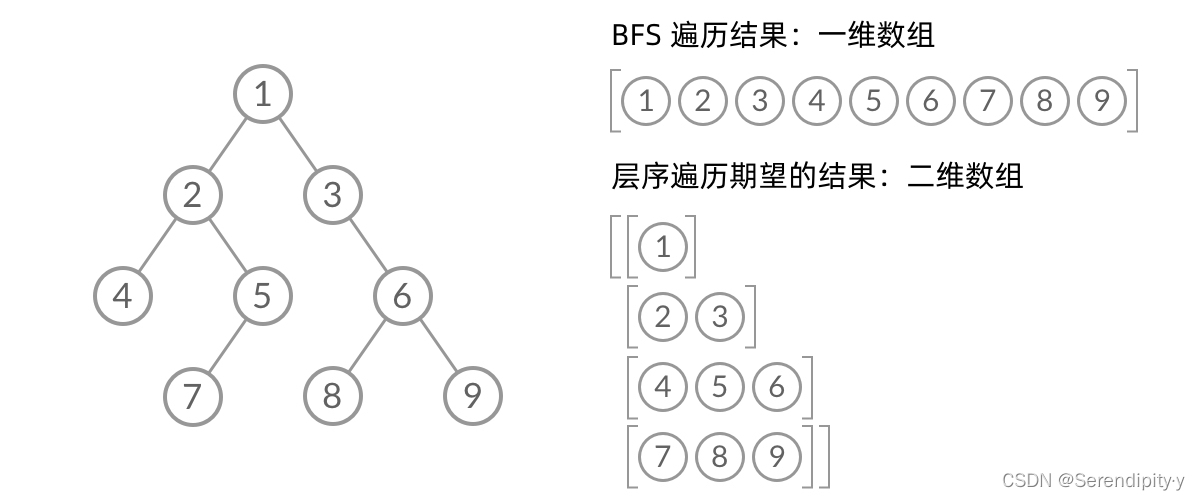
- 那么怎么给 BFS 遍历的结果分层呢?首先来观察一下 BFS 遍历的过程中,结点进队列和出队列的过程:
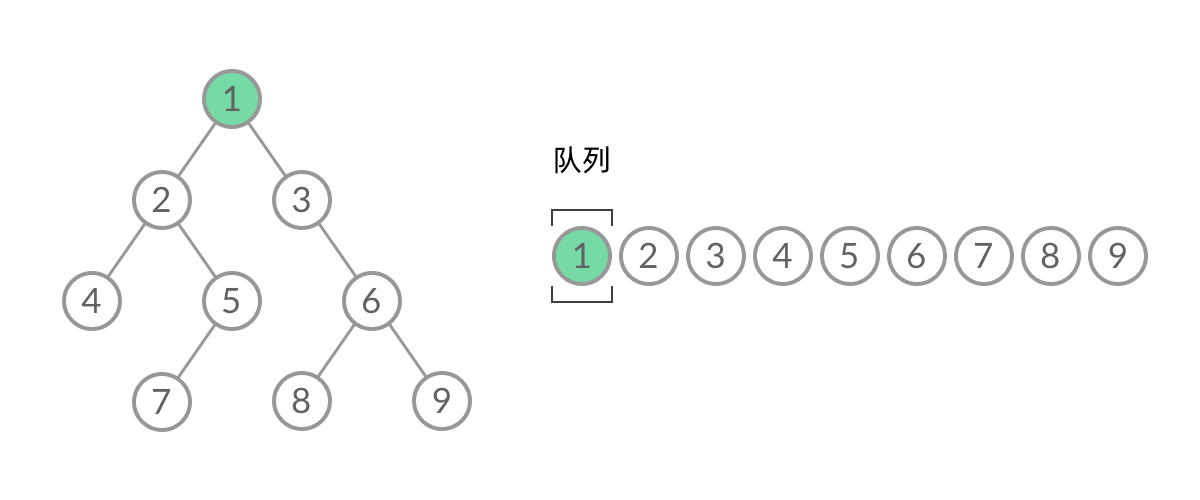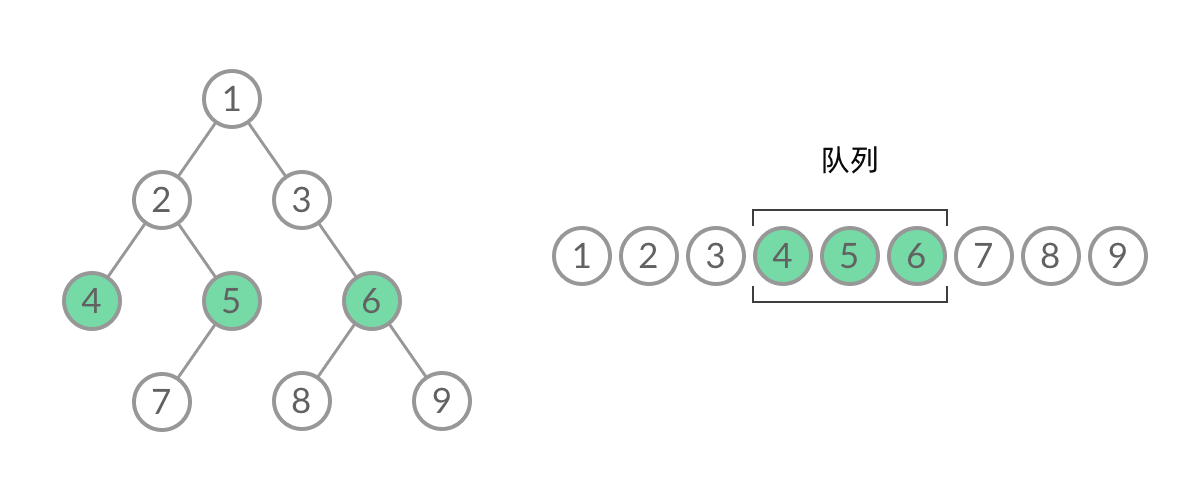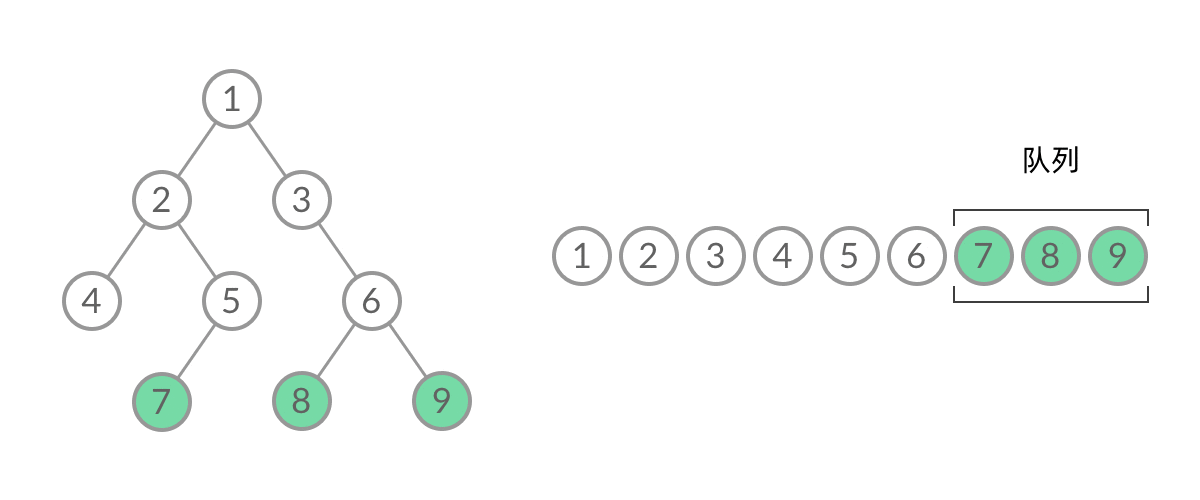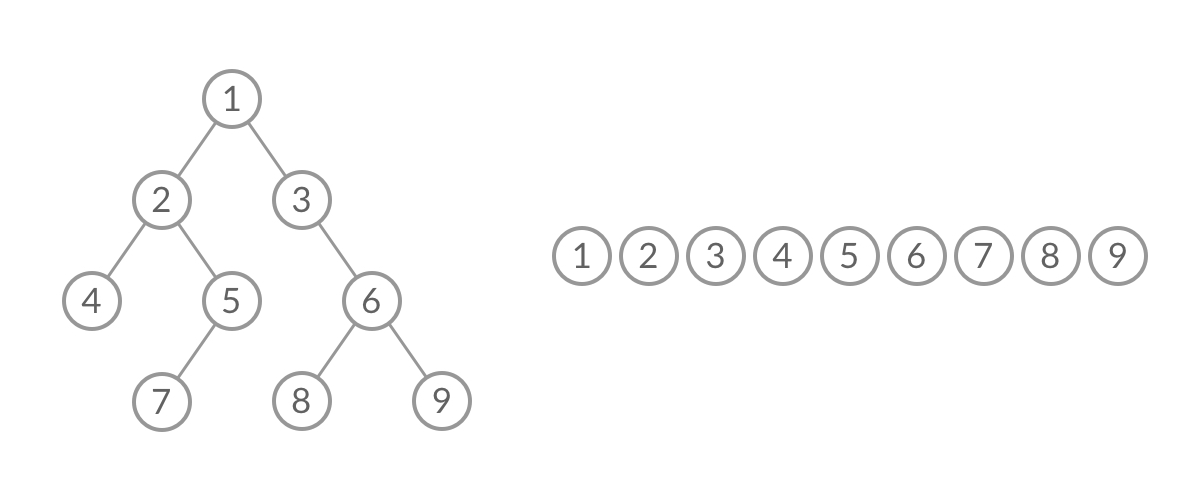
- 截取 BFS 遍历过程中的某个时刻:
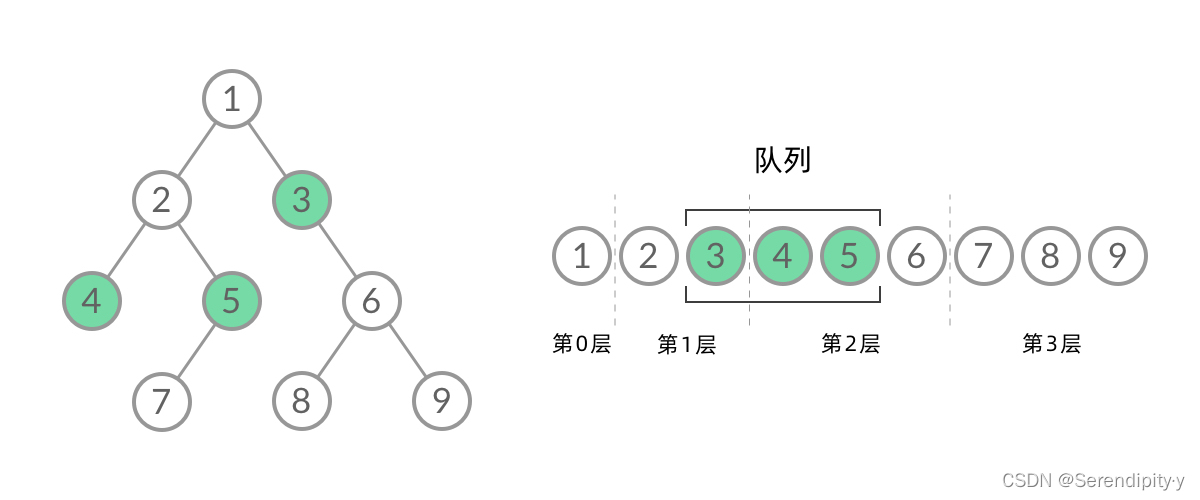
- 可以看到,此时队列中的结点是 3、4、5,分别来自第 1 层和第 2 层,这个时候,第 1 层的结点还没出完,第 2 层的结点就进来了,而且两层的结点在队列中紧挨在一起,我们无法区分队列中的结点来自哪一层。因此,需要稍微修改一下代码,在每一层遍历开始前,先记录队列中的结点数量 n(也就是这一层的结点数量),然后一口气处理完这一层的 n 个结点:
// 二叉树的层序遍历
void bfs(TreeNode root) {
Queue<TreeNode> queue = new ArrayDeque<>();
queue.add(root);
while (!queue.isEmpty()) {
int n = queue.size();
for (int i = 0; i < n; i++) {
// 变量 i 无实际意义,只是为了循环 n 次
TreeNode node = queue.poll();
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 这样就将 BFS 遍历改造成了层序遍历,在遍历的过程中,结点进队列和出队列的过程为:
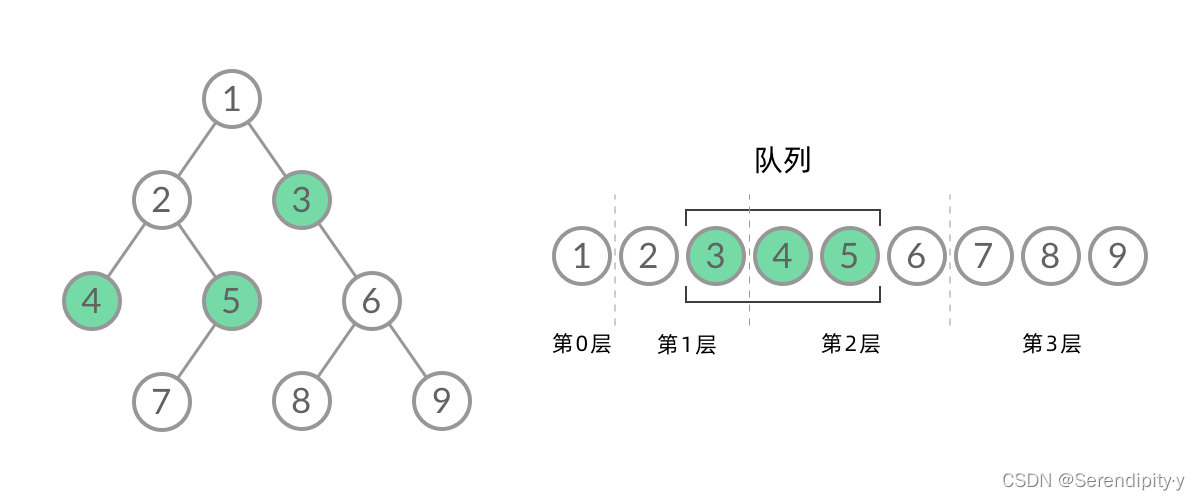
- 可以看到,在 while 循环的每一轮中,都是将当前层的所有结点出队列,再将下一层的所有结点入队列,这样就实现了层序遍历。
- Java 示例:
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
Queue<TreeNode> queue = new ArrayDeque<>();
if (root != null) {
queue.add(root);
}
while (!queue.isEmpty()) {
int n = queue.size();
List<Integer> level = new ArrayList<>();
for (int i = 0; i < n; i++) {
TreeNode node = queue.poll();
level.add(node.val);
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
res.add(level);
}
return res;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- Python 示例:
class Solution(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if not root:
return []
res = []
queue = [root]
while queue:
# 获取当前队列的长度,这个长度相当于 当前这一层的节点个数
size = len(queue)
tmp = []
# 将队列中的元素都拿出来(也就是获取这一层的节点),放到临时list中
# 如果节点的左/右子树不为空,也放入队列中
for _ in xrange(size):
r = queue.pop(0)
tmp.append(r.val)
if r.left:
queue.append(r.left)
if r.right:
queue.append(r.right)
# 将临时list加入最终返回结果中
res.append(tmp)
return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 在一棵树中,一个结点到另一个结点的路径是唯一的,但在图中,结点之间可能有多条路径,其中哪条路最近呢?这一类问题称为最短路径问题。最短路径问题也是 BFS 的典型应用,而且其方法与层序遍历关系密切。
- 在二叉树中,BFS 可以实现一层一层的遍历,在图中同样如此。从源点出发,BFS 首先遍历到第一层结点,到源点的距离为 1,然后遍历到第二层结点,到源点的距离为 2…… 可以看到,用 BFS 的话,距离源点更近的点会先被遍历到,这样就能找到到某个点的最短路径:
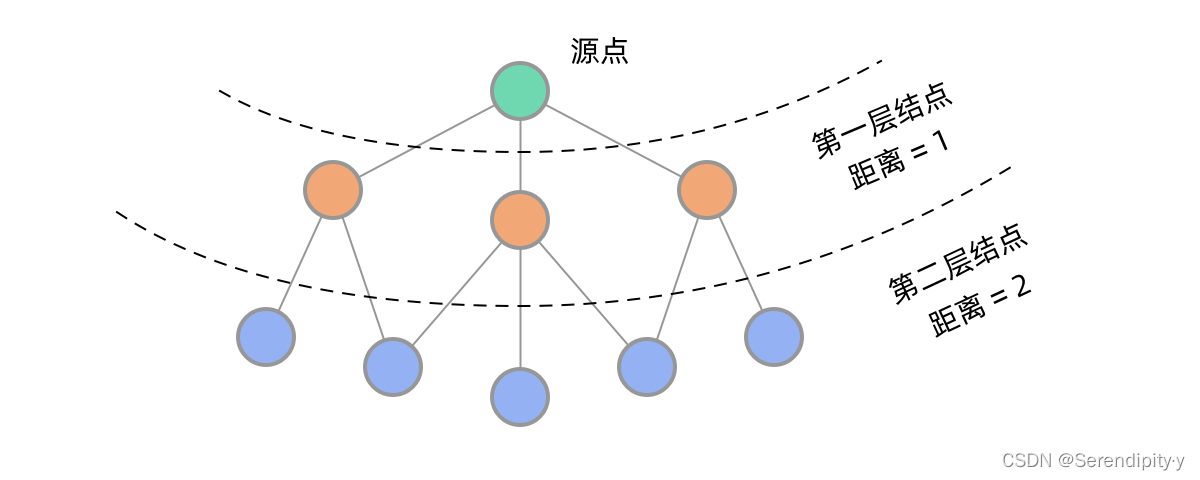
- 最短路径问题属于图算法,由于图的表示和描述比较复杂,可以用比较简单的网格结构代替,网格结构是一种特殊的图,它的表示和遍历都比较简单。
② 递归
- 用 BFS 处理是很直观的,可以想象成是一把刀横着切割了每一层,但是深度优先遍历就不那么直观:
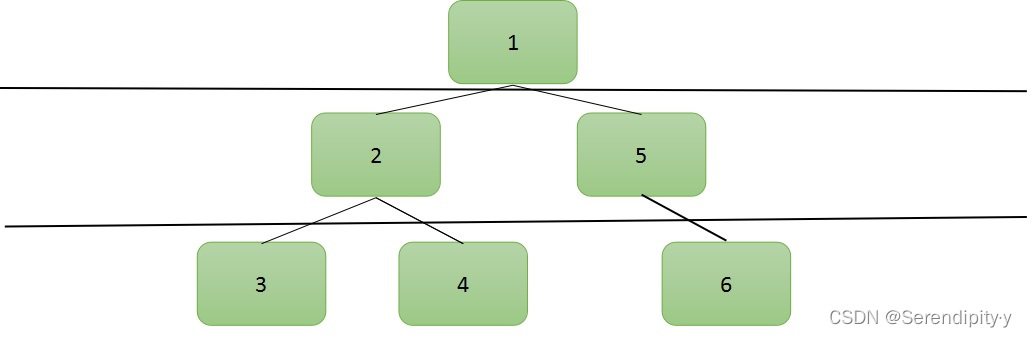
- 把这个二叉树的样子调整一下,摆成一个田字形的样子,田字形的每一层就对应一个 list:
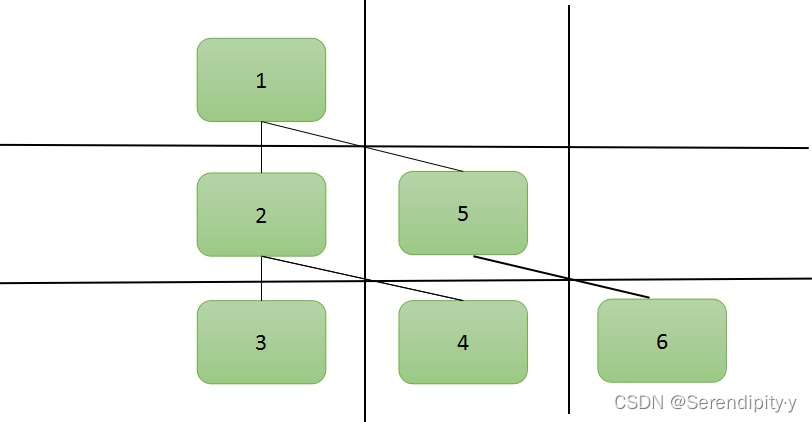
- 按照深度优先的处理顺序,会先访问节点 1,再访问节点 2,接着是节点 3;之后是第二列的 4 和 5,最后是第三列的 6。
- 每次递归的时候都需要带一个 index(表示当前的层数),也就对应那个田字格子中的第几行,如果当前行对应的 list 不存在,就加入一个空 list 进去。
- Java 示例:
import java.util.*;
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
if(root==null) {
return new ArrayList<List<Integer>>();
}
// 用来存放最终结果
List<List<Integer>> res = new ArrayList<List<Integer>>();
dfs(1,root,res);
return res;
}
void dfs(int index,TreeNode root, List<List<Integer>> res) {
// 假设res是[ [1],[2,3] ], index是3,就再插入一个空list放到res中
if(res.size()<index) {
res.add(new ArrayList<Integer>());
}
// 将当前节点的值加入到res中,index代表当前层,假设index是3,节点值是99
// res是[ [1],[2,3] [4] ],加入后res就变为 [ [1],[2,3] [4,99] ]
res.get(index-1).add(root.val);
// 递归的处理左子树,右子树,同时将层数index+1
if(root.left!=null) {
dfs(index+1, root.left, res);
}
if(root.right!=null) {
dfs(index+1, root.right, res);
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- Python 示例:
class Solution(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if not root:
return []
res = []
def dfs(index,r):
# 假设res是[ [1],[2,3] ], index是3,就再插入一个空list放到res中
if len(res)<index:
res.append([])
# 将当前节点的值加入到res中,index代表当前层,假设index是3,节点值是99
# res是[ [1],[2,3] [4] ],加入后res就变为 [ [1],[2,3] [4,99] ]
res[index-1].append(r.val)
# 递归的处理左子树,右子树,同时将层数index+1
if r.left:
dfs(index+1,r.left)
if r.right:
dfs(index+1,r.right)
dfs(1,root)
return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
三、拓展
- 如果将题目的要求变为“给你二叉树的根节点 root ,返回其节点值自底向上的层序遍历(即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)”,那么该怎么求解呢?
- 树的层次遍历可以使用广度优先搜索实现,从根节点开始搜索,每次遍历同一层的全部节点,使用一个列表存储该层的节点值。
- 如果要求从上到下输出每一层的节点值,做法是很直观的,在遍历完一层节点之后,将存储该层节点值的列表添加到结果列表的尾部。这道题要求从下到上输出每一层的节点值,只要对上述操作稍作修改即可:在遍历完一层节点之后,将存储该层节点值的列表添加到结果列表的头部。
- 为了降低在结果列表的头部添加一层节点值的列表的时间复杂度,结果列表可以使用链表的结构,在链表头部添加一层节点值的列表的时间复杂度是 O(1)。在 Java 中,由于需要返回的 List 是一个接口,这里可以使用链表实现;而 C++ 或 Python 中,我们需要返回一个 vector 或 list,它不方便在头部插入元素(会增加时间开销),所以我们可以先用尾部插入的方法得到从上到下的层次遍历列表,然后再进行反转。
- Java 示例:
class Solution {
public List<List<Integer>> levelOrderBottom(TreeNode root) {
List<List<Integer>> levelOrder = new LinkedList<List<Integer>>();
if (root == null) {
return levelOrder;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> level = new ArrayList<Integer>();
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
level.add(node.val);
TreeNode left = node.left, right = node.right;
if (left != null) {
queue.offer(left);
}
if (right != null) {
queue.offer(right);
}
}
levelOrder.add(0, level);
}
return levelOrder;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- C++ 示例:
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
auto levelOrder = vector<vector<int>>();
if (!root) {
return levelOrder;
}
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
auto level = vector<int>();
int size = q.size();
for (int i = 0; i < size; ++i) {
auto node = q.front();
q.pop();
level.push_back(node->val);
if (node->left) {
q.push(node->left);
}
if (node->right) {
q.push(node->right);
}
}
levelOrder.push_back(level);
}
reverse(levelOrder.begin(), levelOrder.end());
return levelOrder;
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
文章来源: blog.csdn.net,作者:Serendipity·y,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/Forever_wj/article/details/122969458
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)